Inscription / Connexion Nouveau Sujet
Etude de la charge d'un condensateur
Bonjour, pouvez-vous m'aider ? merci d'avance.
Exercice:
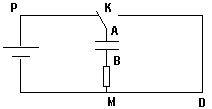
Le générateur PM possède une f.e.m.E.Sa résistance interne est négligeable.
1)a) A la date t=0s, on relie K à P.Montrer que l'équation différentielle reliant UAB à t s'écrit:
RC dUAB/dt + UAB = E ou encore : 
*dUAB/dt + UAB = E en posant = RC.
Montrer que, dans le système international d'unités, la constante s'exprime en seconde.
b) Vérifier que la solution de l'équation différentielle ci-dessus est : UAB = E [1-exp(-t/)].
c)Tracer l'allure de la courbe représentant UAB = E [1-exp(-t/)].Déterminer littéralement les coordonnées du point d'intersection de la tangente à l'origine et de l'asymptote à la courbe.
d) Calculer la constante de temps du circuit = RC avec R=10 k
et C = 0.5 microF.
Calculer la tension UAB aux dates t1= , t2=5 et lorsque t devient très grand.On donne E=100V.
2)a) Le condensateur étant chargé, on relie K à D à la date t=0 lue sur un nouveau chronomètre.
Etablir la nouvelle équation différentielle reliant UAB à t.
b) vérifier que la solution est UAB = Uo exp (-t/).Calculer la tension si t1=o, si t2=5, si t tend vers l'infini.
Mes réponses:
1)a)La loi des mailles s'écrit :
uPA + uAB + uBM + uMP = 0
le générateur PM possède une f.e.m.E. Donc, uPM = E >0.
Ainsi, uPA + uAB + uBM + uMP = 0
0 + uAB + R iBM - E = 0.
uBM = R*i BM.
De plus, l'intensité dans un circuit en série est la même partout. Donc, iBM=iAB.
Or, iAB= dqA/dt. qA = C * uAB.
iAB= C* duAB/dt.
Donc, uAB + RC duAB / dt = E.
=RC. Ainsi, uAB+*duAB/dt= E.
Montrer que, dans le système international d'unités, la constante s'exprime en seconde?
Salut,
1) D'après la loi des mailles on a : E = Uab + Ubm
<=> E = Uab + R.i
<=> E = Uab + R.C.(dUab/dt) car i = c.(du/dt) pour un condensateur alimenté par une tension u
Donc R.C(dUab/dt) + Uab = E
<=> (dUab/dt) + Uab/R.C = E/R.C , en posant = R.C
<=> dUab/dt + Uab/ = E
On fait une analyse dimensionnelle s'exprime en Farad * Ohm or des Ohm d'après la loi d'Ohm s'exprime par une tension sur un courant et des farad par une charge q multipliè par une tension, d'après i=dq/dt on abien qui s'exprime comme un temps dans le système S.I
2) On résout l'équa diff : la solution est de la forme :
Uab(t) = K.exp(-t/)+ E
Conditions initiales : on suppose le condenstaur déchargé d'où Uab(0)=0 donc on trouve K = -E
d'où la solution finale Uab(t) = E ( 1 - exp ( -t/)
3) Pour la courbe prendre une calculette !!
Bonne continuation !!
Annuler
connectez vous