Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Espace parcouru.

Posté par
kamikaz 25-12-20 à 18:29

Bonsoir ,

Joyeux Noël et merci d'avance.

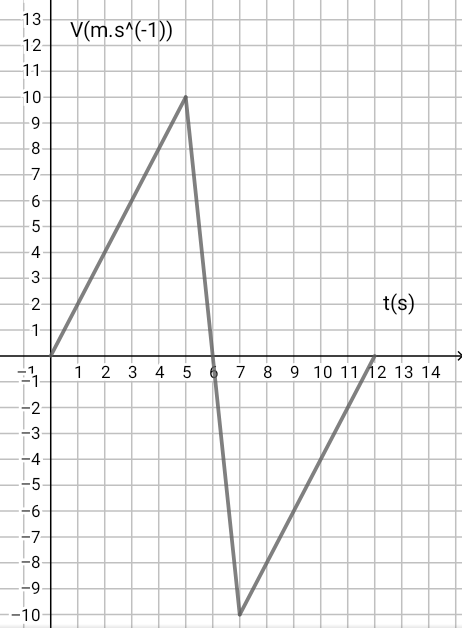
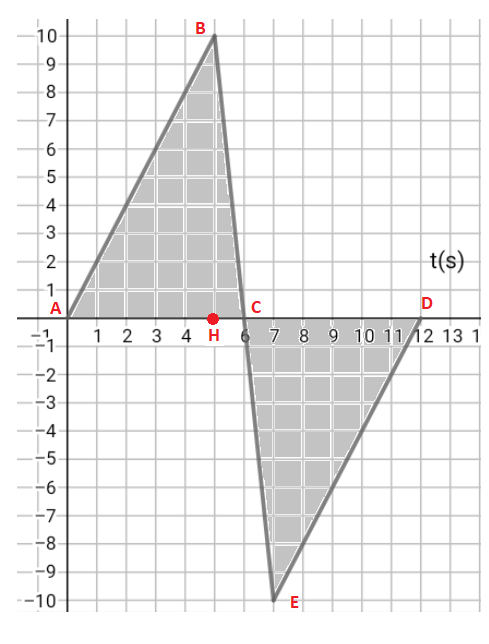
Espace parcouru.

La représentation graphique de la vitesse V=f(t) d'un automobile est donné par la figure ci-dessus.

1) Calculer les accélérations du mobile au cours des trois phases.

2) Calculer l'espace parcouru par le mobile.

Réponses

1) a_{i}=\dfrac{V_{f}-V_{i}}{t_{f}-t_{i}} .

t\in [0 ;5s] , a_{1}=\dfrac{10-0}{5-0}=2 m/s²

t\in [5;7] , a_{2}=\dfrac{-10-10}{7-5}=-10m/s²

t\in [7;12] , a_{3}=\dfrac{0+10}{12-7}=2m/s²


2) Je ne comprends pas très bien..

Est ce que je dois calculer une aire ou une distance ?

Posté par
odbugt1re : Espace parcouru. 25-12-20 à 18:41

Bonjour,

Tu dois calculer une distance, mais il se trouve que cette distance est égale à l'aire (arithmétique) comprise entre l'axe des temps et la "courbe" v(t)

Posté par
kamikazre : Espace parcouru. 25-12-20 à 18:51

Ah çà alors..

Tu pourrais détailler un peu , c'est un peu flou là

Posté par
odbugt1re : Espace parcouru. 25-12-20 à 19:06

L'aire de chaque carreau représente le produit d'une vitesse de 1m/s par une durée de 1s ce qui revient à dire que l'aire de chaque carreau représente une distance parcourue de (1m/s * 1s) = 1m
En dénombrant les carreaux compris entre l'axe des temps et la courbe tu obtiens du même coup la distance parcourue.

Bien entendu, tu peux aussi (ce sera plus long) calculer la distance parcourue à l'aide des équations classiques des mouvements uniformément variés .

Posté par
vanoisere : Espace parcouru. 25-12-20 à 19:47

Bonsoir
Juste un détail à propos de l'aire de chaque triangle  : pourquoi ne pas tout simplement calculer le demi produit de la hauteur par la base ?

Posté par
kamikazre : Espace parcouru. 25-12-20 à 20:07

Citation :
Bien entendu, tu peux aussi (ce sera plus long) calculer la distance parcourue à l'aide des équations classiques des mouvements uniformément variés .


Soit x_{1}=\dfrac{1}{2}a_{1}t²+V_{0}t+x_{0}=\dfrac{1}{2}a_{1}t²=t²  l'équation horaire du mobile lors de la 1ère phase.

x_{2}=\dfrac{1}{2}a_{2}t²+V_{5}t+x_{5}=-5t²+10t+5\sqrt{5} l'équation horaire du mobile lors de la 2ème phase.

x_{3}=\dfrac{1}{2}a_{3}t²+V_{7}t+x_{7}=t²-10t+\sqrt{149} l'équation horaire du mobile lors de la 3ème phase.

Je fais comment ensuite ?

Posté par
odbugt1re : Espace parcouru. 25-12-20 à 21:02

@Vanoise
Dans mon esprit, le dénombrement dont je parle consistait en effet à faire le calcul que tu évoques.

@kamikaz
Phase 1 : De t=0 à t=5s :
Le plus simple est d'appliquer : (v(5))² - (v(0))² = 2*a1*D1
D1 est la distance parcourue pendant cette phase.
v(5)= 10 m/s
v(0) = 0 m/s
a1 = 2 m/s²
Donc D1 = ...............

Phase 2 : De t=5s à t=6s
Je te laisse faire pour trouver D2 ( distance parcourue pendant cette phase)

Phase 3 : De t=6s à t = 12s
Compte tenu de la symétrie du mouvement la distance parcourue pendant cette phase est égale à D1 + D2

Mais franchement je préfère l'autre méthode qui permet d'obtenir le résultat cherché par un simple calcul mental.

Posté par
odbugt1re : Espace parcouru. 25-12-20 à 21:09

Remarque :
Les phases ( 1 , 2 3 ) que j'ai utilisées ne sont pas les mêmes que celles définies à la question 1 de l'énoncé

Posté par
kamikazre : Espace parcouru. 25-12-20 à 21:33

En utilisant cette méthode , ça va faire l'espace E=10-10+10-10=0..

Je trouve ça bizarre..

Voilà pourquoi je veux faire avec l'autre méthode.

Posté par
odbugt1re : Espace parcouru. 25-12-20 à 22:02

Désolé, mais je ne comprends pas de quoi tu parles.
Comment obtient tu  ton curieux 10 - 10 + 10 -10 ?
Parce que moi aussi, je trouve ça bizarre !

Posté par
kamikazre : Espace parcouru. 25-12-20 à 23:01

Ben en comptant les carreaux ..

Dans la partie négative il y a 10 donc -10 et 10 dans la positive donc 10 ( pour chaque phase..)

Posté par
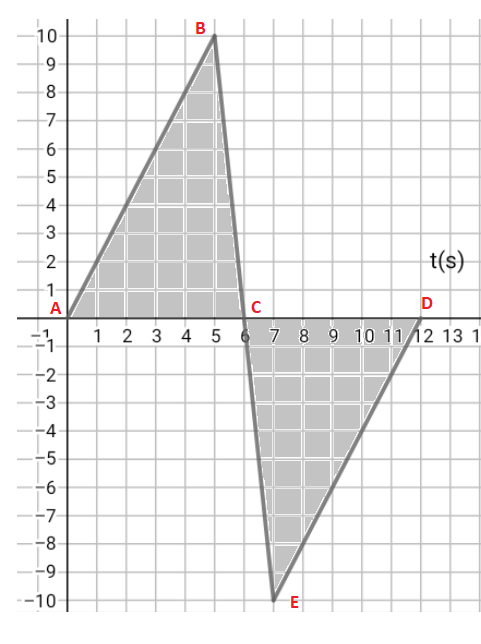
odbugt1re : Espace parcouru. 26-12-20 à 00:01


Compter les carreaux de la partie grise du schéma ci-dessous n'est pas directement possible puisque beaucoup d'entre eux ne sont pas entiers.

On contourne cette difficulté en calculant la somme des aires (positives) des triangles ABC et CDE. Voir si nécessaire le message de Vanoise (25-12-20 à 19:47)

Cette aire correspond à la distance cherchée.

Espace parcouru.

Posté par
gts2re : Espace parcouru. 26-12-20 à 08:32

Bonjour,

Juste une remarque de vocabulaire, j'ai l'impression que kamikaz a compris déplacement (qui est bien nul) à la place de distance.

Posté par
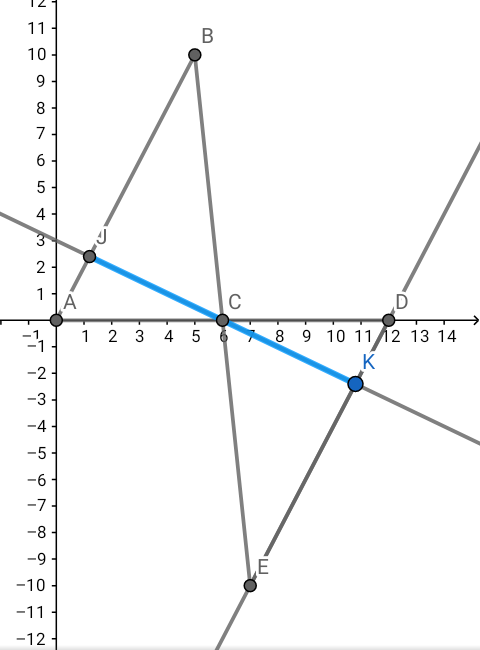
kamikazre : Espace parcouru. 26-12-20 à 09:05

OK ,

Espace parcouru.

Alors j'ai déterminé l'aire du triangle CDE et ensuite remarqué que les distances AB et ED ; AC et CD ; BC et CE sont respectivement égales.

Donc les aires des triangles ABC et CDE sont égales.

D'où l'espace parcouru \boxed{E=2×A_{\text{aire CDE}}}

* Déterminer les coordonnées du point K , intersection des droites (CK) et (ED).

. Équation de (JK) ou (CK).

[CK] étant la hauteur de CDE , K \in [ED] avec K(x;y).

\vec{CK} et \vec{ED} sont orthogonaux c'est à dire \vec{CK}.\vec{ED}=0

C(6 ; 0) , E(7 ; -10) et D(12 ; 0)

==> \vec{CK}(x-6 ; y) et \vec{ED}(5 ; 10)

Donc \vec{CK}.\vec{ED}=0 \iff 5(x-6)+10y=0

\iff 5x-30+10y=0

\iff 5x+10y-30=0

\iff x+2y-6=0

Donc (CK) : x+2y-6= 0

. Équation de (ED)

K \in (ED)

Donc \vec{EK} et \vec{ED} sont colinéaires.

\vec{EK}(x-7 ;y+10) et \vec{ED}(5;10)

==> 10(x-7)-5(y+10)=0

10x-5y-120=0

2x-y-24=0

Donc (ED) : 2x-y-24=0

On a : (CK) : 5x+10-30=0

(ED) : 2x-y-24=0

K = (ED) \cap (CK)

Donc pour déterminer ses coordonnées , on résoud le système :

\begin{cases} y=\dfrac{30-5x}{10} \\ y= 2x-24 \end{cases}

\begin{cases} 2x-24=\dfrac{30-5x}{10} \\ y= 2x-24 \end{cases}

\begin{cases} 25x=270 \\ y= 2x-24 \end{cases}

\begin{cases} x=\dfrac{54}{5} \\ y= -\dfrac{12}{5} \end{cases}

==> K(\dfrac{54}{4} ;-\dfrac{12}{5})

CK est la distance du point C à la droite (ED).

Donc CK=\dfrac{|2×(6)-0-24|}{\sqrt{2²+(-1)²}}=\dfrac{12\sqrt{5}}{5}

D'où CK=\dfrac{12\sqrt{5}}{5}

La base ED du triangle CDE est : ED=\sqrt{5²+10²}=5\sqrt{5}

==> A_{CDE}=\dfrac{1}{2}×\dfrac{12\sqrt{5}}{5}×5\sqrt{5}=30

A_{CDE}=30 m²

==> E= 2×30 = 60 m²

E= 60 m²

Donc le mobile a parcouru une superficie de 60 m².

Posté par
kamikazre : Espace parcouru. 26-12-20 à 09:18

gts2 @ 26-12-2020 à 08:32

Bonjour,

Juste une remarque de vocabulaire, j'ai l'impression que kamikaz a compris déplacement (qui est bien nul) à la place de distance.


Exactement , mais je n'arrive pas à montrer que ça fait 0 par les calculs.. Tu pourrais le faire s'il te plaît..

Posté par
mmalou Webmasterre : Espace parcouru. 26-12-20 à 09:30

Bonjour à tous, je ne fais que passer...
kamikaz, je viens te tirer les oreilles pourquoi faire simple quand on peut faire compliqué n'est-ce pas ? ...choisis d'autres bases pour tes triangles !

Posté par
odbugt1re : Espace parcouru. 26-12-20 à 09:36

Le mobile au bout de 12s est revenu à son point de départ.
Son déplacement est donc nul, mais la distance qu'il a parcourue ne l'est pas.

Le calcul de l'aire du triangle ABC est grandement simplifié en utilisant :
Aire = (1/2) * AC *  BH = (1/2) * 6 * 10 = 30
L'aire totale est donc de 60 unités " carreaux"
Chaque carreau représente une distance parcourue de 1m (voir 25-12-20 à 19:06)

Distance parcourue = 60m

Espace parcouru.

Posté par
kamikazre : Espace parcouru. 26-12-20 à 11:11

Ah oui

J'aurais dû utiliser l'autre figure (celle avec les carreaux)..

Merci

Posté par
odbugt1re : Espace parcouru. 26-12-20 à 11:55

A titre indicatif je te joins un graphique donnant la distance parcourue ( et non l'abscisse ) du mobile en fonction du temps.

Espace parcouru.

Posté par
kamikazre : Espace parcouru. 26-12-20 à 12:03

Comment l'obtenez vous ?

Posté par
odbugt1re : Espace parcouru. 26-12-20 à 12:27

Entre 0 et 7s à: A partir de l'abscisse du mobile
Entre 7 et 14s : Par symétrie

Posté par
odbugt1re : Espace parcouru. 26-12-20 à 12:34

Pardon ....
Entre 0 et 6s :  A partir de l'abscisse du mobile
Entre 6 et 12s : Par symétrie

Posté par
kamikazre : Espace parcouru. 26-12-20 à 13:40

OK

Merci


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !