Inscription / Connexion Nouveau Sujet
Equilibre
Bonjour,
Pouvez-vous m'aider s'il vous plait ?
On suppose que la situation est à l'équilibre. On néglige les frottements, ainsi que les poids des fils et des blocs 4 et 5. Les charges ont une masse m1=6kg, m2=10kg et m3=8kg. Il faut trouver, par rapport à la verticale, l'angle où sont disposées les sections des fils DE et EF. On prendra g=10m/s².

PDF - 5 Ko
Bonsoir
Le plus simple consiste à écrire que la résultante vectorielle des trois forces appliquées en E est le vecteur nul.
Les poulies se comportent en simple transmetteurs d'efforts : elle modifient les directions et sens des forces sans en modifier les intensités.
Tu peux faire un schéma propre où les vecteurs forces sont représentés puis projeter la relation vectorielle sur deux axes à préciser.
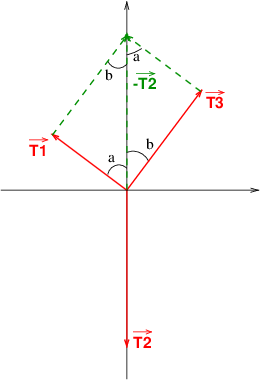
On prend un repère (x,y) placé au point E. A gauche de l'axe y, on a l'angle (a), et à droite de cet axe, on a l'angle (b). On a une tension 1 qui va vers le point D et une tension 2 qui va vers le point F. Est-ce que les composantes des tensions sont celles-ci ?
T1 x = -T1*sin(a)
T1 y = T1*cos(a)
T2 x = T2*sin(b)
T2 y = T2*cos(b)
Ton idée est bonne. Il serait bon de compléter le schéma. Compte tenu de la figure déjà faite, il serait plus logique de noter T1 et T3 les tensions obliques et de noter T2 la tension verticale orientée vers le bas. Tu peux compléter ton schéma avec les vecteurs forces, le poster ici, puis écrire le système de deux équations à deux inconnues et le résoudre...
1° : Comme déjà dit, il me semble plus logique de faire correspondre aux indices des masses, les indices correspondant des tensions : à la masse m1 correspond la tension T1, à la masse m2 correspond la tension T2...
2° : la valeur de g (surtout grossièrement arrondie comme ici...) n'est pas utile au problème car des simplifications par g interviennent dans les calculs.
3° : la méthode de projection déjà indiquée est la méthode la plus générale et peut être appliquée ici. Dans ce cas très particulier, on peut faire un peu plus rapide en pensant au théorème de Pythagore et en remarquant :
m22=m12 + m32
Cela veut dire que T1=m1g, -T2=m2g et T3=m3g ?
Je ne comprends pas comment on arrive à (m2)²=(m1)²+(m3)².
Cela veut dire que T1=m1g, -T2=m2g et T3=m3g ?
oui si T2=T2y ; Si T2 désigne la norme du vecteur : T2=m2.g...
Je ne comprends pas comment on arrive à (m2)²=(m1)²+(m3)².
Cela n'est pas le cas général. Juste un cas très particulier choisi par le concepteur de l'énoncé pour éventuellement faciliter la résolution du problème. Tu peux facilement vérifier :
102=62 + 82
Partant de l'égalité précédente puis en multipliant par g2, cela conduit à :
Que dire alors du parallélogramme résultant de la relation vectorielle :
(Penser au théorème de Pythagore)
Problème de signe déjà signalé. Les cosinus font intervenir le rapport de deux normes de vecteurs donc des rapports de grandeurs positives.
On a donc T1=m1*g ; T2=m2*g et T3=m3*g. Est-ce que -T2 = m2*g ou -m2*g ? Doit-on mettre des vecteurs au-dessus de T1, T2, T3 et g, ou laisser sans flèche ?
La convention la plus courante dans ce genre d'exercice consiste à désigner la norme d'un vecteur par le symbole du vecteur auquel la flèche est enlevée.
Par exemple, on note T2 à la place de . Or, une norme de vecteur est toujours positive. Donc ici :
T1=m1*g ; T2=m2*g et T3=m3*g.


