Inscription / Connexion Nouveau Sujet
Equations horaires
On considère un système de masse m = 1,0*102 kg composé d'un cycliste et de son vélo. Le système, roulant à une vitesse V0 = 10 m.s-1, freine sur une route horizontale à partir de l'instant t = 0s. Il est à l'arrêt au bout de 5,0 m. On négligera l'action de l'air et on notera F ( vecteur la force de frottement du sol, de norme F constante.
1. Faire le bilan des forces appliquées sur le système.
Force de frottement F (vecteur) + poids P (vecteur) + réaction du sol sur le vélo R (vecteur).
2. A l'aide de la 2 ème loi de Newton, determiner les équations horaires de la vitesse et de la position du système, en fonction de F, m, V0 et du temps t .
On étudie le mouvement du système [cycliste/vélo] dans le réferentiel terrestre, suposé galiléen.
Conditions initiales :
C'est dès la que je bloque....
Merci de votre aide ! 
Bonjour,
Je t'invite à lire attentivement cette fiche : 
Statique et dynamique - Les lois de Newton
Il faudrait que tu commences la deuxième question avec un schéma de la situation sur lequel le systèmes et ses forces appliquées seront représentées ainsi que le repère de l'étude.
Bonjour,
1) oui
2) oui, et une fois choisi le referentiel, il faut definir un repere: on peut supposer qu'à t=0 le systeme est en O (origine du repere) et se deplace selon l'axe (O,x)
(Il faut faire un dessin)
,
Bonjour @krinn.
Merci de votre réponse.
Donc,
on aurais :
OM (vecteur) (0) :
- x(0) = 0
- y(0) = d (ici d serais la distance)
V (vecteur) (0) :
- x(0) = 0
- y(0) = 10
Je ne sais pas comment representer le shema si ce quej'ai fais n'est pas bon...
Bonjour,
Ici le mouvement est rectiligne, une seule coordonnee suffit pour reperer le point.
(Voir figure)
Donc si M est en O à t=0, on a x(0) = ....
Et Vx(0) = ...
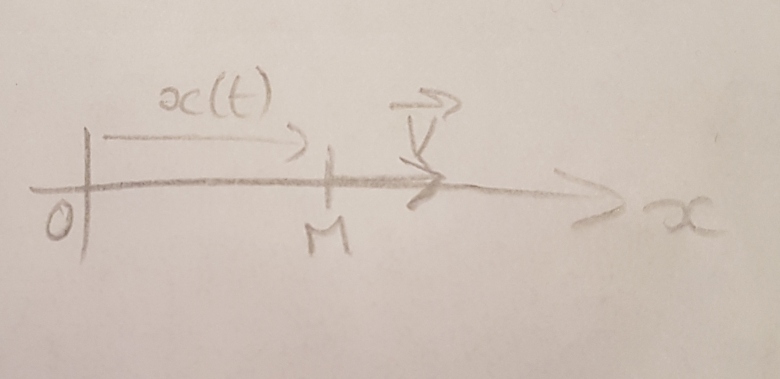
Et après cela, il faut faire l'accélération donc on a :
la somme de F (vecteur) = m*a (vecteur)
On peut retrouver le poids avec la formule P=mg
on trouve P= 9,81_10² N
Il nous faut donc R. Comment le trouve t-on ? avec la 3eme loi de Newton ?
Oui, V(0) = Vo
Il faut faire un dessin avec les forces:
P
R
et ....
Donc P+R+ ... = m a
(vecteurs en gras)
Et comme le mouvement est rectiligne, on projette sur (O,x)
Annuler
connectez vous