Inscription / Connexion Nouveau Sujet
Equation différentielle Electricité
Bonsoir tout le monde , je n'arrive pas à résoudre cet exercice ( c'est un devoir maison à rendre pour demain ) , si quelqu'un pourrait m'aider:
Ecrire l'équation différentielle qui régit le circuit RLC en prenant comme variable temporelle ULr (t) .
Salut,
Si tu commençais à relire les éléments du cours, ça pourrait t'aider :
Oscillations libres dans un circuit RLC
Oui , je connais mon cours, mais je n'arrive pas à trouver l'équation en fonction de Ulr. Auriez vous une indication ?
Tu ne définis pas tes notations ...
Ulr c'est la tension aux bornes de la bobine idéale ? De la bobine en tenant compte de sa résistance interne ?
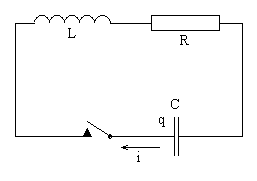
As-tu un schéma du circuit ?
On dérive :
Or et
donc
on dérive une deuxième fois :
sachant que
A relire, on n'est jamais à l'abri d'une erreur d'inattention.
et donc il y a à chaque fois un i dont on ne peut se débarrasser ?
Ben si ...
Ubob = L di/dt + r.i (1)
Ubob + R.i + Uc = 0 (équation de la maille).
avec i = C.dUc/dt
dUbob/dt + R di/dt + i/C = 0
dUbob/dt + (R/L).(Ubob - ri) + i/C = 0
dUbob/dt + (R/L).Ubob + i.(1/C - Rr/L) = 0
i = (dUbob/dt + (R/L).Ubob)/(Rr/L - 1/C)
dans (1) -->
Ubob = L/(Rr/L - 1/C) * (d²Ubob/dt + (R/L).dUbob/dt) + r.(dUbob/dt + (R/L).Ubob)/(Rr/L - 1/C)
(Rr/L - 1/C).Ubob = L * (d²Ubob/dt + (R/L).dUbob/dt) + r.(dUbob/dt + (R/L).Ubob)
L * d²Ubob/dt + (R+r) * dUbob/dt + (Rr/L - Rr/L + 1/C) * Ubob = 0
L * d²Ubob/dt + (R+r) * dUbob/dt + (1/C) * Ubob = 0
d²Ubob/dt + ((R+r)/L) * dUbob/dt + (1/(LC)) * Ubob = 0
----
Pas vérifié.
Annuler
connectez vous