Inscription / Connexion Nouveau Sujet
Equation différentielle - dipôle RLC
Bonjour,
J'ai un problème avec la fin d'un exercice type BAC de physique sur RC, RL et RLC.
C'est la dernière question de l'exo : "Etablir l'équation différentielle qui régit l'évolution de Uc au cours du temps"
Le condensateur est préalablement chargé ( interrupteur en position 1). L'enregistrement des variations de la tension aux bornes du condensateur en fonction du temps commence quend on bascule l'interrupteur en position 2.
Le circuit est joint au post. Merci d'avance, c'est frustrant de bloquer sur la fin !
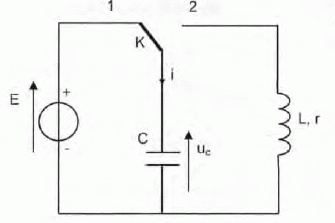
Donc, votre circuit se résume, au déclenchement du chrono, à un condensateur chargé en série avec une bobine d'impédance L et de résistance r.
Si on commençait par écrire la loi des mailles ?
uC + u(L;r) = 0
Or, u(L;r) = L.di(t)/dt + r.i(t)
De plus, i(t) = dq(t)/dt = d[C.uC(t)]/dt = C.duC(t)/dt
Et donc, si on dérive i(t) par rapport au temps
di(t)/dt = d( C.duC(t)/dt )/dt = C.d²uC(t)/dt²
On réinjecte le tout dans la loi des mailles :
uC + L.C.d²uC(t)/dt² + r.C.duC(t)/dt = 0
Ce qui, de manière ordonnée et plus 'normalisée', donne :
d²uC(t)/dt² + (r/L).duC(t)/dt + 1/(LC).uC = 0
- sauf distraction -
Ah oui, ça me dit quelque chose par rapport à ce que j'ai vu dans mon livre cette équation. Pas encore vu en cours pourtant, bizarre que ce soit demandé en exo ...
Mais merci pour tout !
Si l'exercice en question est tirée d'un annabac ou alors un exo type-bac donné par votre professeur...
Alors il a sûrement oublié d'ôter cette question si ce genre d'équation n'a pas encore traité en cours.
Ceci dit, c'est à votre portée... Cela ne demande que de connaître la loi des mailles, la dérivation mathématique (hormis le symbolisme d/dt plus propre à la physique) ainsi que les expressions des tensions aux bornes d'une bobine et d'un condensateur...
Bonne soirée !


