Bonjour,

Est ce que tu as un exercice que tu ne comprends pas, ça sera plus simple de t'aider avec un exemple. Les équations différentielles en maths ou en physique sont les mêmes, on écrit simplement en physique dv/dt que tu écrirais en maths v'(t).

Les équations différentielles se retrouvent dans beaucoup des domaines comme par exemple en mécanique dans l'étude des oscillateurs harmoniques car on fait intervenir l'accélération et la vitesse d'un objet dans une même équation donc on fait intervenir la vitesse et la dérivée de la vitesse ce qui est une équation différentielle.

La résolution des équations différentielles se passent comme en maths, on cherche la solution sans second membre et la solution particulière. Il faut parfois savoir traduire l'énoncé pour trouver les conditions initiales qui permettent de trouver la solution particulière.

Essaies de trouver un exercice qui te pose problème et on le fait ensemble comme ça on verra ce qui te bloque...

Merci pour cette réponse rapide

Alors voilà, un exemple d'exercice:

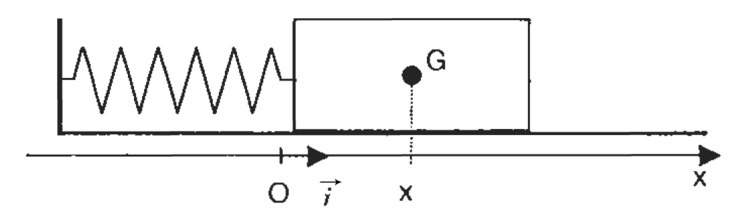
Un pendule élastique est constitué d'un mobile de masse m = 80 g pouvant se déplacer sur un banc à coussin d'air horizontal. Ce mobile est attaché à un point fixe par un ressort de masse négligeable à spires non jointives, de raideur k. La position du mobile est repérée par l'abscisse x sur l'axe (O,\vec{i}). À l'équilibre, la position du centre d'inertie G coïncide avec le point O, origine des abscisses.

I. Étude de l'oscillateur parfait (non amorti)

Dans cette partie, on considère que le mobile n'est soumis à aucune force de frottement.

1. Indiquer l'expression vectorielle de la force {F} de rappel du ressort en fonction de l'abscisse x du centre d'inertie du mobile et de {i} vecteur unitaire.

2. Faire l'inventaire des forces qui s'exercent sur le mobile. Reproduire le schéma ci-dessus et représenter ces forces.

3. À l'aide de la deuxième loi de Newton, établir l'équation différentielle du mouvement (relation entre l'abscisse x(t) et ses dérivées par rapport au temps).

4. Un dispositif d'enregistrement de la position x du mobile permet de mesurer la valeur T0 de la période du mouvement : T0 = 0,20 s.
Quelle est la valeur numérique de la raideur k du ressort sachant que
T0 = 2m/k  ?

Pour ce qui est de mes réponses:

1.l'Expression vectorielle de la force est:  F= -k*x*

2.L'inventaire des forces soumises sur le mobile sont: le poids, la réaction du support et la force de rappel.

3.à partir de là, dans mon esprit c'est un peu flou, donc voilà ce que j'ai fais:

F=m*a
            P+F+R=m*a
                F=m*a       (P+R=0 car on est sur un support)
             -k*x=m*a
             -k*x=m*(d²x/dt)
   d²x/dt + k*x/m=0         à partir de là, je sais plus faire

Merci cependant pour votre réponse rapide

Ok pour toutes les questions jusqu'à la 3.

Alors moi j'ai toujours fait avec une certaine méthode, je ne dit pas que ce que tu as fait est faux mais il manque la notion de vecteur dans les premières relations:

     a_G/R est simplement l'accélération du point G dans le repère R.

On a donc:

   je décompose l'expression pour voir quelle force agit suivant quel axe. ex=vecteur unitaire suivant l'axe x (c'est ton i) ; ey=vecteur unitaire suivant l'axe y (ça serait un j s'il était marqué sur le schéma mais on s'en fout ^^)

Donc on ne s'intéresse qu'à ce qui est suivant l'axe x, donc là on peut maintenant passer sous une expression scalaire (on ne tient plus compte des vecteurs car on travaille suivant le vecteur ex):

      avec           c'est juste une notation comme le x" en maths pour ne pas s'embêter avec la dérivée sous forme de fraction.

On développe l'expression de F:

Ce qui nous donne donc:

Je sais c'est bien ce que tu as trouvé mais c'était simplement pour montrer qu'il y a une notion de vecteur à prendre en compte et que pour s'en débarrasser il faut travailler suivant chacun des axes, enfin bref.

Bon si on veut résoudre cette équation différentielle (ce qui n'est pas demandé), on va écrire l'équation caractéristique:

     On remplace simplement par r², par r et x par 1.

On a une équation du 2nd degré, on a :



Donc les racines sont:    et          (Bon si tu préfères passer par le calcul du discriminant tu trouveras la même chose.)

Ces racines peuvent se mettre sous la forme: r=j

On a donc une solution complexe conjuguée, la solution sans second membre de cette équation différentielle est:



Ce qui nous donne dans notre exercice:

Voilà, tu as la solution générale de ton équation différentielle car le second membre est nul mais il faut déterminer les constantes A et B grâce aux conditions initiales qui sont précisées dans l'énoncé (qui ne le sont pas ici).


Sinon pour répondre à la question 4, ton équation différentielle est sous la forme:

En identifiant on trouve que:    donc  

On sait que    donc :  

On trouve bien:

Si tu ne comprends pas une étape, n'hésite pas à poser la question

Tout d'abord merci pour cette réponse rapide . Mais je n'ai pas tout compris.... Surtout à partir des racines, je ne comprends pas pourquoi il y a présence des j. Ensuite je n'ai pas compris comment tu fais pour passer de r=j   à ===>   x(t)=exp ....

Sinon pour la question 4, j'ai compris merci.

la résolution de l'équation différentielle n'est pas demandée car ce type de solution est du niveau de prépa  en term on voit juste:

y'=ky  solution=> Ce^kx   C

et

y'=ky+b solution=> Ce^kx + b/k

dites moi si je me trompe!

donc si j'ai raison (à vérifier) pas la peine de t'embêter avec la résolution sauf si tu veux faire de la physique (et des maths en locurence) plus poussée en post bac.

Alors pour la présence des j c'est assez simple. Je suppose que le cours sur les nombres complexes est vu en terminale (en tout cas il l'était quand j'étais au lycée). Un nombre au carré ne peut pas être négatif, c'est pour ça qu'on a inventé les nombres imaginaire avec j²=-1, ce qui te permet d'avoir des nombres au carré qui sont négatif. Par exemple: x=4j --> x²=16.j²=-16

Une autre façon de le voir c'est : x²=-16  -->

Si tu n'as pas vu ça laisses tout ça de côté et occupes toi seulement de la résolution d'équation différentielle du premier ordre.

Sinon, si tu regardes ton cours de maths, quand tu pars de l'équation caractéristique: a.r²+b.r+c=0, tu calcules les racines de ce polynôme avec le discriminant, si tu as deux racines réelles alors la solution à l'équa diff sans second membre est:

Si tu as une racine double, la solution est:

Et si tu as deux racines complexes conjuguées, la solution est:    avec .

Mais comme l'a dit Antoin_e, je ne pense pas que la résolution d'équation différentielle soit demandée en terminale donc tu peux faire l'impasse dessus (pour le moment).

en gros j(en physique)=i(en maths) i²=j²=-1