Inscription / Connexion Nouveau Sujet
Equation de trajectoire
Bonjour, voici l'exercice pour lequel j'aimerais avoir de l'aide :
Alex se trouve dans le téléphérique de Grenoble et fait tomber son téléphone alors qu'il se trouve au dessus de la rivière Isère . Son téléphone est garanti résistant à l'eau donc il se rassure pensant que son téléphone tombera dans l'eau et non sur le quai.
Pendant sa chute, le smartphone sera considéré comme un point matériel de masse m=235g et ne subissant aucune action de la part de l'air .
Au moment du lâcher pris comme origine des dates, la smartphone possède la même vitesse et le même angle de lancer que le téléphérique Vo = 5,65 m et α=28°
On choisit l'origine du repère Oxy au point correspondant à la position du téléphone au moment du lâcher . A ce moment précis, le téléphone se trouve à une hauteur h=75m de la surface de l'eau à une distance d=17m du quai.
Pour simplifier , on suppose que le quai se trouve à la même altitude que l'eau .
Le smartphone tombera il sur le quai ou dans l'eau ?
Voila , je veux savoir par où je devrais commencer pour répondre au problème comment il n'y a aucune autre question . Je pensais a trouver les équations horaires en premier puis l'équation de trajectoire mais je ne sais pas comment répondre ensuite au problème .
Merci d'avance
Bonjour,
L'énoncé ne précise pas si le téléphérique est en train de monter ou de descendre.
Les équations horaires du téléphérique sont suffisantes pour répondre à la question posée.
Soit C le point de chute du téléphone : Si x(C) < 17m la chute a lieu dans l'eau.
Bonjour,
Merci, j'ai donc pu posé :
x(C) = [ Vo² · sin(2α) + H ] / g
soit en remplaçant :
x(C) = [ (5,65)² · sin(2·28 ) + 75 ] / 9,81 = 10,34
Comme x(C) < 17 m , alors la chute a lieu dans l'eau .
Est-ce bien cela ? Je voulais savoir si j'ai bien placé le H dans mon équation s'il vous plait
Merci , bonne soirée
Bonjour,
L'énoncé ne précise pas si le téléphérique est en train de monter ou de descendre.
Les équations horaires du téléphérique sont suffisantes pour répondre à la question posée.
Soit C le point de chute du téléphone : Si x(C) < 17m la chute a lieu dans l'eau.
Bonjour,
Merci, j'ai donc pu posé :
x(C) = [ Vo² · sin(2α) + H ] / g
soit en remplaçant :
x(C) = [ (5,65)² · sin(2·28 ) + 75 ] / 9,81 = 10,34
Comme x(C) < 17 m , alors la chute a lieu dans l'eau .
Est-ce bien cela ? Je voulais savoir si j'ai bien placé le H dans mon équation s'il vous plait
Merci , bonne soirée
Le terme V0² est le carré d'une vitesse.
Le terme sin(2α ) est un nombre sans dimension
Donc V0² * sin(2α ) est aussi le carré d'une vitesse.
Le terme V0² * sin(2α ) + H est la somme du carré d'une vitesse avec une hauteur ce qui est rigoureusement impossible.
On en déduit que la relation ( non justifiée) x(C) = [ Vo² · sin(2α) + H ] / g est fausse.
Il te faut établir les équations horaires sans utiliser des "formules" pêchées on ne sait où et qui ne s'appliquent pas ici.
Le terme V0² est le carré d'une vitesse.
Le terme sin(2α ) est un nombre sans dimension
Donc V0² * sin(2α ) est aussi le carré d'une vitesse.
Le terme V0² * sin(2α ) + H est la somme du carré d'une vitesse avec une hauteur ce qui est rigoureusement impossible.
On en déduit que la relation ( non justifiée) x(C) = [ Vo² ·sin(2α) + H ] / g est fausse.
Il te faut établir les équations horaires sans utiliser des "formules" pêchées on ne sait où et qui ne s'appliquent pas ici.
D'accord, voici ce que j'avais fais au brouillon :
vecteur a { ax= 0 et ay = -g
vecteur V { vx= cte 1 =Vo · cos(α) et vy = -gt + cte 2 =-gt+Vo · sin(α)
On en déduit les équation horaires :
{ x= Vo · cos(α) · t + cte3 à t=0 cte 3 = 0
et y = -1/2 gt² + Vo · sin(α) · t + cte 4 à t=0 cte 4 = h
donc on en déduit l'équation de trajectoire :
on a t=x/ Vo · cos(α)
donc y= -g/2 · (x/ Vo · cos(α) )² +Vo · sin(α) · (x/ Vo · cos(α)) + h
donc :
y = -g/(2 · Vo² · cos²(α) ) · x² + tan (α) · x + h
Est-ce correct jusque là ? Je ne comprend pas aussi quand est ce que je dois utiliser la masse comme elle est donnée .
Merci
Oui, tu es sur la bonne voie mais attention aux contraintes imposées par l'énoncé.
On choisit l'origine du repère Oxy au point correspondant à la position du téléphone au moment du lâcher
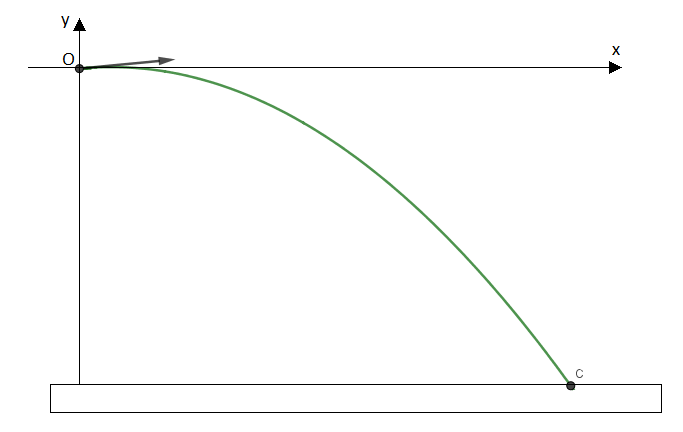
Ah oui j'ai mal noté les coordonnées j'ai oublié de préciser le O .
Et donc maintenant je peux en déduire x(C) ?
Oui, tu es sur la bonne voie mais attention aux contraintes imposées par l'énoncé.
On choisit l'origine du repère Oxy au point correspondant à la position du téléphone au moment du lâcher

Ah oui j'ai mal noté les coordonnées j'ai oublié de préciser le O .
Et donc maintenant je peux en déduire x(C) ?
Oui, quand tu auras obtenu l'équation correcte de la trajectoire il suffira de calculer l'abscisse du point C sachant que son ordonnée vaut -75m ( Voir mon schéma )
Remarque : La masse est une donnée superflue
Oui, quand tu auras obtenu l'équation correcte de la trajectoire il suffira de calculer l'abscisse du point C sachant que son ordonnée vaut -75m ( Voir mon schéma )
Remarque : La masse est une donnée superflue
Est - ce que l'équation de trajectoire est juste comme ça :
y = -g/(2 · Vo² · cos²(α) ) · x² + x · tan (α) + h
L'équation que tu donnes n'est pas fausse, mais elle ne répond pas à la contrainte de l'énoncé que j'ai déjà évoquée.
L'équation correcte est :
L'équation que tu donnes n'est pas fausse, mais elle ne répond pas à la contrainte de l'énoncé que j'ai déjà évoquée.
L'équation correcte est :
D'accord merci beaucoup , et pourquoi la hauteur h n'intervient- elle pas dans l'équation ?
L'équation de la trajectoire dépend du repère choisi.
C'est pour cette raison qu'il est impératif de définir ce repère dans le cas où l'énoncé ne le fait pas.
Dans le repère que tu as choisi sans le définir les coordonnées du téléphone au moment ou commence sa chute sont ( 0 ; h ) et celles de son point de chute sont ( xC ; 0 )
Dans le repère imposé par l'énoncé les coordonnées du téléphone au moment ou commence sa chute sont
( 0 ; 0 ) et celles de son point de chute sont ( xC ; -h )
Bien entendu, quel que soit le repère choisi on trouvera la même valeur pour l'abscisse xC du point de chute.
L'équation de la trajectoire dépend du repère choisi.
C'est pour cette raison qu'il est impératif de définir ce repère dans le cas où l'énoncé ne le fait pas.
Dans le repère que tu as choisi sans le définir les coordonnées du téléphone au moment ou commence sa chute sont ( 0 ; h ) et celles de son point de chute sont ( xC ; 0 )
Dans le repère imposé par l'énoncé les coordonnées du téléphone au moment ou commence sa chute sont
( 0 ; 0 ) et celles de son point de chute sont ( xC ; -h )
Bien entendu, quel que soit le repère choisi on trouvera la même valeur pour l'abscisse xC du point de chute.
Ah oui donc avec les coordonnées C(xc ; -h ) j'ai :
C { Cy = -75 et Cx = ?
on pose y=-75 soit
-75 = -g/(2 · Vo² · cos²(α) ) · xc² + tan (α) · xc
-75 = [-g/(2 · Vo² · cos²(α) ) · xc + tan (α) ] · xc
soit
xc = (2 · Vo² · cos²(α) · tan (α) + 75 ) / g
On trouve donc
xc = (2 · 5,65² · cos²(28) · tan (28) + 75 ) / 9,81 = 9,16
Donc le téléphone tombera dans l'eau
Est - ce que l'équation est juste ?
Merci
Est - ce que l'équation est juste ?
Non.
L'équation à résoudre est :
Il s'agit d'une équation du 2e degré dans laquelle la seule inconnue est xc
Est - ce que l'équation est juste ?
Non.
L'équation à résoudre est :
Il s'agit d'une équation du 2e degré dans laquelle la seule inconnue est xc
Ah d'accord merci, donc je fais :
Je cherche l'expression numérique de l'équation de trajectoire et je trouve :
yc= -0,35 xc² + 0,53xc
soit -75 = -0,35 xc² + 0,53xc
donc 0 = -0,35 xc² + 0,53xc + 75
Je cherche le discriminant Δ
Δ = 0,53² + 4 · 0,35 · 75 = 105
J'ai donc 2 solutions et je trouve
x1 = ( -0,53 - √105 ) / 2 · (- 0 , 35 ) = 15
x2 = ( -0,53 + √105 ) / 2 · (- 0 , 35 ) = - 14
On utilise x1 car elle est < à 17 donc le téléphone tombera dans l'eau
Voila, est-ce correct maintenant ?
Merci
Pardon ...
Remplacer dans mon dernier message :
" Mon équation de la trajectoire n'est pas la même que la tienne "
par
" Mon équation à résoudre n'est pas la même que la tienne . "
Pardon ...
Remplacer dans mon dernier message :
" Mon équation de la trajectoire n'est pas la même que la tienne "
par
" Mon équation à résoudre n'est pas la même que la tienne . "
Comment trouvez - vous : a= -0,197
car quand je pose -9,81/2 · 5,65² · cos 28² je trouve -0,3505 que j'ai arrondi à -0,35
et pour b j'ai arrondi au centième également
Merci
Pardon ...
Remplacer dans mon dernier message :
" Mon équation de la trajectoire n'est pas la même que la tienne "
par
" Mon équation à résoudre n'est pas la même que la tienne . "
Comment trouvez - vous : a= -0,197
car quand je pose -9,81/2 · 5,65² · cos 28² je trouve -0,3505 que j'ai arrondi à -0,35
et pour b j'ai arrondi au centième également
Merci
Voila ce que je pose sur ma calculatrice

L'écriture cos²(28) équivaut à (cos(28))² et pas à cos 28²
cos (28) = 0,883
cos(28²) = 0,438
cos²(28) = (cos(28))² = 0,779
L'écriture cos²(28) équivaut à (cos(28))² et pas à cos 28²
cos (28) = 0,883
cos(28²) = 0,438
cos²(28) = (cos(28))² = 0,779
D'accord merci , ça modifie donc mes calculs précédents :
yc= -0,197 xc² + 0,53xc
soit -75 = -0,197 xc² + 0,53xc
donc 0 = -0,197 xc² + 0,53xc + 75
Je cherche le discriminant Δ
Δ = 0,53² + 4 · 0,197 · 75 = 59
J'ai donc 2 solutions et je trouve
x1 = ( -0,53 - √59 ) / 2 · (-0,197 ) = 21
x2 = ( -0,53 + √59 ) / 2 · (-0,197 ) = - 18
On utilise x1 comme c'est la valeur positive qui nous intéresse, et comme 21 > 17, alors le téléphone tombe sur le quai .
Est - ce juste maintenant ?
Merci
Oui, c'est exact.
Attention tout de même de ne pas oublier les unités.
Comme 21m > 17m le téléphone tombe sur la quai.
De toutes façons même en cas de chute dans l'eau, Alex avait bien peu de chances de récupérer son téléphone au fond de l'Isère ! ! ! 
Oui, c'est exact.
Attention tout de même de ne pas oublier les unités.
Comme 21m > 17m le téléphone tombe sur la quai.
De toutes façons même en cas de chute dans l'eau, Alex avait bien peu de chances de récupérer son téléphone au fond de l'Isère ! ! !

Oui c'est vrai !
Merci beaucoup pour votre aide, je vous souhaite une bonne soirée !


