Niveau terminale

Equation de mouvement et sciences de l'Ingénieur.

Posté par
Kevin_01 06-03-14 à 15:35

Bonjour,

Ceci est un devoir de Sciences de l'Ingénieur sur les équation de mouvement.

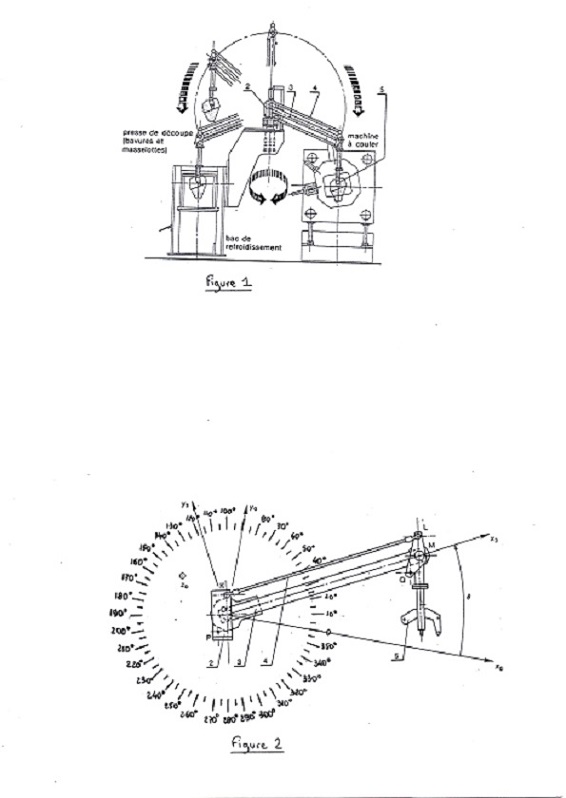
Le manipulateur de fonderie représenté sur la figure 1 permet de saisir la pièce lors de son éjection de la machine de coulée, d'assurer son transport vers le bac de refroidissement et vers la machine de dèmasselotage et d'ébavurage.

Soit $R0 (0,x0,y0,z0)$ le repère lié au bâti définissant la position initiale du manipulateur face à la machine à couler et $R3 (0,x3,y3,z3)$ le repère lié au bras repère 3.

On pose $\Theta =(x0,x3)$ et on donne $OM=1.7$ m.

Le mouvement de rotation du bras manipulateur comporte trois phase:

Phase 1: Mouvement de rotation uniformément accéléré pour $0 \le \Theta \le 15\degre$ , départ arrêté.
Phase 2: Mouvement uniforme pour $15 \degre \le \Theta \le 195 \degre$ à une vitesse angulaire de 1 rad/s.
Phase 3: Mouvement uniformément décéléré jusque l'arrêt pour $195 \degre \le \Theta \le 225 \degre$ .

Tout les encadrement sont écrit en degré et on doit les utilisé en  radian.

Questions:

1) Déterminer les équations de mouvement de la phase 1 ainsi que la durée de cette phase notée t1.

On sait que dans cette phase, le bras à une accélération donc $\ddot{\Theta}=cste$ .
On a donc pour t=0 :

$\begin{cases}  \ddot{\Theta}=cste\\ \\   \omega = \ddot{\Theta} t + \omega_0 \\ \\ \Theta= \frac{1}{2} \ddot{\Theta} t^2 + \omega_0 t + \Theta_0 \\ \end{cases}$

Condition initiale: Départ arrêté donc $\omega_0=0$ et je choisi $\Theta_0=0$ .

Donc :

$\begin{cases}  \ddot{\Theta}=cste\\ \\   \omega = \ddot{\Theta} t \\ \\ \Theta= \frac{1}{2} \ddot{\Theta} t^2 \\ \end{cases}$

A t=t1 , on sait que $\Theta=0.26$ rad soit 15 degrés et que $\omega =1$ rad/s.

Donc, on a:

$\begin{cases}  \ddot{\Theta}=0\\ \\   \omega =1 \\ \\ \Theta= \omega_0t + \Theta_0 = 1t = 0.26 \\ \end{cases}$

Aprés je suis perdu, car il me manque toujours 3 inconnu: l'accélération, la vitesse et le temps de la phase. Je suis bloqué.

Merci de m'aidez.

$Equation de mouvement et sciences de l\'Ingénieur.$

Posté par re : Equation de mouvement et sciences de l'Ingénieur. 06-03-14 à 18:28

Phase 1.

d²theta/dt² = K (constante)
w = K.t
theta = 1/2.K.t²

Or on sait que (en t = t1), la vitesse en fin de phase 1 est égale à la vitesse en début de phase 2 (il ne peut pas y avoir de discontinuité dans la vitesse).
---> w(t1) = 1 rad/s
et theta(t1) = 15/180 * Pi rad
theta(t1) = Pi/12 rad (angle parcouru pendant la phase 1)

1 = K.t1
15/180 * Pi = 1/2.K.t1²

15/180 * Pi = 1/2 * 1 * t1
t1 = 30.Pi/180 s
t1 = Pi/6 s (durée de la phase 1)

K = 1/t1
K = 6/Pi rad/s² (accélération angulaire pendant la phase 1)

Donc pour la phase 1:

Accélération angulaire : 6/Pi rad/s²
Durée de la phase 1 : Pi/6 s
w en fin de phase 1 : 1 rad/s
Angle parcouru durant la phase 1 : Pi/12 rad

Sauf distraction

Posté par re : Equation de mouvement et sciences de l'Ingénieur. 07-03-14 à 15:49

Pouvez-vous vérifié mes équations et le temps de chaque phase pour la phase 2 et la phase 3 ?

Phase 2:

$\begin{cases} \ddot{\Theta}=0\\ \\ \omega = 1 \\ \\ \Theta= t + 0.26 \\ \end{cases}$

Le temps de la phase 2 est de 3.14 secondes.

Phase 3:

$\begin{cases} \ddot{\Theta}= -0.94\\ \\ \omega = -0.94t + 1\\ \\ \Theta= \frac{1}{2} \times (-0.94)\times t^2 + t + 3.4 \\ \end{cases}$

Le temps de la phase 3 est de 1.06 secondes.

Est-ce correcte, merci.

Posté par re : Equation de mouvement et sciences de l'Ingénieur. 07-03-14 à 17:25

Phase 3

angle parcouru dans cette phase : 225-195 = 30° (Pi/6)

w(début de phase) = 1 rad/s
w(final) = 0 rad/s

durée de la phase : t3 = (Pi/6)/[(1-0)/2] = Pi/3 s
décélération : -1/(Pi/3) = - 3/Pi rad/s²

Sauf distraction.

Posté par re : Equation de mouvement et sciences de l'Ingénieur. 07-03-14 à 17:42

D'accord, merci

Je me suis pas tromper alors , car vous avez pris les valeurs exactes.
Je devais prend l'arrondie aux angle deux chiffres après la virgule.

Merci beaucoup pour la phase 1

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Equation de mouvement et sciences de l'Ingénieur.

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique