Inscription / Connexion Nouveau Sujet
energie potentielle d'un ressort
Bonjour
J'aimerais que vous m'indiquiez si je me suis trompee ou pas.
Un ressort de raideur k=14N.m-1 est etire de 7,5 cm par rapport a sa position de repos (position A). On detend le ressort afin qu'il se raccourcisse de 45 mm (position B)
a)Schematiser le ressort en precisant les deux positions A et B ainsi que la position de repos. J'ai juste une question pour cela, est que l'on detend le ressort en le raccourcissant de 45 mm par rapport a la position A ou par rapport a la position de repos?
b)Determiner l'energie potentielle elastique emmagasinee dans chaque cas.
Position de repos: EP= 0
Position A: Ep=14*(0,075)^2
c)Traduire la variation d'energie du ressort a l'aide d'un diagramme (c'est a dire?)
Bonjour,
a) Selon moi on le détend de la position A à la position B.
À la position B il est encore étiré
Si on le raccourcissait depuis la position de repos, il faudrait le comprimer. Ce n'est pas ce qu'indique l'énoncé.
b) Tu oublies un coefficient dans le calcul de l'énergie potentielle élastique du ressort pour la position A
c) Un graphique : énergie potentielle élastique en fonction de l'étirement.

Il me semble que l'energie potentielle elastique se calcule avec la formule: k*x^2 donc pour la position A cela correspond a ce que j'ai deja ecrit.
Je vais verifier mais pour l'instant je ne vois pas
merci a toi
Si l'axe des x est parallèle à l'axe du ressort, de vecteur unitaire  ,
,
l'origine O étant prise à l'extrémité libre du ressort quand celui-ci n'est ni étiré ni comprimé
le sens positif de l'axe correspondant à la direction dans laquelle on étire le ressort :
Quand le ressort est étiré d'une quantité x
la force de rappel qu'il exerce vaut
Pour accroître son étirement d'une quantité dx
il faut une force
qui fournira le travail
L'énergie potentielle élastique du ressort quand celui-ci est étiré de la quantité  l vaut donc
l vaut donc
intégrale que tu sais calculer...

merci beaucoup mais je ne comprends pas pourquoi il faut utiliser une integrale,il me semblait que c'etait plus simple, je verifierais.
"Je vérifierai..." : la confiance règne !
_________
Je t'ai dit (message du 19 mai à 11 h 18) que tu oublies un coefficient.
Tu as dit (message 20 mai à 11 h 03) que tu vérifierais
Je te fais la démonstration du calcul de l'énergie potentielle élastique (message du 20 mai à 11 h 52) afin que tu puisses vérifier que tu oublies un coefficient...
Alors, vérifie !

Excuse -moi donc si j'ai bien compris :
Epe= 0,5 *14*(0,075)^2 pour la position A
Pour la position B= Epe- 0,5*14 * (0,075-0,0045)^2
Pour la position A : Epe=0,5 *14*(0,075)^2 =0,04 J
Pour la position B: Epe=0,5*14 * (0,075-0,0045)^2=0,034J
Oui pour la position A
Non pour la position B
45 mm = 0,045 m (et non pas 0,004 5 m)
Pour B : Epe = 0,0063 J
Dernière question :
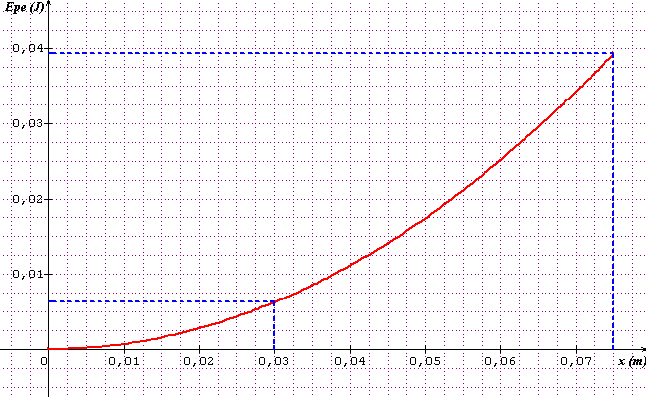
Je pense que c'est un graphique de ce genre qui répond à la question.



