Inscription / Connexion Nouveau Sujet
Energie cinétique
Bonjour, pourriez-vous m'aider svp ?
Je vous joins l'image
Un petit objet de masse m modélisé par un point est pendu au bout d'un fil inextensible de longueur L (voir figure)
1/ dresse le bilan des forces
2/ on lâche l'objet du point A. Exprime sa vitesse vb au point B en fonction de g, L et 
3/ Quelle est sa vitesse au point C?
4/ On lance maintenant l'objet du point A avec une vitesse va tangente au cercle vers la gauche. Exprimer la valeur minimale de la norme va pour que l'objet aille jusqu'au point D en fonction de g, L et . La calculer
** Fichier supprimé **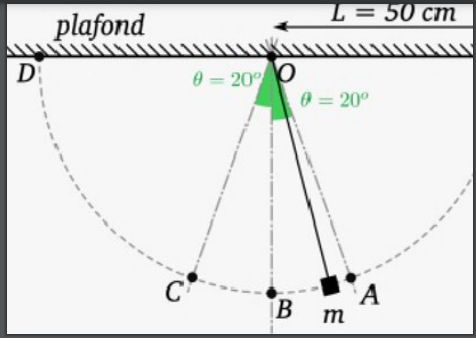 
malou edit
Voici mes réponses :
1/ Les forces de frottements (négligeables), son poids (P) et la tension du fil (T)
2/ Énergie cinétique en B : 1/2 mV²(B)
Énergie cinétique en A : 1/2 mV²(A)=0 car v(A) est nul
Travail de la tension T : nul car la direction de la force (la tension) est perpendiculaire à son axe d'application, (l'axe en O)
Travail du poids : mgx AB
et là je ne trouve pas AB??
Bonjour
Revois ton cours sur le travail des forces. Le travail du poids s'écrit de façon générale :
W=m.g.h
où h est la diminution d'altitude.
Refais une figure claire sur laquelle figurera h. Tu pourras alors facilement exprimer h en fonction de L et de .
Bonjour,
Tu écris :
Travail du poids : mg x AB
Ce n'est pas correct, le travail du poids dépend de la différence d'altitude entre les points A et B, et donc ...
Bonjour Candide
Avant de poster, tu peux cliquer, en bas de l'éditeur, sur la phrase écrite en rouge : "Vérifier la présence de nouvelles réponses".
Une réponse : "Pas de nouveaux messages" évite les "posts croisés". 
ok alors P=mxgx(za-zb)
mais cela ne me dit toujours pas à quoi correspond za??
Zb= OB donc egal à L mais Za???
Ce schéma ainsi que quelques connaissances en trigonométrie devraient t'aider pour trouver h=zA - zB
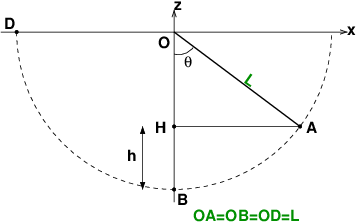
ah mais oui en utilisant le projeté orthogonal et les formules de trigo!! Ça me donne :
cos=OH/OA
donc OH= OA cos
ce qui me donne
P=mgx(OAcos-L)
= mg(Lcos-L)
=mgL(cos-1)
c'est ça?
Tu es sûr de ne pas confondre le poids P avec le travail du poids noté W ?
Attention aussi au signe de W. Lorsque l'altitude diminue, le travail du poids est positif.
Désolé, je me suis mal expliqué
Je réponds à la question 2/ en utilisant le théorème de l'Ec
1/2mV2B= mgx(Zb-Za)
1/2mV2B=mg(OB-OH)
1/2mV2B=mg(L-Lcos)
et oui merci je me suis bien trompé dans l'expression d'avant
Juste une erreur de signe à la première de tes trois formules. L'axe (O,z) est orienté vers le haut de sorte que z désigne l'altitude.
W=m.g.(zA - zB) = m.g.h >0
puis :
h=OB - OH comme tu l'as écrit, ce qui t'a conduit au résultat correct.
Merci
j'obtiens donc VB=7.69x10-1
et pour Merci
j'obtiens donc VB=7.69x10-1 à la question 3/ je fais 2pour la calculer
et j'obtiens VC=1.51
Pour 4/ je procède de même avec VD=0 et Va= - 
(2gx(L-Lcos))
Mais je pense que le signe - est bon car distance DA est negative donc cela devient positif?
VB=7.69x10-1
Attention : une application numérique sans unité, lorsque celle-ci existe, est en général considérée comme fausse.
Question 3 : C possède la même altitude que A ; donc ...
Pour 4 : l'adaptation de la formule précédente du poids conduit à :
WAD = m.g.(zA - zD)
Cette différence d'altitude est effectivement négative mais il faut revoir ta formule... Trouver vA <0 n'a pas de sens dans ce contexte.
oui désolé une autre erreur de ma part : m/s
Ok pour Vc=0m/s du coup
Mais alors je ne comprends pas votre formule WAD = m.g.(zA - zD) car 
EC est bien égale à l'etat final (D) - état initial (A) non ?
dans ce cas WAD=m.g.(zD-zA)?
on va trouver un EC = -1/2m.g.v2A
donc en déplaçant le signe - dans l'égalité de l'autre coté a obtient certainement ce changement ZA-ZD ..j'ai compris
Mais est-ce-bien égale à 110°?(90+20)?
bon j'ai procédé différemment et j'ai trouvé une VA=3.04m/s
J'ai tout simplement commencé par écrire 1/2 mV²(D) - 1/2 mV²(A) = -1/2 mV²(A).
Puis j'ai décomposé le travail des forces en calculant d'abord mon travail du poids de A en B = m.g.L(1-cos
Pui travail de Ben D = -mgL(1-cos90°) car on remonte
J'additionne ces deux forces et le signe - s'annule
du coup j'ai VA=(2gLcos)
OK pour 3. Pour 4, ton résultat est correct mais l'expression du travail du poids peut s'exprimer directement sans décomposer en deux étapes.
WAD = m.g.(zA - zD)
Reprend mon schéma du 16-01-24 à 19:16 ; tu obtiens simplement comme différence d'altitude :
(zA - zD)=-OH
où OH est la distance (donc valeur positive) de O à H, valeur positive qui s'exprime simplement en fonction de L et . Tu as déjà eu l'occasion d'exprimer cette distance...
Annuler
connectez vous