Inscription / Connexion Nouveau Sujet
[Electricité] Résolution équation différentielle second ordre
Bonjour 
En électricité on étudie l'équation différentielle du second ordre suivante :
avec
,
,
et
des constantes.
Sauf qu'on se place dans les conditions idéales c'est à dire qu'on impose .
Si on ne fait pas cette hypothèse comment doit-on s'y prendre pour résoudre cette équation ?
Merci

Appelons R+r = R' pour faciliter l'écriture.
p²L + R'p + 1/c = 0
p²LC + R'C.p + 1 = 0
p = (-R'C +/- V(R'²C²-4LC))/(2LC)
1°) si (R'²C²-4LC) < 0
p = -(R'/(2L)) +/- i.(V(4LC - R'²C²))/(2LC)
q = e^(-(R'/(2L))t) * [A(sin(((V(4LC - R'²C²))/(2LC)).t) + B.cos(((V(4LC - R'²C²))/(2LC)).t)]
A et B étant des constantes réelles dépendant des conditions initiales.
-----
2°)
Si (R'²C²-4LC) > 0
q = A.e^(((-R'C + V(R'²C²-4LC))/(2LC)).t) + B.A.e^(((-R'C - V(R'²C²-4LC))/(2LC)).t)
A et B étant des constantes réelles dépendant des conditions initiales.
-----
3°)
Si (R'²C²-4LC) = 0
q = A.e^(-(R'/(2L))t) + B.t.e^(-(R'/(2L))t)
A et B étant des constantes réelles dépendant des conditions initiales.
-----
Sauf distraction. 
bonjour
la résolution de ce type d'équation différentielle n'est plus au programme de terminale!!
néanmoins voici la méthode:
soit une équation différentielle de 2ème ordre du type y''+ay'+by=o qui a pour équation caractéristique r²+ar+b=0 de discriminant 
* si  >0: f(x)=
>0: f(x)= 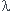 e(r1.x)+
e(r1.x)+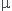 e(r2.x) ou r1 et r2 sont les racines de l'équation caractéristique
e(r2.x) ou r1 et r2 sont les racines de l'équation caractéristique
* si  =0: f(x)=(
=0: f(x)=(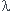 x+
x+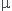 )e(r.x) où r est la racine double de l'équation caractéristique
)e(r.x) où r est la racine double de l'équation caractéristique
* si  <0: f(x)= (
<0: f(x)= (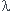 cos
cos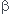 x+
x+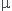 sin
sin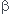 x)e(
x)e(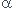 x) où r1=
x) où r1=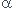 +i
+i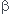 et r2=
et r2=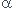 -i
-i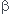
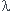 et
et 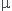 sont des constantes à déterminer a l'aide des conditions de l'exercice
sont des constantes à déterminer a l'aide des conditions de l'exercice
J'espère avoir répondu à ta question
Bonsoir J-P 
On introduit mais que représente-t-il ? Je ne vois pas d'où il vient.
Merci encore une fois de te soucier de mes problèmes 
Ok donc le viendrait de l'équation caractéristique d'après alexc, mais je relance ma question : elle sort d'où ?

alexc a appelé "r" ce que j'ai appelé "p"
Peut-être une modification des conventions ?
Pour moi, et dans de nombreux ouvrages on note p, mais c'est sans importance.

L'équation caractéristique c'est ce qu'on utilise pour résoudre les équadiffs d'ordre 2 (ou plus) quand il n'y a pas de second membre et que les coefficients sont constants( ce qui est le cas ici)
Voici la méthode générale :
On considère l'équation différentielle du second ordre suivante :
Soit (e) l'équation caractéristique de (E):
Démontrons la propriété suivante.
Soit f une fonction définie sur , mais à valeur dans
, de la forme
, avec
.
En effet, on a :
car
On admettra celle qui suit (en fait, c'est démontrable à notre niveau, mais c'est vachement long, et très très technique, donc j'admets, mais si tu veux ...):
Soit et
deux solutions distinctes et linéairement indépendantes de (E) sur un intervalle (non réduit à un point) I. Alors, les solutions de (E) sur I sont l'ensemble des fonctions de la forme
avec .
Une fois qu'on a fait cela, on peut s'attaquer au reste.
1) (e) admet deux solutions réelles distinctes et
.
D'après la propriété du dessus, on connaît deux solutions de (E).
Ce sont les fonctions et
, avec
et
D'après la propriété admise, l'ensemble des fonctions {f} solutions de (E) sur sont les fonctions de la forme:
.
Les constantes A et B étant déterminées grâce aux conditions initiales (tout comme pour les équadiffs du premier ordre)
2) (e) admet une solution double .
Dans ce cas, on connaît une solution de (E). C'est la fonction définie sur I par
C'est déjà bien, sauf que c'est insuffisant pour conclure.
Dans ce cas, deux solutions : soit on fait comme pour les equadiffs du premier ordre, càd qu'on prend une fonction quelconque solution de (E), et puis on déballe tout.
Soit, on prend la méthode courte.
En effet, on remarque ( ) que la fonction
) que la fonction est solution aussi de (E).
On a donc bien nos deux solutions et
On peut donc conclure que l'ensemble des fonctions {f} solutions de (E) sur I, est l'ensemble des fonctions de la forme :
3) (e) admet deux solutions complexes conjuguées et
Là c'est marrant. 
D'après la première propriété, on connaît deux fonctions solutions de (E) sur I.
Ce sont les fonctions définies par et
Ouaip, mais on va pas loin avec ca. Ce sont des fonctions à variables complexes, donc pour l'étude ... bof bof.
Posons et
avec
Par conséquent:
et
Ou encore:
et
Continuons :
Posons et
Toujours pas le flash ?(regarde au dessous si non)
et
et
sont bien deux solution linéairement indépendantes sur
. De plus, ce sont aussi des solutions de (E). On a donc bien nos deux solutions.
On peut donc conclure, en disant que l'ensemble des fonctions {f} solutions de (E) sur I sont toutes les fonctions de la forme :
Traitons un exemple.
Pour le premier cas, et le deuxième, je te laisse faire.
Le troisième est plus intéressant.
Soit l'équation différentielle (E) suivante:
l'équation caractéristique associée à (E) est :
Résolvons (e).
(e) admet donc deux solutions complexes et
et
et
.
Par conséquent, l'ensemble des solutions {f} de (E) sur , sont l'ensemble des fonctions de la forme:
A vérifier.

Ayoub.
On admettra celle qui suit (en fait, c'est démontrable à notre niveau, mais c'est vachement long, et très très technique, donc j'admets, mais si tu veux ...):
Je veux

Dans ton exemple, je ne vois pas pourquoi
Même chose pour a
Skops

Skops >>
"a" et "b" ne représente pas les coeff de "x²+x+1" mais les parties réelles et imaginaires des racines.

Skops >>
Demain, je vais essayer de la poster ta démo. Mais je me suis trompé, c'est pas vraiment du niveau Terminale (c'est pour ça que je l'ai pas posté  )
)

Ayoub.
RAPPEL
Soient et
deux fonctions définies sur le même intervalle
.
On dit que deux fonctions et
sont deux fonctions sont proportionnelles s'il existe un
de
tel que pour tout x de I:
Soient et
deux solutions de l'équadiff
. Et soient
et
deux nombres réels.
On peut montrer facilement que est aussi une solution.
Donc, on peut conclure que toute combinaison linéaire de deux solutions de (E) est solution de (E).
Soient et
deux solutions non proportionnelles de (E). Et soit y une solution de l'équadiff.
On montre que y est une combinaison linéaire des deux solutions et
. C'est-à-dire, il existe
et
tel que:
On a:
et:
Pour déterminer: et
, il suffit de résoudre ce système:
Le déterminant de ce système est:
On admet que D(x) est non nul donc le système a une seule solution: .
Résultat: Toute solution de (E) est une combinaison linéaire de deux solutions non proportionnelles de (E).
** On va résoudre l'équadiff (E)
On cherche des solutions du genre: r est un réel.
y est solution de (E) équivaut:
et puisque la fonction exponnentielle ne s'annule jamais
donc:
Donc si r est solution de: donc:
est solution de (E)

Juste une petite remarque, j'ai fait une erreur de traduction
on dit pas fonctions proportionnelles mais fonctions associées 





