Inscription / Connexion Nouveau Sujet
Electricité, Puissance max (en W)
(re)Bonjour voici mon énoncé :
Un générateur de tension continue a une force électromotrice de 6V et une résistance interne de 2 ohm. De combien est la puissance maximale qu'il peut débiter dans un circuit résistif ?
Je sais que P(élec) = E.I - r.I²
P(élec) est inconnu tout comme l'intensité I.
Comment peut-on faire pour calculer I max dans un premier temps ?
Ps : la réponse est P(max)= 4,5 W mais le résultat m'importe peu, seule la méthode compte.
Merci
Re - bonjour,
Soit R la valeur du circuit résistif.
Suppose R très faible, beaucoup plus faible que la résistance interne r : l'intensité I du courant sera forte. Mais l'essentiel de la puissance sera délivrée dans le générateur et pas dans le circuit résistif...
Suppose R très élevée, beaucoup plus élevée que la résistance interne r du générateur : l'intensité I du courant sera faible. Il y aura peu de puissance délivrée dans le circuit résistif...
Tu te trouves devant un problème connu : la puissance délivrée dans le circuit résistif est une fonction de la résistance R de ce circuit et tu cherches un maximum...
À toi !

Soit R la résistance connectée sur le générateur.
E - rI - RI = 0 (loi des mailles)
I = E/(r+R)
La puissance débitée dans R est : P = RI²
P = E².R/(r+R)²
Il faut donc chercher la valeur de R (en fonction de r) qui rend P maximum ... et puis en déduire Pma
Sauf distraction. 
Salut JP je dois avouer que je sèche malheureusement ...
Peux tu me montrer le détail du calcul que je puisse comprendre avec les valeurs concrètes ?
E - rI - RI = 0 (loi des mailles)
I = E/(r+R)
La puissance débitée dans R est : P = RI²
P = E².R/(r+R)²
Cela se réduit ensuite à une simple étude des variations d'une fonction...
P = E².R/(r+R)²
On dérive par rapport à R :
P'(R) = E².((r+R)²-2R(r+R))/(r+R)^4 = E².(r+R-2R)/(r+R)³ = E².(r-R)/(r+R)³
On a donc :
P'(R) > 0 pour R dans [0 ; r[ --> P(R) est croissante.
P'(R) = 0 pour R = r
P'(R) < 0 pour R dans ]r ; +oo[ --> P(R) est décroissante.
Et donc P(R) est maximum pour R = r = 2 ohms et ce max est Pmax = P(r) = E².r/(r+r)² = E²/(4r) = 6²/(4*2) = 4,5 W
-----
Sauf distraction. 
" P = E².R/(r+R)²
P'(R) = E².((r+R)²-2R(r+R))/(r+R)^4 = E².(r+R-2R)/(r+R)³ = E².(r-R)/(r+R)³ "
donc P est la primitive de P' ...
Je crois que je vais aller sur ile de math car j'ai des lacunes sur les dérivés et primitives...
Mais dans l'esprit... le fait de faire ici la dérivée permet de trouver des valeurs limites c'est bien cela? ou cela sert'il à simplifier une équation?
Je n'ai pas encore vu cela...
Je n'ai pas encore vu cela...
Tu n'as pas appris à étudier les variations d'une fonction ?

Non... Je suis autodidacte on vas dire mais avec votre aide les choses sont plus abordables...
Je viens de voir plusieurs vidéo sur internet montrant les différentes fonctions et leur dérivées... A apprendre par cœur en soit...
Mais a quoi sert véritablement de faire la dérivée d'une équation? De trouver différentes valeurs possible d'un "x" c'est cela?
Etre autodidacte est bien.
Il faut cependant respecter une certaine hiérarchie dans ce qu'on tente d'apprendre.
Ici, il faut pouvoir rechercher un maximum d'une fonction.
Pour le faire, il est préférable (même si on peut toujours tourner autour) d'avoir les bases mathématiques utiles à la résolution du problème.
Dans le cas présent, cela passe par savoir étudier les variations d'une fonction, études pour lesquelles la notion de dérivées est "presque" obligatoire.
Il faut donc, à mon sens, que tu commences par approfondir quelques bases mathématiques, avant de t'attaquer à des problèmes comme celui posé.
On peut évidemment "tourner" autour de la difficulté en partant de l'expression : P = E².R/(r+R)² et en passant directement en numérique avec E = 6V et r = 2 ohms, on trouve alors :
P = 36.R/(2+R)²
On calcule ensuite les valeurs numériques de P pour différentes valeurs de R ... et on cherche la valeur de R pour laquelle le résultat sera max.
----

Salut JP oui j'ai essayé de faire comme la seconde méthode que tu ma suggéré. C'est plus simple mais plus approximatif, de plus j'aimerai vraiment savoir utiliser et comprendre les dérivées.
Peux on essayer ici de faire le raisonnement avec les dérivées (dans le cas concret de notre exercice) ou c'est plus approprié sur ile des math?
Si oui voici le debut de mon raisonnement:
J'ai une équation : P= 36R/(R+2)²
Je souhaite connaitre les différentes valeurs de R
Je calcul donc la dérivée sur la base de (U/V)'= ((U'.V)-(U,V'))/V²
Ici : U= 36R U'=36
V=(R+2)² V'=2(R+2)
Donc P'R= (((36x(R+2)²)-(36Rx2(R+2)))/(R+2)^4
P'R= (((36x(R+2)-(36Rx2)))(R+2)^3
P'R= (36R+72-72R)/ (R+2)^3
P'R= (-36R+72)/ (R+2)^3
(Coupez moi si je me trompe ^^)
Dans un premier temps cela est il juste ?
Si oui je vais ensuite essayer de trouver les différentes valeurs de R grâce au tableau de variation.
Jusque là, c'est bon.
Le tableau de variations doit (entre autre) permettre de trouver la (ou les) valeur(s) de R qui rendent la fonction P(R) maximale ...
Quelques exercices sur ce type de problèmes (études de fonctions), ici : (Lien cassé)

voici le tableau de variation, on peut remarquer que la valeur maximale de R est 2 ohm et la valeur minimale de R est -2 ohm
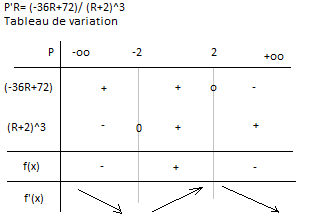
Ps j'ai oubli de mettre un double trait dans la dernière colone en dessous -2 car c'est une valeur interdite.
Merci JP pour les exercices je vais pouvoir travailler dessus
Bon, cependant, il est inutile d'étudier les variations pour R < 0, puisqu'une résistance est toujours >= 0.
Donc, il faut, ici, limiter l'étude de f(R) (et pas f(x comme écrit) pour R >= 0 (attention, la variable est ici R et pas P comme le suggère ton tableau)
De plus, tu as croisé f(x) et f'(x) dans le tableau.
Le tableau corrigé devrait être :

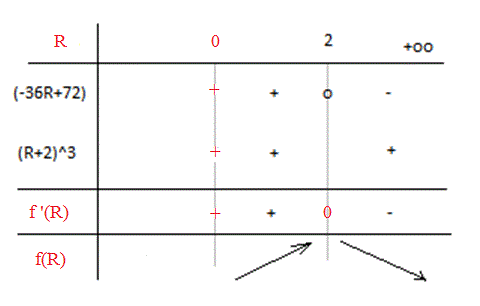
 merci JP
merci JP
