Inscription / Connexion Nouveau Sujet
Electricité, graphique
Bonjour, cet exercice me pose problème à un certain moment, je vais tout reprendre du début en vous expliquant ma démarche :
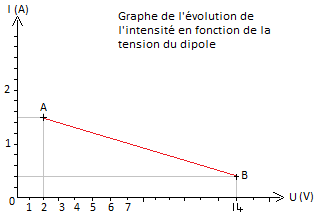
La caractéristique intensité-tension d'un dipôle linéaire passe par les deux point de fonctionnement A(300 mA ; 14 V) et B (1,5A ; 2,0 V).
(Répondre par vrai ou faux aux questions suivantes en justifiant) :
1) ce dipôle est à classer dans la catégorie des récepteurs
2) la loi de fonctionnement de ce dipôle peut se mettre sous la forme I = a.U+b avec a < 0 et b > 0
3) Lorsqu'il fonctionne au maximum de sa puissance, ce dipôle délivre une intensité de 850 mA
4) Si U = 10V, alors I = 1A
5) ce dipôle dissipe par effet Joule une puissance de type r.I².t
Dans un premier temps je cherche à représenter graphiquement ces données pour permettre de bien visualiser les choses.
J'ai donc deux points A et B avec les coordonnées.
Ma question : dois-je représenter I en fonction de U ou l'inverse ? Cela a-t-il une réelle importance de savoir quelle donnée sera sur l'axe des x et la quelle sur l'axe des y ?
Comme le dipole est linéaire, la loi liant U et I est de la forme : I = a.U + b
Des 2 points de fonctionnement donnés on tire :
0,3 = 14a + b
1,5 = 2a + b
système qui résolu donne : a = -0,1 et b = 1,7 ---> réponse à la question 2 : VRAI
----
3)
I = 1,7 - 0,1.U
U = 17 - 10I
P = UI
P = (17 - 10I).I
P = 17I - 10I²
P'(I) = 17 - 20I
P'(I) > 0 pour I < 0,85 A
P'(I) = 0 pour I = 0,85 A
P'(I) < 0 pour I > 0,85 A
La puissance P est donc max pour I = 0,85 A (850 mA) ---> réponse à la question 3 : VRAI
-----
4)
I = 1,7 - 0,1.U
Si U = 10 ---> I = 1,7 - 1 = 0,7 A ---> réponse à la question 4 : FAUX
-----
5)
P = 17I - 10I²
et donc énergie dissipée pendant une durée t : E = (17I - 10I²).t ... et donc différente de r.I².t
---> réponse à la question 5 : FAUX
-----
Sauf distraction. 
Question 1)
Ce dipôle n'est pas un récepteur (dipôle passif) car sa caractéristique ne passe pas par l'origine (d'après de lointains souvenir)
merci pour les autre réponses je bosse ça.
La question 5) était fausse a tous les coups oui car U.I.t est caractéristique de la formule de l'énergie (en j) alors que la formule de la puissance est du type: P= U.I ou P= r.I²
Merci jp et bonne après midi avec ce soleil!
A(300 mA ; 14 V) et B (1,5A ; 2,0 V)
Lorsque l'on veut calculer notre coefficient directeur a , nous utilisons la formule suivante: a=(yb-ya)/(xb-xa). Cela est correcte?
Prenons B(1,5A ; 2V) ... Xb=1,5 et yb=2 je me trompe?
Pourtant vous semblez avoir fait l'inverse...
J'ai fais (2-14)/(1,5-0,3)= -12/1,2 = -10
Vous trouvez l'inverse = -0,1
Tu as fait des erreurs que j'explique ainsi :
Avec A(300 mA ; 14 V) et B (1,5A ; 2,0 V), on suppose, en général que la première coordonnée est l'abscisse et le seconde l'ordonnée.
Donc, cette présentation de A et B spousse à penser que le courant est en abscisse et la tension en ordonnée.
MAIS, l'écriture I = a.U+b pousse à penser que le courant est en ordonnées et la tension en abscisses.
Et c'est à partir de là que tu t'es planté.
Pour remettre les "choses" dans un ordre moins piegeant, on aurait pu écrire :
I = a.U+b
avec A(14V ; 300 mA) et B(2,0V ; 1,5 A)
Cela ne change rien ... mais il y a moins de risque avec cette écriture de se tromper.
On a alors : a = (yb-ya)/(xb-xa) = (0,3 - 1,5)/(14-2) = -1,2/12 = -0,1
...
*****
Une autre manière pour voir qui avait raison.
J'ai trouvé : I = aU + b = -0,1 U + 1,7
Soit I = -0,1 U + 1,7
Et en remplaçant U et I par leurs valeurs données pour A (ou pour B) ... on trouve bien une identité.
En effet :
I = -0,1 U + 1,7 (1)
Pour A, on a : I = 0,3A et U = 14V qui satisfont bien la relation (1)
Pour B, on a : I = 1,5A et U = 2V qui satisfont bien la relation (1) également.
... conclusion, ma relation I = -0,1 U + 1,7 (qui correspond à a = -0,1 et b = 1,7) est bien correcte.

Ou alors plus simple si I=a.U+b. On peut dire aussi que y=ax+b si on remplace on voit bien que y=I et x=u
Donc on sait qui va en absisse et qui vas en ordonnée
On peut exprimer I en fonction de U : I = -0,1 U + 1,7
Mais on peut aussi exprimer U en fonction de I : U = -10 I + 17
-----
Dans le cas présent, on demandait les valeurs de a et b tels qu'on ait : I = a.U+b
Et dans ces conditions, on trouve a = -0,1 et b = 1,7 (on n'a pas le choix)
-----
Le plus facile n'est pas de passer par a = (ya-yb)/(xa-xb) et b = ...
Où il faut prendre garde à l'ordre dans le quel on a les coordonnées de A et B ...
Il suffit de partir (comme c'est demandé) de I = a.U+b et de remplacer U et I par les valeurs tirées des données A(300 mA ; 14 V) et B(1,5A ; 2,0 V).
Ainsi on ne peut pas se planter.
I = a.U+b avec A(300 mA ; 14 V) ----> 0,3 = 14a + b
et
I = a.U+b avec B(1,5A ; 2,0 V) ----> 1,5 = 2a + b
Il reste alors à résoudre le système trouvé, soit :
0,3 = 14a + b
1,5 = 2a + b
Ce qui donne facilement : a = -0,1 et b = 1,7
-----