Inscription / Connexion Nouveau Sujet
Dynamique des mouvements circulaires
Bonjour,
Je me permets de poster car je rencontre une difficulté avec un exercice, dont voici l'énoncé :
Pour une voiture, il est possible d'incliner la route d'un virage de rayon R, de manière à ce que la voiture puisse prendre le virage, même sans friction. Donner l'expression de l'angle  de la pente pour que la voiture puisse prendre le virage à une vitesse v sans tenir compte de la friction.
de la pente pour que la voiture puisse prendre le virage à une vitesse v sans tenir compte de la friction.
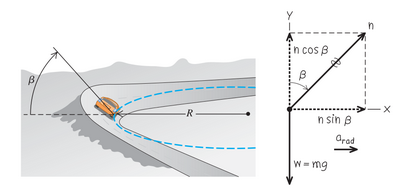
Je vous joins le diagramme des forces proposé par la correction de l'exercice.
En suivant le diagramme des forces, il faut que
 Fx = arad m = (v²/R)m
Fx = arad m = (v²/R)m
(où arad est l'accélération centripète, je la note ainsi pour rester cohérent avec le diagramme de forces)
Or,  Fx = n sin
Fx = n sin 
(où n est la force normale)
Donc, n sin  = (v²/R)m
= (v²/R)m
Or, il me semble que n devrait être égal à mg.cos , ce qui me donne une réponse fausse.
, ce qui me donne une réponse fausse.
Voilà donc ma difficulté : je n'arrive pas à comprendre pourquoi la force normale n'est pas bêtement l'inverse de la composante du poids perpendiculaire à la surface du virage...
Auriez-vous l'amabilité de m'aider ?
Cordialement,
Si désigne l'action de la route sur le mobile assimilé à un point matériel de masse m :
Le vecteur accélération est horizontal, dirigé vers le centre de la trajectoire, suivant "x" sur la figure.
Pour éviter tout risque de dérapage, le vecteur est perpendiculaire à la route, donc incliné de l'angle
 par rapport à la verticale ; cela apparaît bien sur la figure.
par rapport à la verticale ; cela apparaît bien sur la figure.
Projète la relation vectorielle précédente sur les deux axes. Une division "membre à membre" va te conduire à l'expression de tan( ).
).
(À nouveau désolé pour le double post)
À la réflexion, il y a quelque chose que je comprends pas.
Je comprends ce qui se passe mathématiquement. La somme des mouvements sur l'axe y est nulle, et la somme des mouvements sur l'axe x est la projection de N sur x. Ce qui nous donne deux équations qui nous permettent d'arriver à l'expression tan 
Mais alors, cela signifie que N est plus grand que W. Et c'est ça que je ne comprends, puisque, selon la définition physique de la force normale, il me semble que N devrait être égal à la composante de W perpendiculaire à la route.
Est-ce qu'il faut supposer (sans le faire intervenir dans les calculs) qu'il y a une force supplémentaire au poids qui n'est pas sur le diagramme de force, et qui fait que la pression totale exercée par la voiture sur la route est plus grande que celle due au seul poids ?
Pour que soit satisfaite la relation :
La réaction de la route doit avoir deux composantes :
1° : une composante verticale qui compense le poids comme tu l'as écrit ;
2° : une composante horizontale dans la mesure où le vecteur est un vecteur horizontal centripète.
La réaction du sol est ainsi de norme supérieure à la norme du vecteur poids.
D'accord, merci. Mais alors j'ai deux questions :
1) Pour être sûr que je comprenne bien ce qu'est la force normale : suivant la 3e loi de Newton, la force normale est une force de réaction, égale et opposée à la force exercée par un objet sur une surface. La force normale est toujours perpendiculaire à la surface. Donc, dans le cas d'un corps exerçant une force sur une surface en pente, est-ce que la force normale ne devrait pas toujours être équivalente à la projection sur la droite perpendiculaire à la surface en pente de la force totale exercée par le corps sur la surface en pente ?
2) Dans notre cas, si on considère que la composante en y de la force normale est la réaction au poids, alors, concernant la composante en x, à quelle force réagit-elle ?
Le mot "réaction" qui apparaît parfois dans l'énoncé de la troisième loi de Newton induit hélas souvent des incompréhensions. On préfère maintenant éviter d'employer ce mot et parler de principe des actions réciproques : si un corps A exerce une action sur un corps B de vecteur , le corps B exerce au même instant sur le corps A une action de vecteur :
Dans ces conditions, la prise en compte de toutes les forces conduit toujours et à chaque instant à une résultante de vecteur nul. C'est bien pour cela que la deuxième loi de Newton donnant l'accélération dans un repère galiléen ne prend en compte que les actions extérieures, c'est à dire les actions exercées sur le système étudié par le milieu extérieur.
Cela conduit à l'étude précédente qui a fourni la relation . Cette relation montre que l'action de la route sur le véhicule (j'évite d'utiliser le mot réaction, source de confusion comme déjà écrit) n'est l'opposé du poids que si le vecteur accélération est le vecteur nul.
D'accord, merci.
D'accord, merci. Mais alors j'ai deux questions :
Mais ce que je ne comprends pas, c'est que, sur le diagramme des forces, c'est la force normale qui fournit la force nécessaire pour donner l'accélération centripète. Mais, il me semble qu'ici, si on imagine que la voiture est un objet statique simplement posé sur la pente, la force normale devrait être égale à mg cos , i.e. à la projection du vecteur poids sur une droite perpendiculaire à la surface en pente. Ce que je ne comprends pas, c'est pourquoi la force normale n'est pas simplement égale à mg cos
, i.e. à la projection du vecteur poids sur une droite perpendiculaire à la surface en pente. Ce que je ne comprends pas, c'est pourquoi la force normale n'est pas simplement égale à mg cos . L'explication physique la plus raisonnable me semble être de considérer qu'il y a une force autre que le poids qui est exercée par la voiture sur la pente, due au fait que la voiture est en mouvement.
. L'explication physique la plus raisonnable me semble être de considérer qu'il y a une force autre que le poids qui est exercée par la voiture sur la pente, due au fait que la voiture est en mouvement.
(Navré, il y a eu interpolation d'une phrase, il faut lire le message sans "D'accord, merci. Mais alors j'ai deux questions")
Imagine l'automobile immobile sur la route inclinée. L'action de la route sur la voiture serait l'opposé du poids donc une force verticale orientée vers le haut. Une telle force ne serait pas normale à la route ; une telle force ne serait possible qu'en présence de frottement.
Ah, mais la force normale N qu'exerce la route sur la voiture, elle s'explique par la 3e loi de Newton, comme l'action réciproque de l'action que la voiture exerce sur la route, ou ai-je tout faux ?
Je ne comprend pas alors pourquoi la force normale (qui est, si je ne me trompe pas, la force réciproque exercée par une surface sur un corps exerçant une force sur cette surface) est définie comme toujours perpendiculaire à cette surface.
D'accord avec ton premier paragraphe mais je ne vois pas le rapport avec la suite... Puisqu'on s'intéresse ici à l'équilibre ou au mouvement du véhicule, autant se concentrer sur les forces exercées sur le véhicule par le milieu extérieur. Dans le cas le plus général, l'action de la route sur le véhicule peut se décrire comme une somme de deux vecteurs : un vecteur normal à la route noté souvent et un vecteur tangent à la route, souvent noté
. Ce dernier vecteur est le vecteur nul en absence de frottement , cas d'une route totalement verglacée par exemple. Ainsi, une voiture peut rester immobile sur une route en pente en présence de frottement ; elle se met à glisser dans le sens de la pente en absence de frottement si elle est initialement immobile.
Mais est-ce que la force normale n'est pas l'intégralité de la force réciproque exercée par la route sur la voiture ? Si la force réciproque au poids d'un objet exercée par une surface inclinée sur cet objet était "orientée vers le haut" (perpendiculaire au sol et de biais par rapport à la surface inclinée) et égale et opposée au poids, alors l'objet ne glisserait pas le long de la pente il me semble, non ?
Un conseil si je peux me permettre : si tu veux t'intéresser aux différents mouvements ou équilibres possibles du véhicule, concentre-toi exclusivement sur les actions extérieures. Le principe des actions réciproques est utiles dans un certain nombre de situations mais pas vraiment ici. Inutile de trop se disperser... Tu as donc à prendre en compte le poids du véhicule et l'action de la route sur celui-ci. Évite d'utiliser le mot "réaction" qui risque de t'induire en erreur.


 Physique en terminale
Physique en terminale