Inscription / Connexion Nouveau Sujet
Dynamique de rotation 5
Bonjour tout le monde, veuillez m'assister svp
Problème
Un solide (S) homogène est formé de 3 cylindres (C1), (C2) et (C3) accolés ayant même axe de révolution.
Les cylindres (C1) et (C3) sont identiques ; ils ont la même masse m et de même rayon r. Le cylindre (C2) a une masse M quatre fois plus grande (M = 4m) et un rayon R Deux fois plus grand (R = 2r).
Le solide (S) est mobile sans frottement autour d'un axe (
) confondu avec son axe de révolution.
La barre (B) homogène de masse M' = 3m est suspendue par 2 fils verticaux inextensibles et de masse négligeable, enroulés sur les cylindres (C1) et (C3) auxquels ils sont fixés par leurs extrémités. La barre (B) est abandonnée sans vitesse initiale.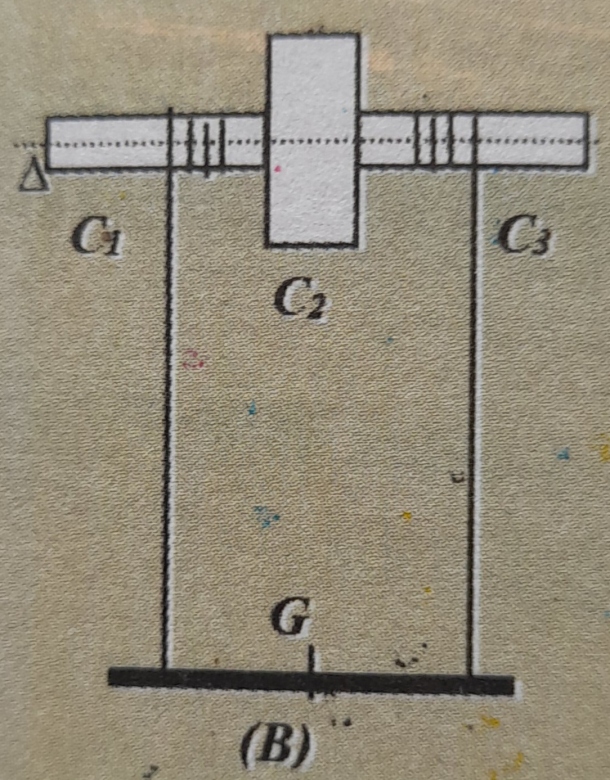 
1) Calculer en fonction de m et de r, le moment d'inertie du solide (S) par rapport à l'axe ().
2) Exprimer en fonction de m et de v (vitesse du centre d'inertie G de la barre) l'énergie cinétique du système (S) et (B).
3) En appliquant le théorème de l'énergie cinétique, que l'on énoncer, donner l'expression de v en fonction de g (intensité de pesanteur) et de h (hauteur de chute de la barre).
En déduire, en fonction de g, l'accélération a de la barre.
D'accord !
1) Expression du moment d'inertie du solide (S)
On pose J = J1 + J2 + J3
Mais J1 = J3 = ½mr² et J2 = ½MR² = 8mr²
Le moment d'inertie du solide (S) :
2) Expression de l'énergie cinétique du système (S) et (B)
L'énergie cinétique totale du système (S) + (B) est :
Ec = Ec(S) + Ec(B)
• Ec(S) = ½J.
²
• Ec(B) = ½M'v² = (3/2)m.v²
Mais J = 9mr² et = v/r
En remplaçant dans l'expression de l'énergie cinétique, je trouve ceci
C'est ça ?
Il faudrait un jour d'examen, justifier la relation entre vitesse et vitesse angulaire.
C'est parce que les fils ne glissent pas sur les poulies.
Oui mais la situation est un peu différente des précédentes car le fil, une fois déroulé, reste vertical et immobile.
Ah d'accord j'ai compris.
3) Expression de la vitesse v
Le système étudié est maintenant le solide (S) et la barre (B).
Seul le poids de la barre (B) a un travail non nul. Ensuite, le solide (S) est en rotation, mais la barre (B) est en translation. Donc l'énergie cinétique du système (S)+(B) est la somme de deux énergies cinétiques.
Soit le poids de la barre.
Le TEc donne :
Mais Ec = Ec - Ec0
Or Ec0 = 0 à l'instant initial.
À l'instant final Ec = ½M'v² + ½J.² = 6mv²
Alors le TEc devient : 6mv² = M'gh
Or M' = 3m
D'où 2v² = gh 
Expression de l'accélération a de la barre
Nous avons établis que 2v² = gh
En dérivant cette relation, on obtient ceci :
4.v'.v = gh'
Or v' = a et h' = v
Donc 4av = gv
Merci bien vanoise !
Seul le Seigneur pourra vous récompenser pour tout ce que vous faites pour nous. J'ai un seul mot pour vous tous : Merci !
J'ai appris et continue d'apprendre beaucoup de choses intéressantes et ce, grâce à vous.
Je remercie vraiment le Seigneur de m'avoir fait découvrir ce forum. Merci à vous tous !
Annuler
connectez vous