Inscription / Connexion Nouveau Sujet
Dynamique de rotation 3
Bonjour tout le monde, aidez-moi svp à corriger cet exercice.
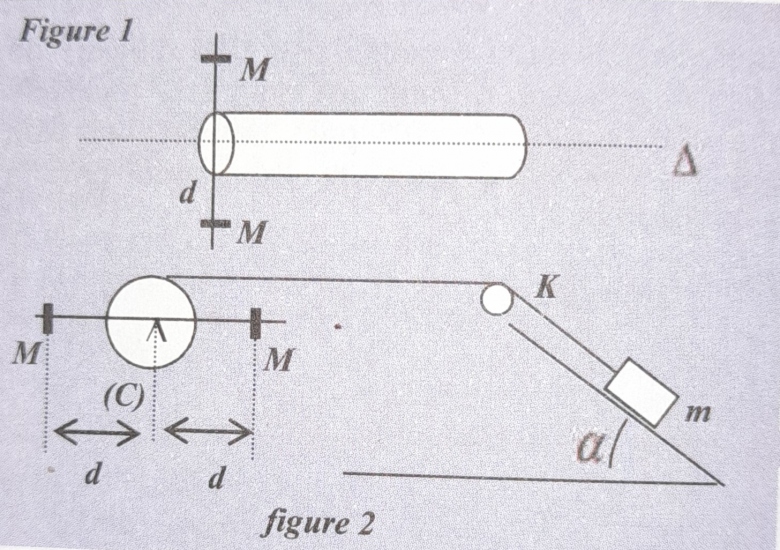
Problème : Soit une tige métallique homogène, de section constante ; cette tige traverse diamétralement un cylindre C d'axe horizontal de rayon r, mobile sans frottement autour d'un axe (
) horizontal (confondu avec l'axe de révolution de C). La tige est munie de 2 masselottes identiques considérées comme ponctuelles de masse M chacune. Ces masselottes sont situées à une même distance d par rapport à l'axe () de rotation (figure 1). Un fil inextensible de masse négligeable est enroulé sur le cylindre. Ce fil passe par ailleurs sur la gorge d'une poulie k (dont on négligera la masse et les frottements sur son axe) et supporte un solide de masse m qui peut se déplacer sur un plan incliné d'un angle 
par rapport au plan horizontal. L'ensemble des frottements sur la masse m se résume en une force unique de même direction que le plan incliné, de sens contraire au mouvement de m et d'intensité f supposée constante. (Figure 2).
On désignera par J le moment d'inertie du système S (cylindre + tige + masselotte), et par J0 le moment d'inertie du système S' (cylindre + tige).
1) Le système ayant été libéré sans vitesse initiale à une date prise comme origine des temps t = 0, on demande d'établir par application des lois de la dynamique l'expression de l'accélération angulaire du système en rotation en fonction de m, r, J0, d, M, f, et g.
2.a) Établir la loi horaire du mouvement de rotation en supposant qu'à la date t = 0 l'abscisse angulaire de la tige est nulle.
b) Sachant qu'elle effectue 4 tours en 0,50 s, calculer son accélération angulaire 
".
3) Afin d'étudier l'influence du moment d'inertie sur le mouvement de la tige, on mesure le temps t qu'elle met pour faire 2 tours pour différentes valeurs de d.
| d(cm) | 6 | 10 | 14 | 18 |
| t(s) | 3,16 | 3,76 | 4,51 | 5,36 |
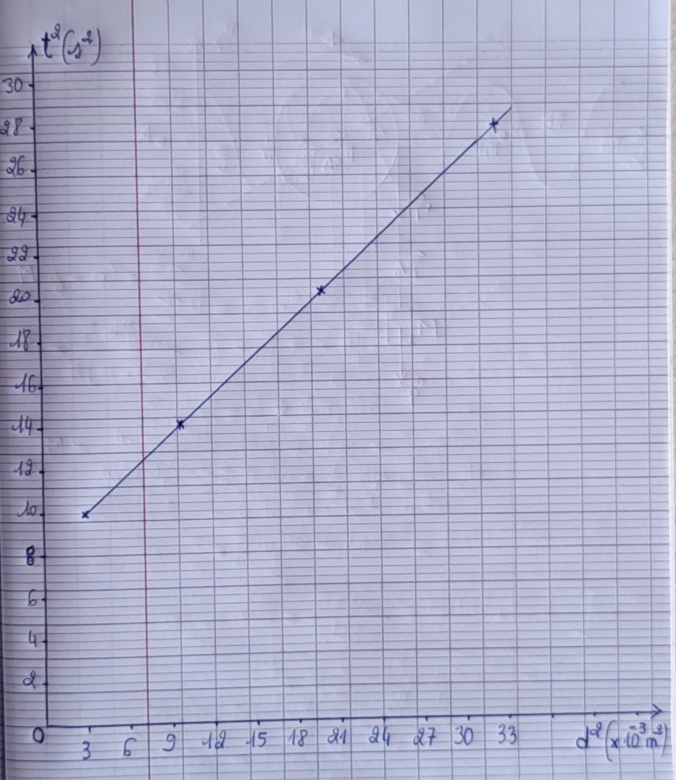
Echelle : 1 cm pour 2,0.10-3 m² ; 1 cm pour 2,0 s².
b) Montrer que la relation littérale liant t² et d² peut se mettre sous la forme t² = ad² + b.
a et b sont des constantes que l'on exprimera en fonction de m, r, J0, M, f,
et g.
c) À partir du graphique, calculer f et J0.
Données : m = 100 g ; g = 9,80 SI ; r = 2,00 cm ; M = 150 g ;
= 60⁰
Bonjour
Que proposes-tu comme expression de l'accélération ? La démonstration est très proche de celle correspondant aux problèmes précédents
Question 1) : expression de l'accélération angulaire
Veuillez vérifier pour moi si mon schéma est propre, puisque la résolution repose essentiellement sur le dessin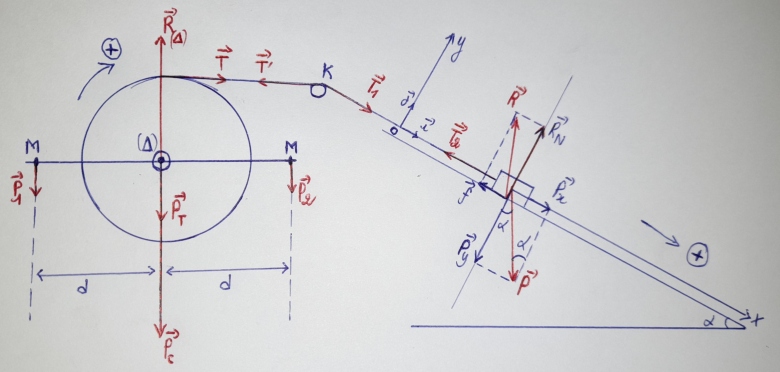
Bonjour
Schéma très soigné !
Juste une simplification possible. Il me semble plus simple de considérer la partie en rotation comme un seul solide dont le centre de gravité est sur l'axe de rotation. Sinon il faudrait faire intervenir les actions de la tige sur les masselottes.
D'accord !
Sur le système en rotation (cylindre + tige), seule la tension du fil travaille.
Le Théorème de l'énergie cinétique est :
Donc Ecf = T.r (Ec0 = 0 à t = 0)
Maintenant ½J0.
² = T.r
A mon avis, la tension T représente la composante du poids sur Ox.
Attention : le théorème de l'énergie cinétique fait intervenir les travaux de toutes les forces dans le cas général même si souvent les travaux des forces intérieures s'annulent deux à deux.
Comme déjà expliqué, tu as deux méthodes possibles :
Théorème de l'énergie cinétique ou théorème de l'énergie mécanique appliqué au système global.
Théorème des moments appliqué au solide en rotation et relation fondamentale de la dynamique appliquée aux deux solides en translation puis prise en compte des tensions des fils. Ici l'énoncé semble préférer la seconde.
Théorème des moments appliqué au solide en rotation et relation fondamentale de la dynamique appliquée aux deux solides en translation puis prise en compte des tensions des fils
Moi je vois un seul solide en translation et non deux. Seul la masse m est en translation. Le cylindre, la tige et les deux masselottes constituent un seul solide en rotation.
Maintenant, si je comprend bien :
• sur le solide en rotation, J'applique le Théorème de l'accélération angulaire, je tire la tension T du brin de fil ;
• sur le solide de masse m en translation, J'applique le Théorème du centre d'inertie, je tire la tension T'.
Ensuite, la masse du fil étant négligeable les tensions de part et d'autre de la poulie k sont égales (T = T')
Donc j'égale les deux expressions je tire
" sachant que a = r."
C'est ça ?
• Sur le système en rotation
= J."
Seule la tension T a un moment non nul
Donc T.r = J." 
T = (J.")/r
Avec J = J0 + 2Md²
• Sur le solide de masse m en translation
Le Théorème du centre d'inertie et projection de la relation vectorielle sur l'axe Ox donne :
mg.sin - T2 - f = m.a
Donc T2 = mg.sin - f - m.a
Avec a = r."
Enfin je pose que T = T2 puis je tire "
Donc (J/r)." = mg.sin - f - m.r."
Alors (J/r + mr)" = mg.sin - f
(J + mr²)" = (mg.sin - f)r
En fin
2.a) Loi horaire du mouvement
" étant une constante, la loi horaire est de la forme :
= ½"t² + 0t + 0
Or à t = 0, 0 = 0 et 0 = 0
D'où
b) Calcul de l'accélération angulaire
La loi horaire de la vitesse angulaire est de la forme
= "t + 0
Avec 0 = 0
Donc " = /t
Mais = 2
N
Ici N = 4/0,50 = 8 tours/s
Ainsi = 16 rad/s.
Maintenant " = 16/t² rad/s²
Mais je ne connais pas t.
D'accord, je continue avec la notation des angles, puisque j'ai commencé par ça.
= ½"t²
Or = 2n ; où n est le nombre de tours.
Donc 2n = ½"t²
AN : " 
201 rad/s²
3.a) On demande à présent de construire le graphe t² = f(d²). Pour cela je dois avoir un tableau de valeurs.
| d²(m²) | 3,6.10-3 | 10.10-3 | 19,6.10-3 | 32,4.10-3 |
| t²(s²) | 9,99 | 14,1 | 20,3 | 28,7 |
Maintenant l'échelle est donnée. Si mon tableau de valeurs est correcte (nombre de chiffres significatifs), je vais procéder au tracé du graphe.
Énoncé pas très cohérent au niveau des chiffres significatifs. Tableau de valeurs avec parfois 3 chiffres significatifs, parfois un seul. Dans ce genre de situation, je conseille d'en fournir 3 même si l'étude graphique,si effectuée sans logiciel type tableur, va te ramener à un résultat final avec 2 chiffres significatifs.
OK.
J'ai placé les points sur le repère, ils sont alignés.
J'ai pas suffisamment de place sur l'axe des abscisses, la graduation manque. Mais j'ai compris quand même que ces points sont alignés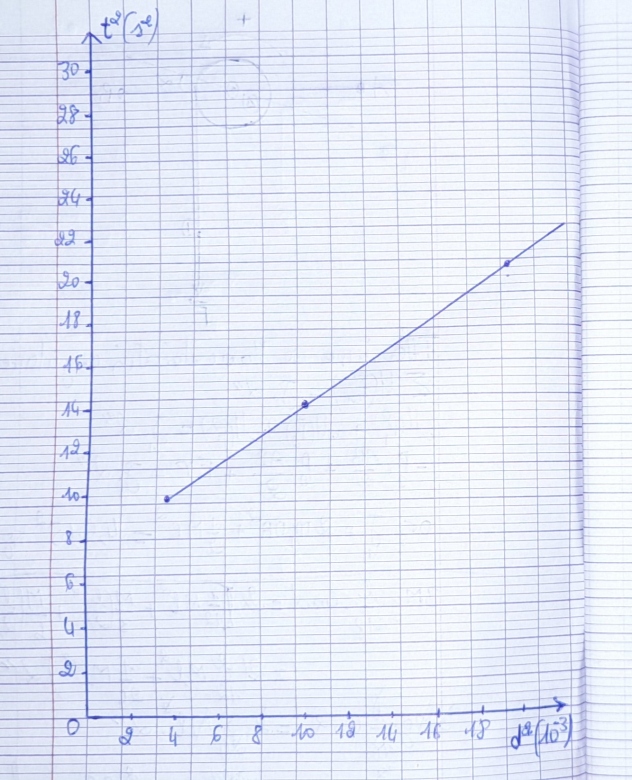 
Tu n'as pas respecté les consignes de l'énoncé sur le choix des échelles. Cela t'aurait permis de placer les quatre points expérimentaux. Équation de la droite moyenne ?
Un point expérimental se représente par une petite croix tracé en traits fins ; pas par un disque de rayon plus ou moins grand qui (pas ici mais le risque existe) peut se transformer en "pâté"...
Pour l'échelle, j'ai pourtant utilisé une règle pour graduer les axes de mon repère. 1 cm représente une unité.
Sur l'axe des ordonnées, chaque cm vaut 2 s².
Sur l'axe des abscisses, chaque cm vaut 2.10-3 m².
Je crois avoir fait cela.
Maintenant pour la représentation des points expérimentaux en croix au lieu en disque je prend bonne note.
Une feuille de papier A4 possède une largeur supérieure à 16,2cm...
Si tu n'utilises pas des feuilles A4 mais des cahiers, tu peux modifier l'échelle en choisissant en abscisse 1cm pour 3.10-3m2
b) L'équation de cette droite est de la forme :
t² = ad² + b.
Maintenant mon soucis c'est comment trouver la pente a et l'ordonnée à l'origine b en fonction des paramètres demandés.
Ici, je dois l'avouer honnêtement je n'ai du tout compris comment même débuter
En utilisant les notations du cours de math, tu obtiens une droite d'équation : y=a.x+b
"b" est l'ordonnée en x=0 ; il suffit de prolonger la droite jusqu'à son intersection avec l'axe des ordonnées pour obtenir graphiquement la valeur de b.
"a" est le coefficient directeur de la droite. On choisit deux point A et B sur la droite (pas nécessairement des points expérimentaux) assez éloignés l'un de l'autre pour une meilleure précision. Alors :
Je préfère, pour ne pas commettre des erreurs, continuer avec les points expérimentaux.
Soit A(9,99 ; 3,6.10-3) et B(28,7 ; 32,4.10-3)
Dans ce cas la pente de la droite est a = 1,54.10-3
L'ordonnée à l'origine est b = 8 (valeur obtenue graphiquement)
Alors t² = 1,54.10-3d² + 8
Mais vanoise, on demande d'exprimer a et b en fonction de m, r, J0, M, f, et g.
Je préfère, pour ne pas commettre des erreurs, continuer avec les points expérimentaux.
Attention : il faut choisir deux points appartenant à la droite moyenne. Si des points expérimentaux sont exactement sur la droite moyenne, tu peux les choisir bien sûr mais choisir des points expérimentaux qui ne sont pas tout à fait sur la droite moyenne entraîne des erreurs.
Tu devrais être capable de fournir deux chiffres significatifs sur b. Es-tu sûr de ta valeur de a ? Mon programme de régression linéaire n'est pas d'accord avec toi !
Tu as déjà exprimé
en fonction de t2. Or, tu as une relation simple entre et "d".Ah d'accord, j'ai trouvé a = 1,53.10-3
Donc t² = 1,53.10-3d² + 8,0
Pour trouver a et b en fonction des paramètres demandés, il faut donc utiliser la relation
C'est ça ?
C'est ça ?
Oui pour ta deuxième question.Concernant l'équation de ta droite moyenne, tu n'as pas tenu compte de mes remarques précédentes. Prenons par exemple le premier point expérimental :
d=6cm ; t= 3,16s.
Si j'utilise ton équation :
t2=1,53.10-3x36.10-4+8
8
Cela ne donne pas (3,16)2s2
De toutes les façons, avec tes valeurs, le terme en 1,53.10-3.d2 est négligeable pour tous les points de sorte que l'on obtient t2
8s2 
d2 ! Il te faut revoir ton équation !vanoise, j'ai repris le calcul de la pente avec les deux points expérimentaux suivants, appartenant à la droite moyenne A(9,99 ; 3,6.10-3) et B(28,7 ; 32,4.10-3), j'ai trouvé ceci :
a = 1,539.10-3
Maintenant, pour trouver l'ordonnée à l'origine, tu m'as dit de prolonger la droite jusqu'à l'intersection avec l'axe des ordonnées, puis lire la valeur correspondante à x = 0. Ce qui fut fait, j'ai trouvé graphiquement que b = 8,0
Je ne vois vraiment pas où j'ai commis d'erreur.
Sur "b" : il ne s'agit pas d'une erreur : je t'ai juste écrit qu'il est possible d'obtenir la valeur avec deux chiffres significatifs. Voici les résultats obtenus avec un programme de régression linéaire. La méthode graphique ne permet pas d'avoir mieux que deux chiffres significatifs mais un seul sur b comme tu obtiens : trop juste !
D'accord, donc mon équation est correcte
t² = 1,539.10-3d² + 8,0
Sinon, quelle est la valeur de "b" avec deux chiffres significatifs ?
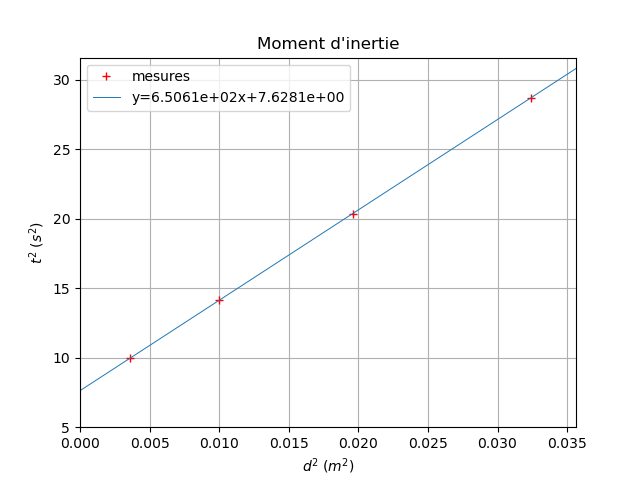
Tu avais corrigé ton erreur sur "a" (avec oubli de l'unité...) dans ton message du 20-07-23 à 16:34 et tu la refais dans ton dernier message. Regarde attentivement la courbe que je t'ai fournie. Les points expérimentaux sont représentés par des croix rouges et la droite moyenne est tracée en bleu clair. Tu peux remarquer qu'elle ne passe pas exactement par les points expérimentaux mais ces points en sont néanmoins très proches. Tu peux donc conclure que la théorie est vérifiée expérimentalement aux incertitudes de mesures près. Le logiciel fournie également l'équation de la droite moyenne avec quatre chiffres significatifs. Impossible graphiquement d'atteindre une telle précision mais avec deux chiffres significatifs, tu peux retenir :
a=6,5.102s2/m2
b=7,6s2
vanoise, je suis vraiment désolé, mais excuse moi, je vais poser mes questions, là où je n'ai pas compris.
• À la 3.a), l'énoncé demande de tracer le diagramme t² = f(d²). Cela est fait !
• Ensuite l'énoncé demande de montrer que la relation liant t² et d² peut se mettre sous la forme : où a et b sont des constantes à exprimer en fonction de m, r, J0, M, f,
et g.
Je crois qu'à ce niveau, comme tu l'as souligné pour trouver a et b en fonction des paramètres demandés, il faut donc utiliser la relation
Pour une question de cohérence dans la notation des angles, je remplace qui se trouve au premier par
Donc
Ce qui donne
Donc l'équation demandée est la suivante :
Où et
• Maintenant est-ce que les valeurs numériques de a et b sont demandées ? Si oui, le calcul de la pente a ne devrait-il pas se baser sur le tableau de valeurs de t² = f(d²) dans mon message du 12-07-23 à 17:52 et non le tableau donné par l'énoncé ?
J'ai posé ces questions parce que nous avons deux valeurs de a différentes : moi j'ai trouvé a = 1,539.10-3s²/m² et toi tu as trouvé a = 6,5.102 s²/m².
Stp, ne te fâche pas, parfois on comprend difficilement.
Il n'y a pas d'erreur dans ton tableau du message du 12-07-23 à 17:52 mais, dans ton raisonnement du 20-07-23 à 00:11, tu as permuté abscisses et ordonnées : t2 est en ordonnées comme tu as fait sur tes graphiques. Dans ces conditions :
Dans la mesure où tu n'utilises pas de papier millimétré, la détermination graphique de « b » est délicate. Je vais considérer que le dernier point expérimental est sur la droite moyenne et j'utilise la valeur de « a » que je viens d'obtenir :
Valeurs tout à fait cohérentes avec les résultats de la régression linéaire que je t'ai fournis : logique puisque les deux points expérimentaux choisis sont très proches de la droite moyenne.
Pour l'étude théorique : tu as raison pour les notations : la notation est réservée pour caractériser la pente du plan incliné. D'accord avec tes valeurs théoriques de « a » et « b ».
D'accord, maintenant j'ai très bien compris ! J'ai permuté abscisses et ordonnées dans le calcul de la pente.
Récapitulons :
Théoriquement
Graphiquement
a 6,5.102 s²/m² et b 7,6 s²
Maintenant, on passe à la dernière question 3.c
À partir du graphique, calculons f et J0 :
Je crois qu'à ce niveau je dois former le système d'équations de a et b de mon étude théorique, puisque leurs valeurs sont connues dans l'étude graphique.
Le seul souci que j'ai, j'obtiens deux équations à trois inconnues : f, J0 et
• Quand je prend le rapport a/b, j'obtiens ceci :
AN : J0 3,5.10-3 kg.m²
Maintenant j'ai du mal à calculer puis f.
L'énoncé précise que le tableau de mesures correspond à une rotation de 2tours. Reste à convertir en radians.
Annuler
connectez vous