Inscription / Connexion Nouveau Sujet
Dynamique,
Bonjour, j'ai besoin d'aide pour cet exercice :
On dispose d'un ressort à spires non jointives de masse négligeable, de raideur k=10 N/m et de longueur à vide lo = 20 cm.Le ressort est enfilé sur une tige AB soudé en A à un axe vertical (A) et inclinée obliquement par rapport à la verticale descendante d'un angle a = 60°. L'une des extrémités du ressort est fixée en A l'autre porte un anneau de masse m = 100g pouvant coulisser sans frottement sur la tige AB. 1°) Le système est au repos.
Calculer la longueur l1 du ressort et la réaction R, de la tige sur l'anneau.
2°) L'ensemble tourne autour de l'axe (A) avec une vitesse angulaire w= 4 rad/s. Déterminer la longueur l2 du ressort et la réaction R₂ de la tige sur l'anneau.
3°) Montrer que la réaction de la tige sur l'anneau peut s'annuler pour une certaine valeur w de la vitesse angulaire que l'on calculera.
Bonjour
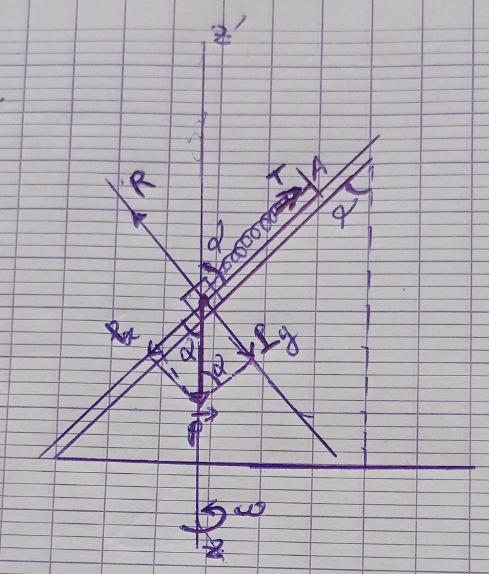
Pour la 2 : commence par faire un schéma propre sur lequel tu représentes les différents vecteurs forces et le vecteur accélération par rapport à la terre. La relation fondamentale de la dynamique conduit alors aux résultats demandés.
Tu peux scanner ton schéma puis le poster sur ce forum.
D'accord avec tes vecteurs force. Manque le vecteur accélération par rapport à la terre du centre G de l'anneau. Tu n'auras plus alors qu'à projeter la relation vectoriel sur deux axes comme tu es habitué à le faire.
vanoise
Sur l'axe normal :
-T+Px =mr(w) ^2
Le problème est que je ne sais pas comment trouver le rayon r en fonction de la longueur L2 de ce mécanisme. Merci de m'assister cordialement
Tes projections prennent en compte une accélération colinéaire au ressort, ce qui est faux. L'accélération est orienté vers le centre de la trajectoire ; ce point est le projeté orthogonal du point G sur l'axe de rotation.
Tu as des équations quasi identiques à celles du pendule conique que tu as étudié récemment ici :
Mouvement pendulaire
vanoise
Pouvez-vous m'aider avec les composantes de l'accélération sur le plan incliné, vu qu'elle n'est pas colinéaire, j'ai du mal à repérer sur le plan incliné,
Merci d'avance
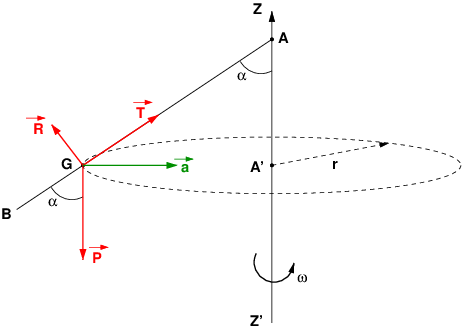
Cette figure devrait t'aider à obtenir les projection sur un axe vertical passant par G et un axe horizontal passant par G et A', le centre de la trajectoire circulaire de G.
Un conseil : évite de faire une figure avec 
=45°. Il est très facile alors sur la figure de confondre l'angle et son complémentaire puisque ces deux angles sont égaux dans ce cas particulier.
vanoise
Bonjour mr, j'ai repris en tenant compte des directives que vous avez énumérées,
J'ai obtenu L2=28,4cm et R2=m(g-w^2cosa)sina=0,67N.
Veuillez vérifier pour moi svp
En projetant sur les deux axes, on obtient :
En multipliant tous les termes de (1) par sin() et tous les termes de (2) par cos(), on obtient :
soit :
On peut obtenir plus simplement et directement cette relation en projetant la relation vectorielle sur un axe colinéaire à la tige (AB) mais puisque la suite du problème s'intéresse aussi à R...
Peut-être un simple problème d'arrondi dans les calculs ; en posant g=9,81m/s2, j'obtiens : l=28,9cm. La relation (2) conduit à :
L'application numérique conduit à R=0,618N.
Annuler
connectez vous