Inscription / Connexion Nouveau Sujet
DM sur les Fentes d'Young
Bonsoir,
Je suis actuellement bloquée sur mon DM de physique, pourriez-vous m'aider à répondre à cette question :
1/ Complétez les valeurs inconnues en abscisse du document 4 (ci-joint) en justifiant ?
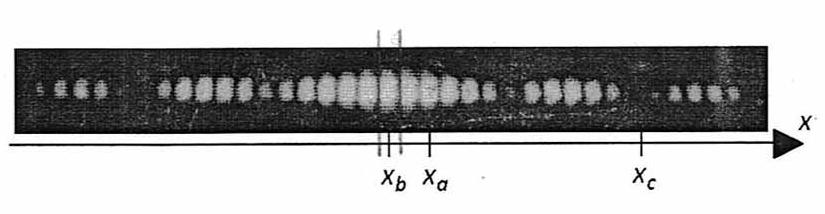
Je ne comprends pas ce que représente Xb ? est-ce la taille de la tâche centrale ?
Cela doit me permettre de calculer Xa et Xc.
Comment faire ? 
Merci,
Abi 
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
C'est encore moi,
Les données ont été effacées sur mon schéma.
Voici ce qu'on a :
> distance écran/fente : 1,5 m
> écartement des deux fentes : b = 200 nanomètres
> longeur d'onde de l'onde monochromatique incidente : lambda = 600 nm
> Xb = 5 cm
> les positions des graduations Xa, Xb, Xc sont représentées à l'échelle.
Bonjour,
Cela serait certainement beaucoup plus clair si tu faisais l'effort de recopier un énoncé exact et complet.
Ce que je lis dans ton deuxième message :
. Xa, Xb, et Xc sont des graduations
. Xb = 5 cm
Cela laisse supposer qu'il y aurait quelque part une origine des abscisses.
La figure que tu as postée n'est-elle pas tronquée vers la gauche ? L'origine sur l'axe des abscisses n'a-t-elle pas disparue, ce qui empêche de déterminer les abscisses Xa et Xc qui sont "représentées à l'échelle" ?

Bonjour,
Mon schéma est entier. C'est justement ce détail qui me semble bizarre. Je ne comprend pas comment je peux calculer les valeurs sans autres informations. J'ai relu "l'énoncé" qui est plutôt une question, et il est en effet complet.
est-ce que le fait que les valeurs soient représentées "à l'échelle" signifie que le schéma est représentatif de la réalité ?
Merci encore.
Abi.
Une autre piste :
Xa - Xb = deux interfranges
Donc... calcule l'interfrange et "étalonne" ainsi l'axe des abscisses...

Oui !
C'est exactement ce qu'ai j'ai fais.
Malgré tout, je ne trouve pas cela exact, puisque si j'en crois d'autres schémas, la longueur de la seconde tâche est égale à la moitié de la tâche centrale (soit 2,5 cm dans notre cas.)
Xb = 5 cm ; donc la longueur de la tâche que pointe Xb = 5 cm. Mais la valeur de Xb devrait être égale à 0 puisqu'elle se situe sur le point le plus intense.
Dans ce cas, Xc = Xb / 2 + 2,5
donc Xc = 2,5 + 2,5
Xc = 5 cm
...
Lorsque je calcule à partir des interfranges, je trouve 5,85 cm ( i = 0,0045 m)
Pourquoi cette différence ?
Je serai d'accord avec la valeur de l'interfrange, à la condition que tu corriges (dans ton message d'hier à 20 h 58) la valeur aberrante de l'écartement des deux fentes.
Sachant cela (et adoptant la valeur 5 cm pour l'abscisse Xb) que vaut l'abscisse Xa ?
Ceci te permet de trouver l'échelle du graphique et donc de déterminer l'abscisse de la graduation Xc
Quand tu connaîtras cette nouvelle abscisse, tu pourras, par exemple, en déduire la largeur d'une fente. (L'énoncé ne te demande-t-il pas cela ? Tu as copié la question 1... il doit bien y avoir d'autres questions...)

(En effet, il s'agissait de 200 micromètres...et non pas 200 nanomètres...  )
)
Donc si on considère en effet que la valeur de Xb est de 5 cm, alors Xa peut être calculé ainsi :
Xa = Xb + (i x 2)
Xa = 5 + (0,45 x 2)
Xa = 5,9 cm
Est-ce bien cela ? Pour le reste, normalement cela devrait aller. J'ai utilisé les formules du cours

Merci pour votre aide


