Inscription / Connexion Nouveau Sujet
DM de Physique : les interférences
bonsoir, je suis entrain de finir mon Dm sur les interférences, mais il me reste 1 dernier exo, et faut savoir determiner si l'onde est destructive ou constructive mais apres de multiple recherche je ne sais pas comment faire
,
En observant une bulle de savon, on voit apparaître des irisations dont les couleurs changent suivant l'angles d'observation. C'est le phénomène d'iridescence.
Une bulle de savon est constituée d'un mince film d'eau savonneuse emprisonnant de l'air. Quand la lumière traverse ce film, il se produit un phénomène d'interférences entre la lumière réfléchie sur la face supérieure du film et celle réfléchie sur la face inférieure. La différence de marche entre ces deux rayons qui interfèrent dans l'oeil est alors donnée par la relation
:  0=2n.e.cos(i2)+(
0=2n.e.cos(i2)+( 0/2)
0/2)
e: épaisseur du film d'eau
n: indice de réfraction du film d'eau
r: angle de réfraction du rayon réfracté dans l'eau : longueur d'onde du rayon incident
: longueur d'onde du rayon incident
donnée: longueur d'onde d'une radiation de couleur rouge ( 0=640nm)
0=640nm)
indice de refraction de l'eau savoneuse: n=1,35nm
1) determiner si les interferences sont constructives ou destructives pour une radiation rouge si l'eppaiseur du film est de: e=0,32um et si l'angle de refraction est de i2=42°
si vous pourriez m'aider ca serai super sympa de votre part
merci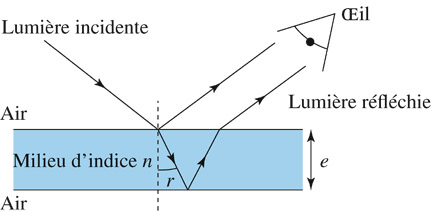
***Titre complété pour plus de clarté***
je pense avoir trouver mais je ne suis pas sur... voici mon resultat
on prend k = 1,35 soit
 =2n.e+(
=2n.e+( /2)
/2)
<=> k* = 2n.e+(
= 2n.e+( /2)
/2)
<=> =2n.e+(
=2n.e+( /2)
/2)
<=> - (
- ( /2) = 2n.e
/2) = 2n.e
<=>  /2 = 2n.e
/2 = 2n.e
<=> e = /(4n)
/(4n)
et apres je fais l'AN
Bonsoir,
Fais nous part de quelques unes de tes multiples recherches pour qu'on puisse voir ou tu en es.
Bien entendu, je suppose que tu as appris ton cours et que, pour des interférences, tu sais à quelle condition 2 ondes sont constructives et à quelle condition elles sont destructives.
Merci de rappeler ces conditions dans ta réponse.
merci d'avoir repondu, je viens de poster juste avant votre message une reponse que j'ai trouvé, mais j'en suis pas sur
Nos posts se sont croisés.
Je renouvelle ma question sur les conditions pour lesquelles 2 ondes sont constructives ou destructives.
si 2 ondes sont en phase elles sont constructives
et si elles sont en opposition de phase elles sont destructive
Bon ... alors je précise ma question :
A quelle condition portant sur la différence de marche a t'on des ondes constructives ?
Même question pour des ondes destructives
ahh désolé
si l'amplitude de l'onde est maximale L'interférence est constructive . et elle sera minimale pour la destructive
je sais pas si j'ai repondu a la question
Non.
La première chose à faire est de revenir à ton cours et d'y rechercher les conditions dont je te parle.
Tu les trouveras aussi ici ( paragraphe III, sous paragraphe 3) ![]() Les interférences
Les interférences
ok merci je viens de lire, et ceci ne figure pas dans mon cours mais ca maide beaucoup Une frange brillante en un point M correspond à une amplitude de la vibration résultante maximale et égale à 2A. constructive
Une frange sombre en un point M correspond à une amplitude de la vibration résultante minimale et égale à 0. destructive
mais comment cela va m'aider pour résoudre la question??
Apparemment tu n'as toujours pas compris mes questions. ( Voir mon post du 18-10-20 à 23:58 )
Je les répète :
A quelle condition portant sur la différence de marche, deux ondes donnent elles une interférence constructive ?
A quelle condition portant sur la différence de marche, deux ondes donnent elles une interférence destructive ?
Rebonjour, je ne trouve pas dans le paragraphe III, sous paragraphe 3, le sujet sur la différence de marche, il n'y a que les définitions des ondes constructive et destructive, je pense que c'est dans le sous paragraphe 2
Je pense avoir trouver
Si  = n x
= n x avec n entier, les interference sont constructive
avec n entier, les interference sont constructive
Si  = (2n+1)
= (2n+1)  /2 les interference sont destructive
/2 les interference sont destructive
Il s'agit bien du paragraphe III, sous paragraphe 3, alinéas b et c
La différence de marche y est notée  geo
geo
Ce  geo correspond au
geo correspond au  0 de ton énoncé.
0 de ton énoncé.
Bien entendu ce que tu as fait est faux puisque tu ne t'es pas servie des conditions que tu exposes dans ton post du 19-10-20 à 11:47
Je reprends :
Si la différence de marche est égale à un nombre entier de longueurs d'ondes ( donc δ0 = n*λ ) alors les interférences sont constructives.
Si la différence de marche est égale à un nombre impair de demies longueurs d'ondes ( donc δ0 =(2n+1) *λ/2 ) alors les interférences sont destructives.
Ton exercice se résume donc à calculer la valeur numérique de la différence de marche et à rechercher ensuite dans lequel des deux cas on se trouve
Donc je dois faire le calcul suivant:
δ0 = n*λ
= 1,35*640
= 864
c'est un nombre entier donc c'est une interférence constructive
δ0 =(2n+1) *λ/2
= (2*1,35+1)*640/2
= 1184
c'est un chiffre pair donc c'est une interférence constructive
c'est bien cela?
Non
La différence de marche se calcule à partir des données de l'énoncé :
La différence de marche entre ces deux rayons qui interfèrent dans l'oeil est donnée par la relation
 0 = 2n . e. cos(i2) + (
0 = 2n . e. cos(i2) + ( 0/2)
0/2)
ok
 0 = 2n . e. cos(i2) + (
0 = 2n . e. cos(i2) + ( 0/2)
0/2)
= 2*1,35*0,32*cos(42°)+(640/2)
= 319.65
donc ce n'est pas un nombre entier, alors ce n'est pas une interférence constructive
C'est bien cela??
Pour commencer, il faut être attentif à la question des unités :
" n" est un indice de réfraction qui n'a pas d'unité ( bien que ton énoncé prétende que c'est une longueur !)
n = 1,35
" e " est une longueur qui doit être exprimée en m
" cos( i2) " n'a pas d'unité. i2 = 42°
"  0 est une longueur d'onde donc c'est une longueur qui doit être exprimée en m
0 est une longueur d'onde donc c'est une longueur qui doit être exprimée en m
Ton calcul est donc à revoir.
Une fois ton calcul terminé, cherche si son résultat est oui ou non égal à un nombre entier de longueurs d'ondes (et pas si ce résultat est lui même un nombre entier comme tu sembles le penser)
Enfin cherche si ce résultat est oui ou non égal à un nombre impair de demies longueur d'ondes.
Tu pourras alors conclure, si l'interférence est constructive ou destructive.
d'accord j'applique cela
 0 = 2n . e. cos(i2) + (
0 = 2n . e. cos(i2) + ( 0/2)
0/2)
=2*1,35*3,2e-7*cos(42°)+(6,4e-7/2)
=-2,558e-8
mais je ne sais pas ce que c'est qu'un nombre entier de longueurs d'ondes, ni nombre impair de demies longueur d'ondes.
J'ai regardé sur le liens que vous m'avez montrer mais je ne trouve pas...
Un simple coup d'il montre que ton calcul est faux et en plus rendu sans unité !
En effet, en multipliant ou en additionnant des quantités toutes positives, il est impossible de trouver un résultat négatif.
Je soupçonne ta calculatrice de travailler avec des angles en radians. A vérifier.
Quand tu auras le résultat ( avec son unité ! ! ! ) :
Combien y a t'il de longueurs d'ondes dans ce résultat ? ( Un nombre entier oui ou non ? )
Combien y a t'il de demies longueurs d'ondes dans ce résultat ? ( Un nombre impair oui ou non ) ?
Non.
Encore une fois tu rends un résultat sans son unité
Je vais préparer ce calcul :
n = 1,35
e = 0,32 µm = 3,2 . 10-7 m
i2 = 42° ; cos(i2) = 0,743
 0 = 640 nm = 6,4 . 10-7 m
0 = 640 nm = 6,4 . 10-7 m
 0 = 2n . e. cos(i2) + (
0 = 2n . e. cos(i2) + ( 0/2) = .....................
0/2) = .....................
Je te laisse terminer et rendre un résultat accompagné de son unité
Non ...
Le calcul correctement posé est :
 0 = 2 * 1,35 * 3,2 . 10-7 * 0,743 + (6,4 . 10-7) / 2
0 = 2 * 1,35 * 3,2 . 10-7 * 0,743 + (6,4 . 10-7) / 2
 0 = ................
0 = ................
Même si tu ignores l'unité de différence de marche (ce qui montre une profonde méconnaissance du cours) tu peux facilement retrouver cette unité à partir des unités utilisées dans le calcul
D'accord merci beaucoup de m'aider
voici le resultat: 23.48 m (je viens de retrouver l'unité est en mètres)
et apres " Combien y a t'il de longueurs d'ondes dans ce résultat ? " je n'est pas compris ce que ca veut dire
L'unité de différence de marche est bien le mètre.
Si tu connais la valeur de la différence de marche ( en m ) ainsi que la valeur de la longueur d'onde ( en m également ) alors il est à la portée d'un élève de collège de calculer le nombre de longueurs d'ondes comprises dans la différence de marche.
Mais il y a un problème qui persiste :
La différence de marche n'est pas égale à 23,48m
J'ai trouvé une valeur des millions de fois plus petite.
ok je viens de refaire le calcul et j'ai trouvé 9,61952e-7 m et 961,952 nm enfin je pense qu'il faut faire ça
j'ai vraiment pas compris la question, ca veut dire quoi de calculer le nombre de longueurs d'ondes comprises dans la différence de marche? je dois regarder c'est équivalent a quelle longueur d'onde?? mais 961nm c'est l'infrarouge
enfin j'ai vraiment pas piger ce qu'il fallait faire
La différence de marche  0 = 962 nm est la bonne réponse.
0 = 962 nm est la bonne réponse.
On dirait que tu penses que cette différence de marche est une longueur d'onde !
Tu as vraiment de très grosses lacunes sur ce chapitre que je te conseille de revoir de fond en comble.
Il s'agit, pour les interférences constructives, de calculer combien de longueurs d'ondes
(  0 = 640nm ) sont comprises dans la différence de marche (962nm)
0 = 640nm ) sont comprises dans la différence de marche (962nm)
Le nombre obtenu est il entier ? Conclusion ?
Ensuite, Il s'agit, pour les interférences destructives, de calculer combien de demies longueurs d'ondes
(640/2 = 320 nm) sont comprises dans la différence de marche (962nm)
Le nombre obtenu est il impair ? Conclusion ?
je vais faire plusieurs exo pour mieux comprendre, mais déjà votre aide me permet de mieux comprendre mon cours, merci beaucoup
je commence a comprendre, mais je ne sais pas comment calculer combien de longueurs d'ondes sont comprises dans la différence de marche, j'en ai aucune idée
Mais bien sûr que tu sais faire ce calcul simplissime.
C'est un peu comme si on te demandait (par exemple) combien de fois 100m sont contenus dans 1800m, puis si on te demandait si le résultat est (ou n'est pas) un nombre entier.
ok voila ce que j'ai fait:
962/640= 1,5
donc ce n'est pas un nombre entiers
et puis 962/320= 3
c'est un nombre impaire donc c'est une interférence destructive
dans la question b) on me dit "proposez une épaisseur de film pour que la bulle apparaissent rouge avec le même angles de réfraction"
donc en gros pour cela je dois avoir une interférence constructive en changent seulement la valeur de e ??
Bonjour, je viens de resoudre la 1ere question de mon Dm grace a un utilisateur de ce site et je le remercie, mais il me reste une derniere question et je sais pas si j'ai bon
En observant une bulle de savon, on voit apparaître des irisations dont les couleurs changent suivant l'angles d'observation. C'est le phénomène d'iridescence.
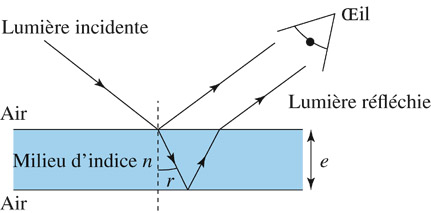
Une bulle de savon est constituée d'un mince film d'eau savonneuse emprisonnant de l'air. Quand la lumière traverse ce film, il se produit un phénomène d'interférences entre la lumière réfléchie sur la face supérieure du film et celle réfléchie sur la face inférieure. La différence de marche entre ces deux rayons qui interfèrent dans l'oeil est alors donnée par la relation
 0=2n.e.cos(i2)+(0/2)
0=2n.e.cos(i2)+(0/2)
e: épaisseur du film d'eau
n: indice de réfraction du film d'eau
r: angle de réfraction du rayon réfracté dans l'eau
 : longueur d'onde du rayon incident
: longueur d'onde du rayon incident
donnée: longueur d'onde d'une radiation de couleur rouge ( 0=640nm)
0=640nm)
indice de refraction de l'eau savoneuse: n=1,35nm
1) determiner si les interferences sont constructives ou destructives pour une radiation rouge si l'eppaiseur du film est de: e=0,32um et si l'angle de refraction est de i2=42°
c'est cette question que j'ai réussi grâce a ujn utilisateur du forum (merci énormément)
voici ce qu'ont a trouver:
 0 = 2 * 1,35 * 3,2 . 10-7 * 0,743 + (6,4 . 10-7) / 2
0 = 2 * 1,35 * 3,2 . 10-7 * 0,743 + (6,4 . 10-7) / 2
=9,61952e-7 m
= 962nm
962/640= 1,5
donc ce n'est pas un nombre entiers
et puis 962/320= 3
c'est un nombre impaire donc c'est une interférence destructive
maintenant voici la Q2:
proposez une épaisseur de film pour que la bulle apparaissent rouge avec le même angles de réfraction
et je pense que pour cela je dois chercher une interférence constructive en changent seulement la valeur de e
c'est bien cela??
*** message déplacé ***
Bonsoir,
Le multi-post est strictement interdit sur le forum  :
:
Tu reçois déjà une aide de la part d'odbugt1, tu continues donc l'échange ici ...
C'est une bien mauvaise idée que celle qui consiste à débiter un énoncé en tranches comme si c'était un saucisson !
A l'issue de ton post du 20-10-20 à 16:20 j'ai pensé que l'exercice était résolu et je suis passé à autre chose.
L'idée que tu proposes dans ton post du 20-10-20 à 16:35 est bonne.
Toutefois, si ton exercice n'était toujours pas terminé après cette question b) je ne continuerai pas à le gérer faute de temps ( en ce moment je ne peux pas toujours traiter simultanément plusieurs topics et je donne la priorité aux énoncés complets)
désolé pour le dérangement mais vu que j'avais aucune réponse j'ai fait un autre post,
Mais voici ce que j'ai fait:
 = 2 * 1,35 * 1,6 . 10-7 * 0,743 + (6,4 . 10-7) / 2
= 2 * 1,35 * 1,6 . 10-7 * 0,743 + (6,4 . 10-7) / 2
=6,40e-7 m = 640nm
640/640=1 donc c'est une interferance constructive et puis si je fait:
640/320= 2 donc pas impaire
donc il faut une épaisseur de 0,16um
0,16µm ( soit 160 nm ) est une bonne réponse, mais elle n'est pas unique :
Les interférences constructives vérifient la relation :
δ0 = k λ0
donc
2 n e cos (i2) + ( λ0 / 2)= k λ0
soit e = [ (k - 1/2) λ0 ] / ( 2 n cos(i2))
Numériquement cela donne ( en nm ):
e = 320 ( k - 1/2 )
Pour k=1 on retrouve e = 160nm
Il serait intéressant d'explorer les autres valeurs entières possibles de k
Merci beaucoup!!
Apres pour la dernière question il n'y a aucun calcul on demande seulement
"pourquoi est il possible de voir différentes couleurs sur une bulle de savon"
et la réponse est:
car la lumière est décomposée à cause de l'épaisseur de la couche d'eau savonneuse : c'est le phénomène de diffraction. En fonction de l'épaisseur de la couche d'eau savonneuse, on voit une couleur plutôt qu'une autre


 ) :
) :

