Inscription / Connexion Nouveau Sujet
DM de physique : 3eme loi de Kepler pour une orbite circulaire
Bonjour, voici l'énoncé de mon exercice
Dans les données astronomiques, on peut lire la masse de différents astres mais aucune balance n'est assez grande pour peser la Terre, le Soleil ou encore une galaxie ! Comment les astronomes arrivent-ils à obtenir ces valeurs?
Les planètes du système solaire gravitent autour du Soleil sur des orbites quasi circulaires. (En fait des ellipses dont l'excentricité e est faible).
1. Considérons la lune point quel référentiel est le plus approprié pour faire l'étude du mouvement de cet astre ?
2. Faire le bilan des forces qui agissent sur la Lune
3. En appliquant la seconde loi de Newton dans le repère de Frénet virgule montrer que la vitesse v de la lune et constante. Comment qualifier le mouvement ?
4. En déduire la vitesse v en fonction de G, mT (masse de la Terre) et du rayon R de l'orbite de la lune.
5. La lune fait le tour de la terre en une période T = 27, 32 jours. Quelle relation lie v, R et T ? En déduire alors la troisième loi de Kepler pour les mouvements circulaires et calculer la masse de la Terre point
Donner deux. G = 6,67 x 10-¹¹ N.kg-²m² et R= 384 000km
Mes réponses:
1. Le référentiel le plus approprié est le référentiel géocentrique que l'on suppose galiléen le temps de l'expérience
2. La force qui s'exerce sur la Lune est la force gravitationnelle [je ne parvient pas a le justifier correctement] .
Je n'arrive pas à faire les questions 3,4 et 5. Si quelqu'un pouvait m'aider et m'expliquer ça serait très gentil. Merci d'avance 
Bonjour,
Questions 1 et 2 : OK
Question 3 :
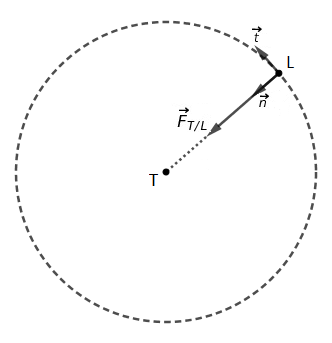
Voir schéma.
Soient MT et ML les masses de la Terre et de la Lune.
Soit R la distance Terre / Lune de centre à centre et V le module de la vitesse de la Lune.
2e loi de Newton appliquée à la Lune :
Loi de gravitation universelle :
Donc :
Expression de l'accélération dans le repère de Frenet :
Je te laisse continuer.