Inscription / Connexion Nouveau Sujet
Distance Terre-Lune et Relativité du temps
Bonsoir à tous .j'espère que vous pourriez m'apporter votre aide pour faire cet exo je suis complètement perdu.
Voici l'énoncé
On se propose de retrouver la relation entre les durées mesurées dans 2 référentiels galiléens. Pour mesurer la distance Terre-Lune, on envoie d'une station d'observation terrestre de puissantes impulsions laser vers un réflecteur qui a été déposé sur le sol lunaire par des spationautes. On mesure, dans la même station au sol, la durée d'un aller-retour de l'impulsion lumineuse. ON imagine qu'un vaisseau spatial se dirige vers le centre de la Terre avec une vitesse v constante de valeur non négligeable devant c, et normale à la direction Terre-Lune. On considère que le système Terre-Lune constitue pendant la durée de la mesure, un référentiel galiléen R.
1)Représenter sur un schéma le trajet du faisceau de lumière de lumière utilisé pour la mesure dans le référentiel R puis dans le référentiel R'.
2) Exprimer la durée delta t de l'aller-retour de l'impulsion lumineuse dans le référentiel R, en fonction de c et de la distance Terre-Lune, notée D
3) Dans le référentiel R' du vaisseau, quelle est la vitesse de propagation de l'impulsion lumineuse ?
4) On admet que a distance D qui est mesuré perpendiculairement à v a la même valeur dans les 2 référentiels. Montrer, que pour respecter les postulats de la relativité restreinte, il faut admettre que la durée delta t' de l'aller-retour de l'impulsion mesurée dans R' est supérieur à delta t
5) Exprimer en fonction de c, v, delta t et delta t' les distances .
6) Etablir la relation entre delta t et delta t'.
3) Dans le référentiel R' du vaisseau, quelle est la vitesse de propagation de l'impulsion lumineuse ?
La vitesse de propagation de l'impulsion lumineuse est égale à c car les deux référentiel sont galiléens
Pour la question
2) Exprimer la durée delta t de l'aller-retour de l'impulsion lumineuse dans le référentiel R, en fonction de c et de la distance Terre-Lune, notée D.
je cherche delta t de l'aller-retour = à un temps
en fontion de c une vitesse et D une distance
Donc Delta t= D/c
Et puisque je veux delta t de l'aller-retour
Delta t= (D/c)^2
Bonjour,
Question 2
Si tu nommes 
t tout d'abord la durée de l'aller, puis ensuite la durée de l'aller et retour, tu prends de grands risques d'erreur. Je te conseille de modifier tes notations pour les rendre cohérentes.
La dernière ligne du message de 17 h 16 est tout à fait fausse. Relis bien !
"La dernière ligne du message de 17 h 16 est tout à fait fausse. Relis bien ! "
donc c'est (Delta t)^2= (D/c)^2
Je pense que tu as commencé par la question 1...
Le schéma doit te montrer comment utiliser le théorème de Pythagore.
"Questions 4 à 6 : le théorème de Pythagore ! "
SVP dites moi un peu plus je n'ai que ce soir pour terminer l'exo
C'est dans le référentiel R que la lumière a un trajet de longueur D à parcourir pour l'aller ; et donc 2D pour l'aller et retour.
Mais la lumière a un trajet beaucoup plus long à parcourir dans le référentiel R'
Tu as mis cela en évidence avec les schémas de la question 1
Pythagore !
Longueur du trajet pour l'aller et retour dans le référentiel R : 2D
La vitesse de la lumière étant c dans ce référentiel R, durée nécessaire pour l'aller et retour :
____________
Durée pour l'aller et retour dans le référentiel R' : t'
Longueur du trajet pour l'aller et retour dans le référentiel R' : (Pythagore)
La vitesse de la lumière étant c dans ce référentiel R', la longueur de l'aller et retour est également c.t'
Donc :
On en déduit :
d'où
et donc, la relation connue :
Mais "recopier sans comprendre est inutile".
"Longueur du trajet pour l'aller et retour dans le référentiel R' : \large 2\sqrt{D^2\,+\,(\frac{v.\Delta t'}{2})^2} (Pythagore)"
cette formule c'est du cours? c'est la première que j'y suis confronté
Non, ce n'est pas du tout du cours (enfin, c'est du cours au collège en quatrième...). C'est l'application du théorème de Pythagore au schéma de la première question.
Question 1 :
En rouge le trajet du faisceau laser dans son aller de la Terre T à la Lune L
En vert (pourquoi pas...) le faisceau réfléchi dans son trajet retour de la Lune vers la Terre.
Le schéma dans le référentiel R de la Terre :
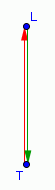
Le schéma dans le référentiel R' du vaisseau spatial qui se rapproche de la Terre :
______________
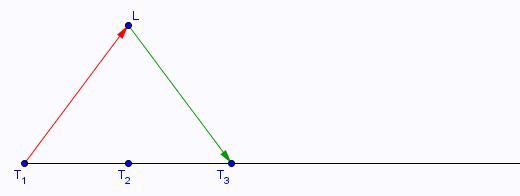
Mon opinion ?
Tu cherches d'abord à te raccrocher à une "formule". Or la physique n'est pas d'abord une question de "formules"
La physique est une manière de décrire la nature, le monde qui nous entoure. Et, parmi les bonnes manières de commencer tout problème de physique, il y a la réalisation d'un schéma qui montre que l'on n'est pas dans l'abstrait mais dans le concret.
Tout d'abord merci de m'avoir aider c'est sympa.
Si je veux appliquer une formule dans un exo il faut bien savoir d'où il vient.
Il faut chercher à comprendre pourquoi elle et pas une autre.
Cette formule n'est pas aussi simple que ça à maitriser or je pense avoir compris
son origine.
En 4ème on apprend le théorème Pythagore sous cette forme AB²+AC²=BC²
La forme que tu cites est lié à un triangle tout à fait particulier : un triangle ABC rectangle en A
Mais on apprend aussi "Le carré de l'hypoténuse est égal à la somme des carrés des côtés de l'angle droit", qui est une forme qui convient parfaitement ici.
Bonjour Coli,
Je suis perplexe devant ton schéma : la fusée se rapproche de la terre. Cette dernière se déplace donc, dans le référentiel R' de la fusée, vers la fusée et non de gauche à droite de celle-ci !
Du coup, si on ne tient pas compte de la contraction des distances (l'énoncé nous dit de ne pas en tenir compte), le trajet est identique dans les deux référentiels.
Ai-je raison ou y a-t-il quelque chose qui m'échappe ?
Bonjour marc73
Voici un schéma qui te conviendra, je pense :
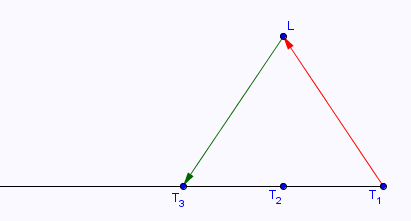
Mais il y a encore des "choses qui t'échappent"
Ce n'est pas parce que l'énoncé le dit qu'il n'y a pas à tenir compte d'une contraction des longueurs de la distance D (cette distance est perpendiculaire à la vitesse du vaisseau, cela l'énoncé le dit très bien).
Eh non, les trajets ne sont vraiment pas identiques dans les deux référentiels.
Encore une fois, il y a peut-être quelque chose qui m'échappe, mais pour moi, le schéma du référentiel R devrait être également celui du référentiel R' : la terre ne se déplace pas dans le référentiel R' de gauche à droite, mais vient vers la fusée ! Il en est de même pour la lune ! La distance apparente (distance angulaire) D augmente puisqu'on se rapproche du rayon laser, donc la distance apparente augmente au fur et à mesure de l'expérience mais elle reste dans la même droite : la fusée avance dans le plan du rayon laser et non perpendiculairement à ce plan ! Il me semble que ton dessin correspondrait à une fusée qui fait le tour de la terre au niveau du plan de l'équateur à vitesse v, par exemple.
Il me semble évident que delta t' < delta t car le temps que le rayon laser met pour arriver à la fusée diminue au fur et à mesure que la fusée se rapproche et cet effet l'emporte sur la dilatation des durées mesurées dans la fusée.
Voici le calcul : delta t' avant de tenir compte du rapprochement de la fusée = delta t x 1/(1-v²/c²)exp 1/2
Rapprochement de la fusée pendant cette durée = idem x v
Gain en temps correspondant sur la réception du signal = idem x v/c
Donc delta t' réel = delta t x 1/ (1-V²/C²)exp 1/2 - (delta t x 1/ (1-V²/C²)exp 1/2) x v/c
= delta t x (1 - v/c) / (1-v²/c²) exp 1/2
PS : pour la contraction des distances, tu n'en tient pas compte dans tes calculs du 19/1 à 21h48 : dans le référentiel R', tu prends bien D et non D'< D pour la distance terre-lune.
Bonjour Coll,
Je suis actuellement en classe de terminale S et j'ai comme travail un dm, dont cet exercice à rendre.
En effet, 3 ans après ce sujet, j'aurai besoin de ton aide afin de m'éclaircir à propos de ce fameux théorème de Pythagore.
Je n'arrive pas à démontrer pourquoi la durée delta T' est supérieur à celle de delta T.
En éspérant une répond dans les plus brefs délais.
Have a nice day!
Bonsoir
Tout a deja ete explique par coll il y a 3 ans
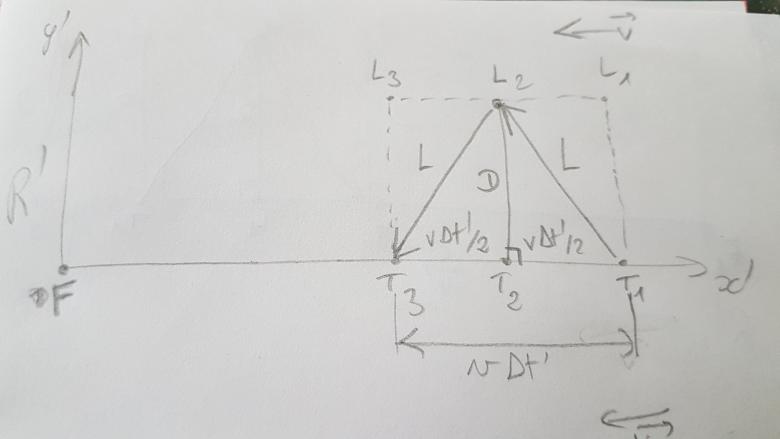
Je poste un schema un peu plus detaille de la situation telle qu'elle est vue dans R ' cad par rapport a la fusee F
(T1,T2,L2) et (T3,T2,L2) etant des triangles rectangles , pythagore n'est plus tres loin😁
Annuler
connectez vous