Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Distance focale et grandissement

Posté par
zazi009B 23-09-12 à 12:10

Bonjour, je suis élève en terminale.
J'ai un problème que je n'arrive pas à résoudre, vous serez t-il possible de m'aider svp?
Voici, le contenu de mon exercice : "On fait tomber un faisceau de rayons parallèles à l'axe sur une lentille divergente de diamètre d. En déplaçant en arrière de la lentille un écran perpendiculaire à l'axe, on obtient une tache lumineuse de forme circulaire; son diamètre est le double de d lorsque l'écran est à 30 cm de la lentille. Quelle est la distance focale de celle-ci?"

J'ai réalisé un schéma. j'obtient deux triangles rectangles colés.La premiète tangente à l'hypoténuse est l'axe principale qui s'étend de F' à l'écran (il comprend OF', OF et les 30cm). L'autre tangente à  l'hypoténuse est d.

J'ai essayé de calculer la distance focale à l'aide de la formule de grandissement. C'est à dire : 1/f = A'B'/AB. Ainsi, j'obtiens 1/d + 1/2d = 1/f. Mais sans jamais arriver au bout de mon problème.
Merci de m'aider à comprendre cette exercice

Posté par
Marc35re : Distance focale et grandissement 23-09-12 à 13:25

Bonjour,
Il faut utiliser le théorème de Thalès (ou les triangles semblables).

Posté par
zazi009BDistance focale et grandissement 23-09-12 à 14:21

En fait en regardant mon schéma, je ne vois pas comment je peut utiliser le théorème de Thalès puisque les triangles ne se touchent pas par le sommet. Tout deux forment comme un triangle isocèle (ceci n'est qu'une image) divisé en deux triangles rectangles.

Posté par
Marc35re : Distance focale et grandissement 23-09-12 à 17:16

Il suffit de considérer les parallèles OL et HE et les sécantes OH et OE (on ne s'occupe pas de OE).
Que peut-on écrire alors ?

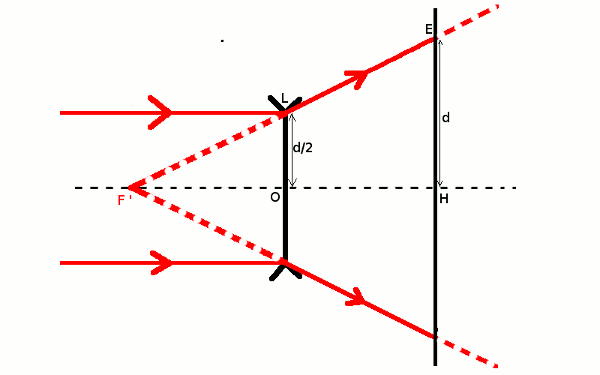
Distance focale et grandissement

Posté par
zazi009BDistance focale et grandissement 23-09-12 à 20:06

Ainsi, d'après l'énoncé OH mesure bien 30 cm ou pas?
parce que si c'est oui, on obtient : OL/HE = F'O/F'H; (d/2)/d = F'O/30. Puis on fait le produit en croix et on obtient  : (d/2 * 30)/d = F'O. Cependant, il me semble que l'énoncé demande une valeur (un nombre) alors que l'on obtient un résultat avec des lettres..

Posté par
zazi009BDistance focale et grandissement 23-09-12 à 20:15

Sinon, est -il possible que j'obtienne ceci? : (d/2)/d=F'O:30 ; (d/2*30)/d =F'O ; (d/2 * 30)/d ; on fait le produit en croix : (d*30)/(d*2) = 15cm.

Posté par
Marc35re : Distance focale et grandissement 23-09-12 à 21:07

\frac{OF'}{OL}\,=\,\frac{HF'}{HE}

OF'\,=\,\frac{OL}{HE}\,HF'

OF'\,=\,\frac{HF'}{2}\,

2\,OF'\,=\,HO\,+\,OF'

OF'\,=\,HO\,=\,0,3\,\,m

Posté par
zazi009BDistance focale et grandissement 23-09-12 à 21:51

Merci pour votre aide, mais je n'arrive pas à comprendre le sens de votre calcul car je n'ai jamais utilisé le théorème de Thalès de cette manière. Pour moi, il faut toujours que FL soit sur FE ou inversement, mais qu'il ne peut pas y avoir OF'/OL...

Posté par
Marc35re : Distance focale et grandissement 23-09-12 à 23:34

Oups, j'ai fait ça un peu vite...
Le théorème de Thalès, correctement appliqué, donne :
\large \frac{OF'}{HF'}\,=\,\frac{OL}{HE}\,=\,\frac{F'L}{F'E}
Ce qui nous intéresse, c'est :
\large \frac{OF'}{HF'}\,=\,\frac{OL}{HE}
\large OF'\,=\,HF'\,\frac{OL}{HE}
\large OF'\,=\,\frac{HF'}{2}
\large 2\,OF'\,=\,HO\,+\,OF'
\large OF'\,=\,HO\,=\,0,30\,\,m

Posté par
zazi009BDistance focale et grandissement 24-09-12 à 17:52

une fois le théorème appliqué correctement, je comprend tout de suite mieux, merci pour votre aide

Est-ce que je pourrais encore abuser de votre temps pour une petite question?
En fait que je ne comprend pas si on me parle d'une lentille convergente ou divergente dont on me parle dans cet exercice : "Une lentille placée à 25

Posté par
zazi009BDistance focale et grandissement 24-09-12 à 17:53

...cm d'un objet en donne une image qui se forme sur un écran placé à 1m de la lentille. Quelle est la distance focale de cette lentille?"

Posté par
zazi009BDistance focale et grandissement 24-09-12 à 17:55

*(En fait que je ne comprend pas si on me parle d'une lentille convergente ou divergente dans cet exercice)

Posté par
Marc35re : Distance focale et grandissement 24-09-12 à 19:15

Peu importe... Tu appliques la relation de conjugaison et, selon le f' que tu vas trouver, tu le sauras...

Posté par
zazi009BDistance focale et grandissement 25-09-12 à 16:37

merci


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !