Inscription / Connexion Nouveau Sujet
dipôle RL
Bonjour, j'aurais besoin d'aide pour cette exo.
Partie A
On alimente le dipôle "bobine résistance R" par un générateur basse fréquence en série avec une résistance Rg de l'ordre de 1k
. Aucune des bornes de sotie du générateur n'est reliée à la masse. La mesure de la résistance de la bobine donne r= 8,0 et R est une résistance variable.
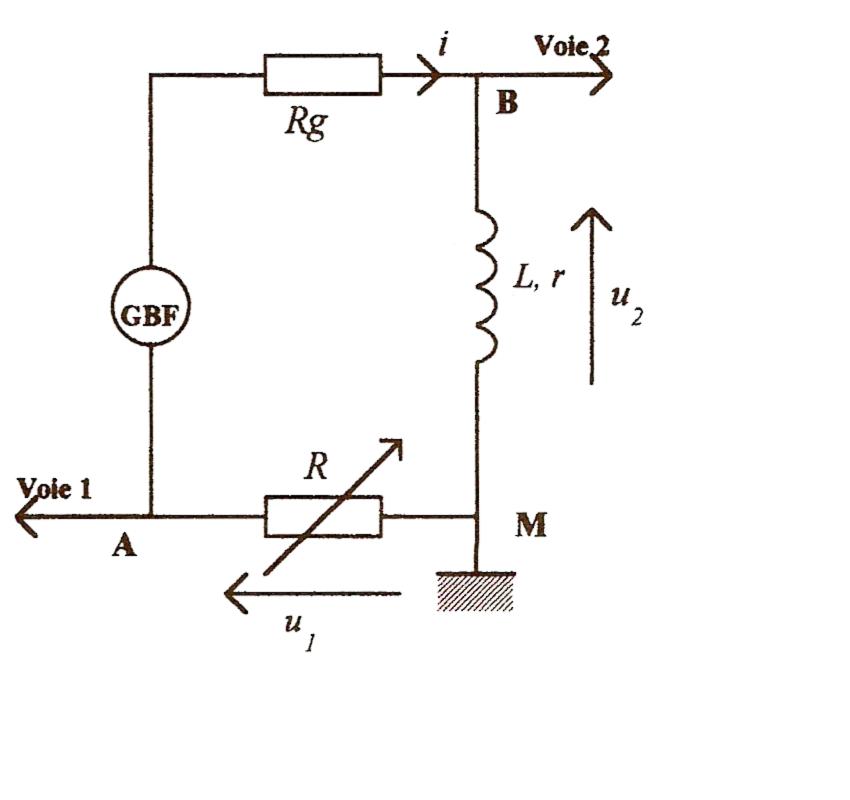
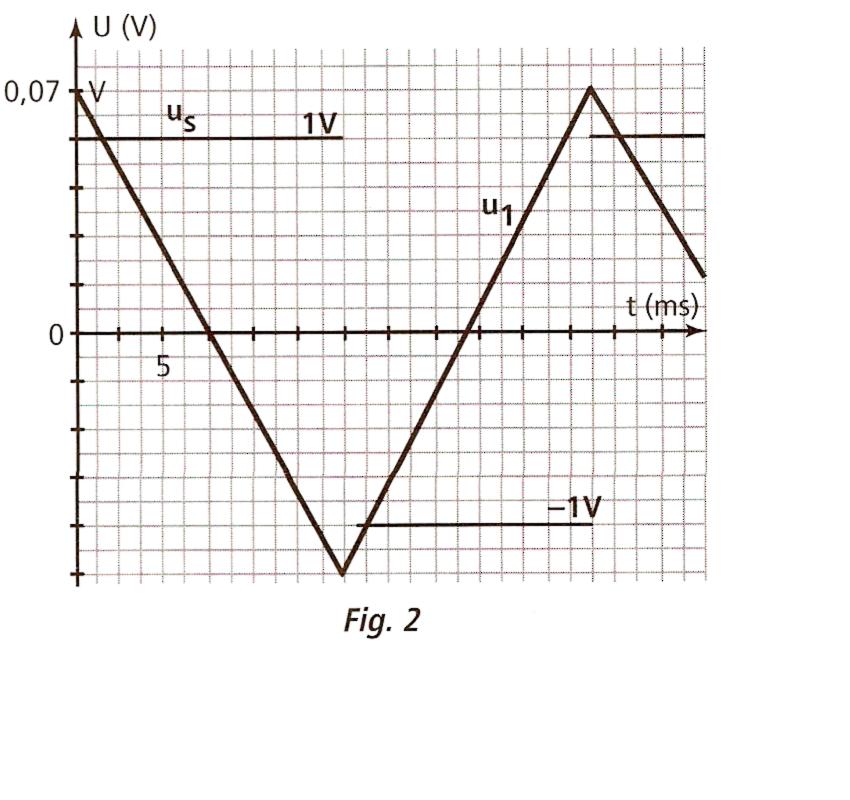
L'oscilloscope est branché comme indiqué sur le schéma. La touche ADD de l'oscilloscope permet d'observer la somme Us= U1 + U2. Sur la figure 2 on a reproduit avec la même origine des temps les courbes U1(t) et US(t).
1) Quel appareil permet de mesurer simplement la résistance r de la bobine.
2) Exprimer en fonction de i(t), r, R et L les tensions suivantes : UAM, UBM, US(t).
3) L'oscillogramme ci-desus a été obtenu en ajustant R à la valeur de r.
a)Montrer que dans ce cas US(t) = - L/R dU1/dt.
b)Déterminer L en exploitant l'oscillogramme.
Partie B
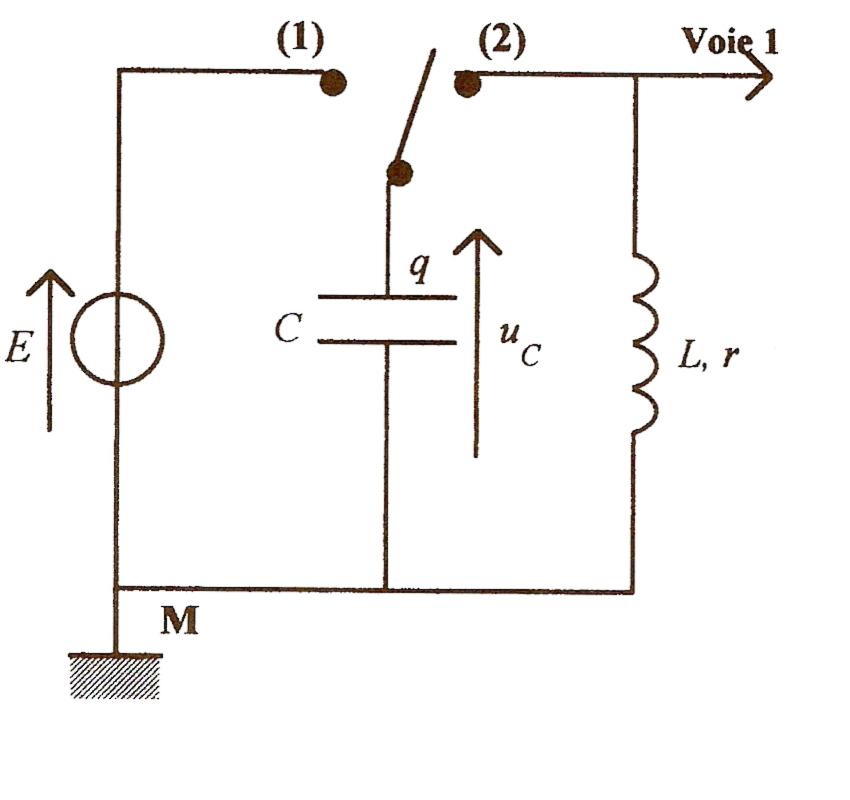
On réalise le montage ci-dessous avec un générateur de tension continue ; le condensateur a une capacité C = 0,55 
F. On utilise l'ordinateur pour enregistrer au cours du temps les variations de la tension UC aux bornes du condensateur. On charge le condensateur puis on bascule l'interrupteur pour obtenir la décharge oscillante.
4) Vérifier que l'expression 2
(LC) est homogène à un temps.
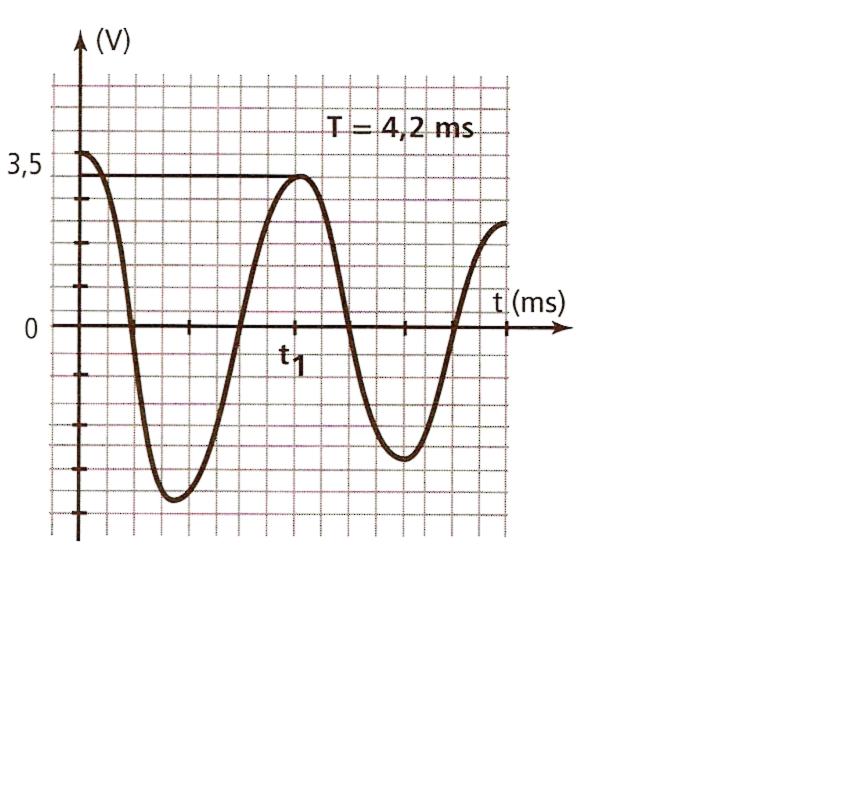
5)la pseudo-période des oscillations est égale à 4,2 ms.
En déduire la valeur de l'inductance L en assimilant la pseudo-période à la périodes des oscillations libres du circuit LC.
6) étude énergétique
a) Exprimer l'énergie emmagasinée dans le condensateur à la date t1=4,2ms. Calculer sa valeur en utilisant le graphique.
b) Expliquer l'origine de l'amortissement des oscillations.
Bonsoir,
2)
UAM(t) = u1 = - R i(t)
UBM(t) = u2 = r i(t) + L di(t)/dt
US(t) = u1 + u2 = - R i(t) + r i(t) + L di(t)/dt
3)
a) Si R = r :
US(t) = - r i(t) + r i(t) + L di(t)/dt
US(t) = L di(t)/dt
u1 = - R i(t) ==> i(t) = -u1 / R ==> di(t)/dt = (-1/R) du1/dt
==> US(t) = (- L/R) du1/dt
b) D'après l'oscillogramme, u1 a un 
u de -0,14 V pour un t de 15 ms ==> du1/dt = -0,14 / 15.10-3
Donc L = - R US(t) / du1/dt
L = 8,0.1.15.10-3/0,14
L = 0,86 H
Voilà pour le A... Pas très difficile
...
US(t) = (- L/R) du1/dt ==> L = - R US(t) / (du1/dt)
u1 est un signal triangulaire composé de segments de droite.
du1/dt est la dérivée de u1. Pour un segment de droite, du1/dt = u1/t = (u11-u10)/(t1-t0).
On prend donc les points extrêmes du 1er segment :
u11 = -0,07 V et t1 = 15 ms
u10 = 0,07 V et t0 = 0 ms
Donc :
u1/t = (u11-u10)/(t1-t0) = (-0,07 - 0,07) / (15.10-3 - 0) = -0,14 / 15.10-3
Sur le même oscillogramme, on a US(t) = 1 V pour 0 
t 15 ms.
Donc il suffit de remplacer dans la formule :
L = - R US(t) / (du1/dt) = 8.1 / (0,14 / 15.10-3) = 8.15.10-3 / 0,14 = 0,86 H
Tu peux faire une analyse dimensionnelle rigoureuse en utilisant les grandeurs de base du système SI (M, L, T, I) ou tu peux faire quelque chose de plus simple...
La dimension de L, c'est .s
La dimension de C, c'est -1 .s
Donc la dimension de est
C'est donc bien homogène à un temps.
E= 3,37.10-6 J ?
6)b) c'est la résistance du dipôle qui est à l'origine de l'amortissement des oscillations ?
E= 3,37.10-6 J ?
Exact.
c'est la résistance du dipôle qui est à l'origine de l'amortissement des oscillations ?
Oui... Dans un circuit RLC, il y a échange d'énergie (magnétique) entre la bobine et le condensateur (énergie électrostatique) en permanence. La résistance dissipe une partie de cette énergie par effet Joule (chaleur). C'est pourquoi l'amplitude des oscillations diminue...
Annuler
connectez vous