Bonjour et bonnes fêtes

1. Influence d'une bobine dans un circuit électrique
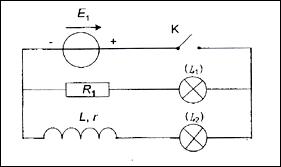
Les élèves réalisent le circuit représenté sur la figure 4. Ce circuit est constitué d'une source de tension idéale de force électromotrice (fem) E1 d'une bobine d'inductance L et de résistance r, d'un conducteur ohmique de résistance R1 de même valeur que r et de deux lampes identiques (L1) et (L2).
Données :
Valeur de la fem : E1 = 24 V.
Valeurs données par le constructeur : L = 1 H ; r = R1 = 7 Ω
Dans cette partie seulement, pour simplifier l'analyse qualitative, on suppose que chaque lampe a le même comportement électrique qu'un conducteur ohmique de résistance RLampe.

1.1. Immédiatement après la fermeture de l'interrupteur K, les deux lampes ne s'allument pas simultanément : une lampe brille quasi-instantanément, l'autre brille avec retard. Quelle lampe s'allume la première ? Pourquoi l'autre lampe s'allume-t-elle avec retard ? L1 s'allume en premier et L2 s'allume avec un retard car la bobine empêche le courant de passer instantanément.
1.2. Dans la branche du circuit contenant la bobine, on peut observer successivement deux régimes différents pour le courant électrique.
Nommer ces deux régimes. Régime transitoire, puis une fois le courant « max » établi : régime permanent.
1.3. Que peut-on dire de la luminosité des deux lampes en fin d'expérience ? Justifier. Comme r=R1 en régime permanent , donc en fin d'expérience, les 2 lampes ont même luminosité. UL= Ldi/dt + ri  or en régime permanent i est maximale et constante donc UL=L* 0 +ri =ri=R1 * i

1.4. On appelle τ la constante de temps caractérisant l'évolution temporelle de l'intensité du courant électrique lors de l'association en série d'un conducteur ohmique de résistance R et d'une bobine d'inductance L. Dans le cas étudié R = R1 + RLampe. La durée nécessaire pour atteindre la luminosité maximale est de l'ordre de 5 τ.
     a)  Exprimer la constante de temps τ en fonction de l'inductance L et de la résistance R.
   τ =L/Rtotale ;             Rtotale = R+ r+Rlampe = R +R1+Rlampe=R+R=2R  donc τ =L/2R

     b)  Vérifier par analyse dimensionnelle, que l'expression obtenue est bien homogène à un temps.  UL=Ldi/dt + ri ??…
    c)  Justifier par un calcul d'ordre de grandeur le fait que ce phénomène est détectable par un observateur. On prendra R ≈10 Ω.
On précise que l'œil est capable de distinguer deux images consécutives séparées d'au moins 0,1 s.

ps: l'image attachée se situe normalement au tout début de l'énoncé
merci de votre aide