Inscription / Connexion Nouveau Sujet
Diagramme de bode
Bonjour à tous.
Meilleurs vœux 2023.
Tous mes vœux de réussite.
Je bute sur un exercice sur le diagramme de bode.
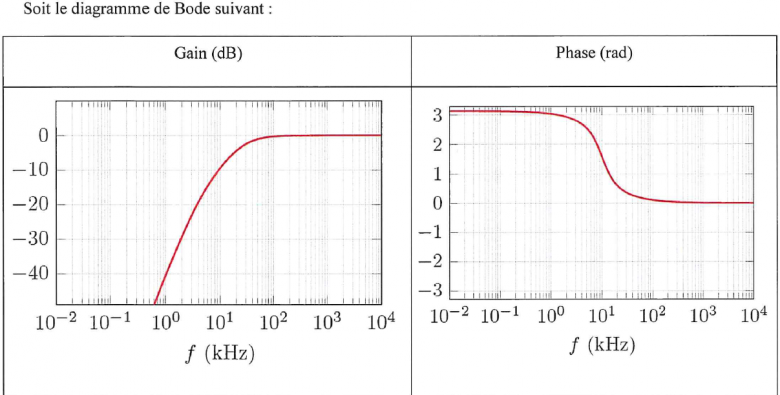
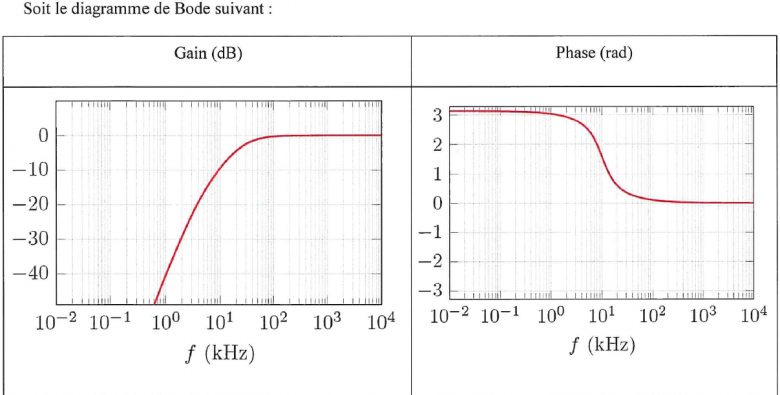
Soit le diagramme de bode suivant (cf pj).
1. Quel est le type du filtre
2. Déterminer graphiquement la fréquence de coupure
3. On applique en entrée de ce filtre le signal.
e(t) = E0 +E0 sin(w. t)
Avec E0= 5V
F= 10kHz
Calculer le signal de sortie de ce filtre.
Bonjour,
Ce que je trouve.
1. C'est un filtre passe haut car il laisse passer les fréquences hautes.
2. Fq de coupure.
Les fréquences vérifiant G(f) = Gmax - 3dB sont appelés fréquences de coupure.
Soit . 0- 3dB =-3dB
Je trouve graphiquement 36500Hz.
3.
Etant donné que Le signal est s'atténue jusqu'à 0 après 36500 Hz.
On peut dire que s(t) =E0.
Qu'en pensez vous ?
Merci.
Bonne journée
Bonjour
Il s'agit bien d'un passe haut. Pour la fréquence de coupure : difficile de vérifier ta valeur car les graduations n'apparaissent pas clairement sur ton document. L'ordre de grandeur me parait cependant correct.
Pour 3 :
1° : action sur Eo : un signal continu peut être considéré comme le cas limite d'un signal de fréquence nulle. Dans ces conditions, qu'elle est l'action du filtre sur ce signal ? Ton résultat proposé est en contradiction avec la notion de passe-haut !
2° : action sur le signal de fréquence 10kHz : quelle est la valeur de G à cette fréquence ? Quelle est la valeur de la phase à cette fréquence ?
Pour t'aider et vérifier tes résultats, voici une simulation du fonctionnement du filtre.
* en rouge : variation de la tension d'entrée en fonction du temps ;
* en bleu : variation de la tension de sortie en fonction du temps.
PDF - 46 Ko
Bonjour Vanoise.
La reprise des études, n'est pas aussi facile que prévu.
D'après le cours. H(j.w)= Us/Ue
Dans ma boîte à outils.
J'ai les graphiques. Mais je ne vois pas comment je peux m'en servir.
La reprise des études, n'est pas aussi facile que prévu.
Je te crois volontiers !
J'ignore ton niveau ; tu as peut-être quelques difficultés à bien te servir des modules et des arguments des complexes. Ce document te sera peut-être utile, en particulier les paragraphes 1.2 à 1.5 :
Tu as un filtre passe- haut. Les très basses fréquences et les signaux continus ne sont pas transmis par le filtre. La tension continue de valeur Eo n'est pas transmise. Reste à étudier l'influence du filtre sur la tension sinusoïdale : v=Eo.sin(
.t). Par définition de la fonction de transfert, la tension de sortie sera :
vs=T.Eo.sin(
.t+
)
où T est le module de la fonction de transfert et
son argument (la phase).
Graphiquement, pour une fréquence de 10kHz, tu peux déterminer
et G. Puisque G=20.log(T), tu déduis la valeur de T de la valeur de G.
PS : selon les auteurs, la fonction de transfert se note H(jw
) ou T(jw). Plutôt que de raisonner sur les pulsations, il est aussi possible de raisonner sur les fréquences comme cela est fait dans ton autre exercice.Vanoise bonsoir,
Avec ton aide j'arrive aux résultat suivant.
V= 1.26 V
Avec T = 10^ - 1/2
Phi= 1.5 rad
G= - 10 dB
w=10.10^3 rad/s
V= 10^-1/2 x 4 x sin (10x10^3x2pi+1.5)= 1.26V
Tu y es presque mais attention à ne pas confondre amplitude et valeur instantanée.
D'accord, aux incertitudes graphiques près, avec tes valeurs :
1,5rad ; G-10dB ; donc :
-10=20.log(T) ; log(T)=-0.5 : T10-0,51/
100,32
L'amplitude de la tension de sortie est ainsi :
Vsm5*0,321,6V
D'où l'expression de la valeur instantanée de la tension de sortie :
vs(t)1,6.sin(2.104
.t+1,5)
Bonsoir,
Comment pouvons nous savoir pour les différents filtres (passebas, passe haut, passe bande, coupe bande) quand les constantes sont gardées pour le signal de sortie ?
Bonsoir,
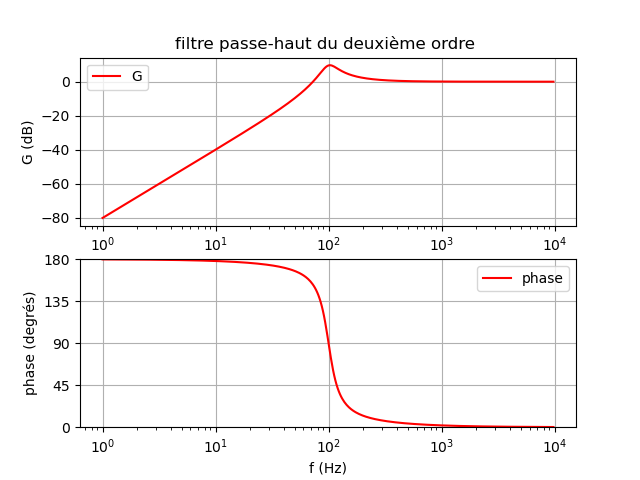
De plus j'ai vu ce type de diagramme. Je n'arrive pas à savoir vraiment son type et ses fréquences de coupures.
N'est pas un filtre passe haut de second ordre ?
Le domaine de fréquence correspondant à l'asymptote horizontale G=0dB renseigne sur la nature du filtre (passe-haut ou passe-bas).
Le diagramme descend trop peu en fréquence pour pouvoir mesurer avec précision la pente de l'asymptote oblique. Tout de même, sachant qu'il s'agit d'un multiple de 20dB/décade, tu vas obtenir l'ordre du filtre. Le résultat serait plus significatif avec le diagramme de la phase...
Enfin, la fréquence de résonance renseigne sur l'ordre de grandeur de la fréquence propre fo du filtre. Enfin l'existence même de cette résonance ainsi que son acuité renseigne sur l'ordre de grandeur du facteur de qualité Q du filtre.
Si je dois porter le regard uniquement sur la pente. Sur l'image, je trouve une pente de-20dB. Je dirais : Filtre passe haut 1er degré
Si on regarde la partie la plus à gauche, donc la plus proche de l'asymptote, on obtient une augmentation de 20dB en sensiblement une demie décade, ce qui correspond à sensiblement 40dB par décade. Donc ?
De toutes les façons, un filtre passe-haut du premier ordre ne présente pas de phénomène de résonance (présence d'un maximum de G plus élevée que la valeur asymptotique : 0dB ici).
Facteur de qualité d'un filtre : cela te parle ?
La somme absolue des pentes est de 60 dB
Où es-tu aller chercher cette histoire de "somme absolue des pentes" ? La pente de l'asymptote oblique est de 40dB/décade dont il s'agit d'un passe-haut du deuxième ordre. Le diagramme des phases aurait fourni plus simplement le résultat : si "n" désigne l'ordre, l'écart entre les deux asymptotes horizontales vaut n.
/2 (en radians).
As-tu compris comment obtenir la fréquence propre fo et le facteur de qualité Q ?
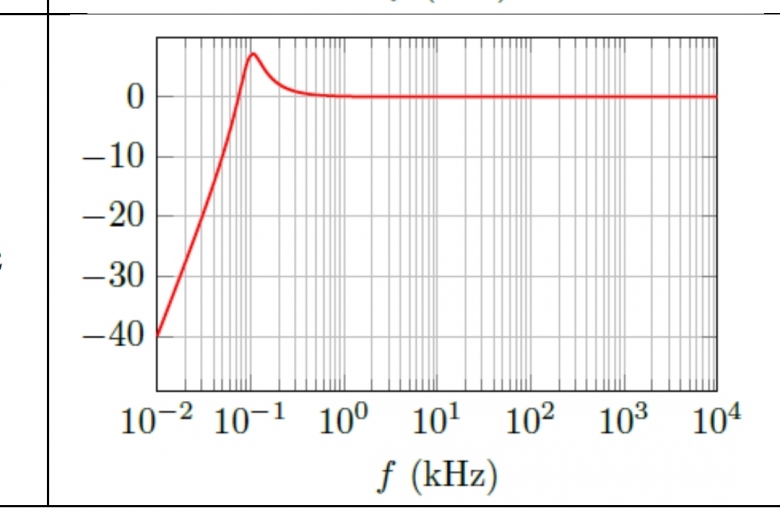
Voici le diagramme qui t'intéresse avec un prolongement des abscisses côté basses fréquences.
Lis bien ton document : la somme des pentes est à prendre en compte pour les passe-bandes et les coupe-bandes par pour les passe-hauts ou passes-bas.
D'autre-part, les pendant à prendre en compte sont celles des asymptotes obliques. Rien à voir avec l'existence ici d'un maximum de gain qui s'explique par un phénomène de résonance.
L'étude générale d'un passe-bas puis d'un passe haut du deuxième ordre est faite ici :
A noter que, quel que soit l'ordre, on passe d'un passe-bas à un passe -haut en remplaçant jx=j/o=j.f/fo par son inverse : 1/(j.x)=-j/x
Annuler
connectez vous
en post-bac