Inscription / Connexion Nouveau Sujet
Dérivée.
Bonjour, simple question
Lors d'une exercice d'élec, on nous donne la densité surfacique 
= dq/dS
L'exercice n'étant pas mon probleme, juste cette relation que je ne comprend pas :
dS = S
Car il me semble que dS = S
et SdS = 1/2 S2
Si quelqu'un pouvait m'éclaircir ..
Merci d'avance.
salut:
il parait que dans l'expression de la surface consédérée il y'a deux varibles.
de quelle surface s'agit il?
Bonjour
C'est une question de math ca !!
Je te conseille de la poster plutot dans le forum de math !!!
La surface est celle d'une sphere, mais dans les calculs suivants, on remplace notre dérivée égale à S par la formule d'une surface ..
J'ai tout l'énoncé sur mon ordi mais lorque que je fais copier coller, ça ne marche pas ....
Bonjour.
La surface est celle d'une sphere, mais dans les calculs suivants, on remplace notre dérivée égale à S par la formule d'une surface
Là d'accord ! Et c'est normal !
Il s'agit simplement dune 'convention' choisie par des mathématiciens et des physiciens.
'dS' (ou parfois dA dans les livres) représente une toute petite surface 'infinitésimale' de ton objet.
D'autres encore notent cela d²S pour rappeler qu'on effectue par la suite une double intégration.
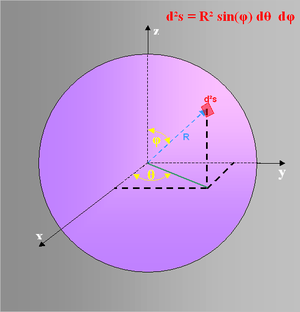
Lorsque l'on ajoute/somme (en maths, on dit 'intègre') tous les petits éléments de surface, tu obtiens la surface totale, notée S (=Surface)
Par 'abus', on écrit
dS = S mais ceci est la même chose que dS = S
S.dS = 1/2 S2Tu as raison SI S est la variable d'intégration...
Il serait plus correct (et plus compréhensible) d'écrire S(x,y).dS qui précise qu'il faut intégrer la fonction S opar rapport à ses deux variables.
Mais vive les raccourcis en physique ! LOL !
Edit Coll : image placée sur le serveur de l'
Merci d'en faire autant la prochaine fois ! 
Oh ... Merci beaucoup pour ta réponse plus que claire !!!
Fichue convention dont on nous parle même pas > <
Un grand merci encore & bonne journée.
( et donc l'intégrale de dS sera toujours égale à S si on considère dS comme infiniment petit ? )
( et donc l'intégrale de dS sera toujours égale à S si on considère dS comme infiniment petit ? )
Oui, c'est la définition même d'une surface... dans la mesure où c'est présenté ainsi !
Maintenant, le soucis est de bien identifier si l'on souhaite intégrer une variable S ou une fonction S(x1, x2; x3, ...).
Deux conseils :
- Je pense qu'il ne faut pas hésiter à demander à votre professeur en fin de cours de lever ce doute, vous permettant ainsi de poursuivre.
- Si vous voulez être quasiment sûr de ne pas vous tromper dans l'intégration, écrivez la fonction ET ses arguments f(x1, x2; x3, ...) même si cela 'alourdit' l'écriture. Vous y perdrez peut-être en lisibilité mais cela ne nuira plus à votre raisonnement.
Annuler
connectez vous