Bonsoir à tous
J'ai un exercice merci beaucoup d'avance
Le thorium ²³⁰_....Th est utilisé dans la datation des coraux et concrétions carbonatées ainsi que dans la datation des
sédiments marins et lacustres.
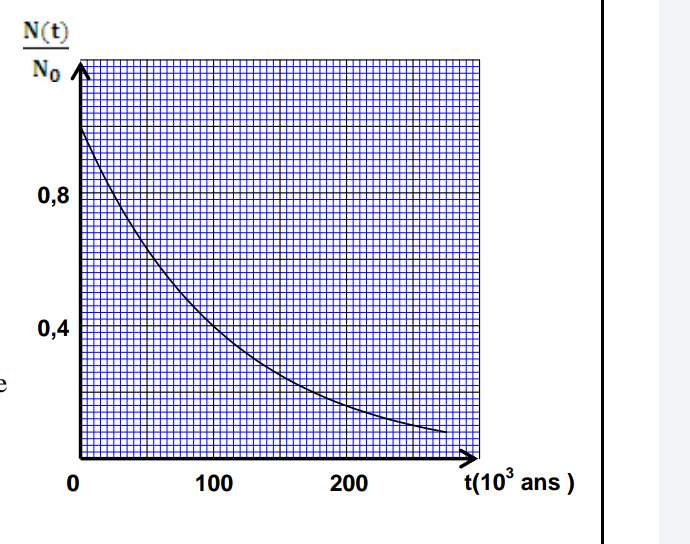
Dans un échantillon de « thorium 230 », on appelle N(t) le nombre de noyaux de thorium présents à chaque date t
et N0 celui des noyaux présents à la date t0 = 0. La courbe ci-jointe représente les variations du rapport en fonction de temps
1.1. Le noyau ²³⁰Th est un émetteur α et se désintègre pour donner du ₈₈Ra. Indiquer ce que représente α et écrire
l'équation de la réaction nucléaire correspondante, en précisant les lois utilisées (le noyau de radium est obtenu
dans un état non excité)
1.2. Déterminer graphiquement le temps de demi vie t1/2 en expliquant succinctement la méthode utilisée.
1.3. Parmi ces grandeurs :
- l'âge de l'échantillon de noyaux
- la quantité initiale de noyaux.
- la température
- la nature des noyaux
Quelle est la seule grandeur qui fait varier le temps de demi-vie ?
2-1) Déterminer graphiquement la constante de temps (en années ) . Puis déduire la valeur de la constante radioactive en an^-1
2-2) Déterminer l'expression de la loi de Décroissance radioactive
2-3) calculer , à partir de la demi-vie t1/2  , la constante radioactive en an^-1
2.4). Le thorium ²³⁰Th fait partie de la famille radioactive de l'uranium ²³⁸U.
Une famille radioactive est composée d'un ensemble de noyaux radioactifs, tous issus d'un noyau initial instable
qui, de père en fils, par désintégrations successives conduisent à un noyau stable, ici le « plomb 206 ».
L' « uranium 238 », dissous à l'état de traces dans l'eau de mer, produit des atomes de « thorium 230 » suivant les
réactions nucléaires suivantes :
₉₂²³⁸ U-->₉₀²³⁴ Th->²³⁴₉₁ Pa =>²³⁴_Z4 U=>²³⁰_Z5 Th
Donner les valeurs de Z₄ et Z₅ , en les justifiants , et indiquer le type de radioactivité pour les deux premières transformations
3). Au début de leur formation, les concrétions carbonatées des coraux contiennent de l' « uranium 238 » et pas
de « thorium 230 ». La méthode de datation de ces carbonates repose sur le rapport des nombres de noyaux :
N(²³⁰ Th )/N(²³⁸ U)
. Ce rapport augmente au cours du temps jusqu'à « l'équilibre séculaire ». Celui-ci correspond à l'état où
les deux populations des noyaux d' « uranium 238 » et de « thorium 230 » ont même activité.
3-1. L'activité A(t) d'une population de noyaux identiques est définie ici par :
a(t)=-dN(t)/d t
Montrer que A(t) = λ.N(t) pour une population de noyaux donnée.
3-2). En déduire, qu'à l'équilibre séculaire : a(²³⁰ Th) =a(²³⁸ U), le rapport
N(²³⁸Th)/N(²³⁸ U) est constant
4) La courbe ci - jointe est utilisée pour dater un échantillon d'un sédiment marin de forme
cylindrique d'hauteur h prélevé dans le plancher océanique.Les résultats d'analyse d'une masse m prélevé dans la base supérieure de cet échantillon montre
qu'il contient ms = 20µg de thorium , par contre la même masse m prélevé dans la partie inférieure
du même échantillon montre qu'il contient uniquement mp =1,2µg de thorium.
Nous considérons qu'à t = 0, m0 = ms
, Calculer l'âge de la partie prélevé dans la base inférieure de l'échantillon, en ans

Mes réponses
D'après les lois de Soddy
₉₀²³⁰ Th=> ²²⁶₈₈ Ra +₂⁴ He ( radioactivité )
La radioactivité est une désintégration nucléaire spontanée naturelle correspond aux noyaux lourds (A
>200)
1-2) on sait que N(t)=N₀ *e^{- t}
<=>
Donc

Une petite indications s'il vous plaît merci beaucoup d'avance
1-3) le temps de demi vie ne dépend que de la nature du noyau
2-1 ) est l'intersection avec l'axe des abscisses
Une petite indications s'il vous plaît merci beaucoup d'avance
2-2) N(t)=N₀* e^-t
N(t) nombre de noyau radioactive à t (restant )
N₀ nombre de noyau radioactive à t=0
constante de la désintégration en s^-1
Merci beaucoup d'avance