Inscription / Connexion Nouveau Sujet
Courbe sinusoïdale explications
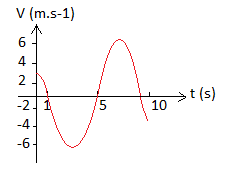
Bonjour, voici un graphique (cf plus bas)
Ici oméga= w
On me demande d'établir l'expression de v(t)
La correction m'indique ceci : v(t)= v(max).cos(w.t+phi)
Je voulais savoir si :
-Toutes les courbes d'aspect sinusoïdal ont toutes le même aspect et donc le même « squelette » d'expression v(t) ?
-le fait de mettre « cos » et non « sin » est il due au fait que l'origine de la courbe ne commence pas à 0 ?
Bonjour,
Oui, les courbes représentant la fonction sinus ou la fonction cosinus ont toujours même aspect.
Sinus ou cosinus : c'est la même courbe (avec un décalage de  /2 rad puisque sin(
/2 rad puisque sin( +
+  /2) = cos(
/2) = cos( ) )
) )
Le fait qu'à l'origine la valeur de la fonction ne soit pas nulle est due, dans le cas de ta figure, à la valeur de  , la phase à l'origine.
, la phase à l'origine.

Ok.
On me demande d'en déduire les expressions de x(t) et a(t) sachant que x(t=0)= 6,6 m
v(t)= v(max).cos(w.t+phi)
a(t)= d(v)/d(t)
donc a(t)= v(max).w.sin(w.t+phi)
Pour trouvez la pulsation: w=(2 )/T
)/T
d'après le graphique, T=8s donc w= /4
/4
On peut déterminer  en prenant v(t=0)=3=6 cos
en prenant v(t=0)=3=6 cos et
et  =60
=60
Tout est bon jusqu'ici?
Maintenant pour trouver x(t), je dois trouver la primitive de v(t)
v(t)= v(max).cos(w.t+ )
)
x(t)= -v(max).sin(w.t+ )
)
Je dois ajouter +6.6 à cette équation car a t=0, x(0)= 6,6 m
ce qui donne:
x(t)= -v(max).sin(w.t+ )+6 ce qui me semble très hazardeux
)+6 ce qui me semble très hazardeux
Pouvez vous m'indiquer la façon de "primitiver" v(t)?
Tu ferais mieux de donner un énoncé complet.
Le dessin du 1er message et le texte du message du 27-08-13 à 15:04 ne s'accordent pas.

Pourtant le dessin est bien rattaché à ce texte dans le livre...
Pour plus de lisibilité je réécrit tout l'énoncé:
La vitesse v(t) d'un mobile en mouvement rectiligne est représentée par la courbe ci dessus (cf 1er message)
1) Établir l'expression v(t) (fais plus haut)
2) En déduire celles de x(t) et a(t) en sachant que x(t=0)= 6,6 m
je ne comprends pas vraiment ton message jp...
ca ne colle pas.
v(t)= v(max).cos(w.t+phi)
Sur le dessin : Vmax = 6
T = 8s ---> w = 2Pi/8 = Pi/4 rad/s
v(t)= 6.cos((Pi/4).t+phi)
Mais on voit que v(1) = 0 ---> 6.cos((Pi/4) + phi) = 0
cos(Pi/4 + Phi) = 0
Pi/4 + Phi = +/- Pi/2
Phi = Pi/4 ou -3Pi/4
dv/dt = -v(max).sin(w.t+phi)
dv/dt = -6.sin((Pi/4).t+phi)
(dv/dt)(0) = -6.sin(phi)
Et le dessin montre qu'en t = 0, on doit avoir dv/dt négatif (puisque v est décroissante).
Et -6.sin(Pi/4) < 0 et -6.sin(-3Pi/4) > 0 et donc Phi = Pi/4
v(t) = 6.cos((Pi/4).t + Pi/4)
Et déjà là, cela foire, car on peut calculer V(0) = 6*cos(Pi/4) = 4,24 ... alors que le graphe montre V(0) = 3
-----
Le dessin suffit à lui-même pour établir que v(t) = 6.cos((Pi/4).t + Pi/4) mais il y a visiblement une bisbrouille en t = 0
On peut alors calculer a(t) ; dérivant v(t)
a(t) = - 6*(Pi/4).sin((Pi/4).t + Pi/4)
a(t) = - (3Pi/2).sin((Pi/4).t + Pi/4)
On a aussi :
v = dx/dt = 6.cos((Pi/4).t + Pi/4)
dx = 6.cos((Pi/4).t + Pi/4) dt
x = (6*4/Pi).sin((Pi/4).t + Pi/4) + K
x(0) = 6,6
6,6 = (6*4/Pi).sin(Pi/4) + K
K = 6,6 - 24/(V2.Pi)
K = 6,6 - 12.V2/Pi
x(t) = (24/Pi).sin((Pi/4).t + Pi/4) + 6,6 - 12.V2/Pi
-----
Mais tout ceci à partir de la courbe donnée pour v(t) qui a manisfestement une bisbrouille comme mentionné.
Sauf distraction. 


