Inscription / Connexion Nouveau Sujet
Contraction due à la vitesse en relativité
Bonjour. Dans F. Selleri, WEAK RELATIVITY the physics of space and time without paradoxes (en ligne sur http://blog.hasslberger.com/docs/Selleri_Weak_Relativity.pdf ), on lit ceci : "Two inertial reference systems are given, S0 of the stationmaster and S of the passenger on the train. Let v =0,6c be the train velocity, hence the Lorentz factor is (...) 0.8. It follows in the standard way that if the stationmaster sees a meter immobile in the train parallel to the rail and measures its length, he finds 80 cm. Similarly, if the passenger on the train sees a meter immobile in the railway station parallel to the rail, and measures its length he finds 80 cm. 'My meter is longer than
yours' will say the stationmaster, and the same words will be repeated by the passenger."
Supposons que le train roule du sud au nord et que les deux mètres sont dans cette même direction. Quand les extrémités sud des deux mètres sont à la même hauteur, et seulement à ce moment, on met les deux mètres en contact, de façon à ce que les extrémités sud se touchent. D'après le passage que j'ai cité plus haut, le voyageur voit ceci : l'extrémité nord du mètre du chef de gare touche le mètre du voyageur, mais elle ne touche pas l'extrémité nord du mètre du voyageur, elle touche un autre point du mètre. Et le chef de gare voit ceci : l'extrémité nord du mètre du chef de gare ne touche pas le mètre du voyageur.
Est-il possible qu'il y ait contact pour un observateur et pas pour l'autre ? Merci d'avance pour toute réponse.
Rrelativo
Edit Coll : forum et niveau modifiés ; merci de poster à l'avenir dans ton niveau
Bonjour,
Tu as bien compris que tout se joue sur la simultanéité ; et ce qui est simultané pour un observateur (permettant la mesure d'une longueur) ne l'est pas pour l'autre observateur.
Si t = 0 s dans les deux référentiels est l'instant où les deux "extrémités sud" sont l'une en face de l'autre et donc où les deux observateurs font la mesure des longueurs
Le chef de gare voit "l'extémité nord" du mètre du train là où elle était à un instant < 0 s dans le référentiel du train.
Le passager du train voit "l'extrémité nord" du mètre du quai là où elle sera à un instant > 0 s dans le référentiel du quai.
Pour le passager du train la coïncidence des "extrémités nord" a lieu pour t < 0 s (temps du référentiel du train)
Pour le chef de gare, la coïncidence de ces "extrémités nord" a lieu pour t > 0 s (temps du référentiel de la gare)

Je ne pense pas que les diagrammes de Minkowski soient à ton programme. Je poste malgré tout celui qui m'a permis de te répondre.
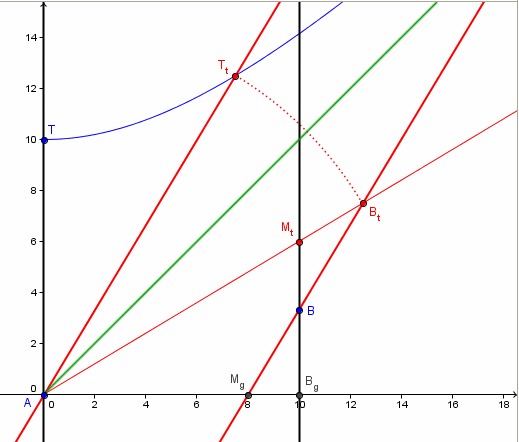
Le référentiel noir est celui de la gare (origine : A ; axes des longueurs ABg et des temps AT)
Le référentiel rouge est celui du train (origine : A ; axes des longueurs ABt et des temps ATt)
Les graduations et les unités en noir sont celles de la gare (abscisse : longueur ; ordonnée : temps)
La durée AT est la même que la durée ATt
La longueur ABg est la même que la longueur ABt : elle vaut 1 mètre dans les deux cas
Les deux lignes noires verticales (AT et BgMt) sont les lignes d'univers des extrémités du mètre de la gare
Les deux lignes rouges inclinées (ATt et MgBt) sont les lignes d'univers des extrémités du mètre du train
A est l'évènement : les deux extrémités A des deux mètres sont confondues (au même emplacement au même instant)
B est l'évènement : les deux extrémités B des deux mètres sont confondues
Le chef de gare mesure le mètre du train et lui trouve une longueur AMg = 0,8  ABg = 80 cm
ABg = 80 cm
Le passager du train mesure le mètre de la gare et lui trouve une longeur AMt = 0,8  ABt = 80 cm
ABt = 80 cm
Bonne réflexion !

Merci pour la réponse et le graphique soigné. J'aimerais dire tout de suite que j'ai compris, mais je vais devoir trouver le temps de réfléchir.
Relativo


