Inscription / Connexion Nouveau Sujet
circuit RLC
bjr à tous j'ai besoin d'aide à propos de ce sujet aidez moi svp.
on considère le dipole AC associant en serie un conducteur ohmique de reistance R=20ohm avec une bobine de resistance r et d'inductance L inconnues
Ce dipole est alimenté par un generateur de tension sinusoïdale u=90racine(2)cos(100pi)t.
A l'aide d'un volmetre on mesure les tensions efficace U1(tension du conducteur ohmique) U2 (tension de la bobine )telles que U1=50V et U2=50V
1-a) representer le diagramme de fresnel des tensions U1,U2 et U(ac) y faire apparaitre la phase (fi) de la tension U2 aux bornes de la bobine par rapport à l'intensité du courant
echelle: 1cm pour 50V
1-b)Determiner graphiquement cos(fi)
1-c)A partir d'une construction de fresnel exprimer la tension U(ac) aux bornes du dipole AC en fonction de U1, U2 et cos (fi)
j'ai répondu aux 2 premiere questions mais la derniere je ne vois pas comment repondre
au 1-b) j'ai trouvé (fi)=23pi/90
Bonjour,
Je ne trouve pas le même résultat que toi pour la question 1-b)
Question 1-c) : Applique le théorème d'Al-Kashi
Impossible !
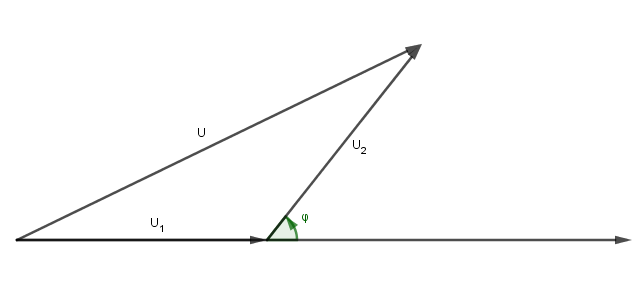
Regarde la figure.
L'angle φ ( déphasage de U2 par rapport à l'intensité du courant ) a une valeur comprise entre 0 et π/2
Donc cos(φ) est compris entre 0 et 1 et ne peut pas avoir une valeur négative comme tu l'as trouvée.
mais j'ai une question pourquoi lorsque je fais l'application numerique ça donne moin est ce que je dois mettre le cos(fi) en valeur absolu
cos(fi)=[ U1(carré)+U2(carré)-U(carré)]/2*U1*U2
c'est cette operation qui me donne cos(fi) negatif
La formule que tu utilises pour calculer U² est-elle bien U² = (U1 + U2)² = U1² + 2*U1*U2*cos + U2² ?
+ U2² ?
mais j'ai une question pourquoi lorsque je fais l'application numerique ça donne moin est ce que je dois mettre le cos(fi) en valeur absolu
cos(fi)=[ U1(carré)+U2(carré)-U(carré)]/2*U1*U2
c'est cette operation qui me donne cos(fi) negatif
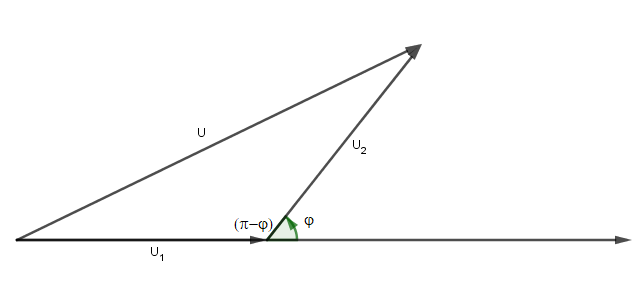
La relation que tu utilises est "presque" correcte, mais elle calcule non pas cos(φ) , mais le cosinus de l'angle qui est opposé au vecteur
La relation exacte est donc :
L'application numérique donne : cos (π-φ) = - 0,62
Or comme la question porte sur cos(φ) et non sur cos (π-φ) on utilise la relation trigonométrique :
cos(φ) = - cos (π-φ)
On obtient donc finalement : cos (φ) = 0,62