Inscription / Connexion Nouveau Sujet
Circuit R // LC
Bonjour,
J'ai eu mon bac STI Electronique il y a 20 ans. Pour mon travail je dois faire une préparation niveau bac+2 qui me plonge dans les maths et la physique. J'ai un sujet de physique sur lequel je bloque un peu.
Données U=230 V ; f=50Hz ; R=200ohm ; L=0.4H ; C=10OµF
1/Calculer Z_R et Z_LC (je mets les traits à coté et non en dessous car je n'y arrive pas)
Z_R = R = 200 ohm
Z_LC = jLw + 1/jCw=j(Lw-1/Cw)=93.83j
2/Calculer les courant I_1 et I_2, en déduire les valeurs efficaces
forme trigo de Z_R =[200:0] , Z_LC=[93.83;0] et U_=[230;0]
U_=Z_R*I_1 et U_=Z_LC*I_2
I_1=U_/Z_R=|rhoU/rhoR; thétaU-thétaR]=|1.15;0]
I_2=[2.45;0]
Ieff1=1.15A et Ieff2=2.45A
3/Calculer U_L et U_R, en déduire les valeurs efficaces
U_L=Z_L*I_2 et U_C=Z_C*I_2
Z_L=[125.66;pi/2] et Z_C=[31.83;-pi/2]
U_L=[307.87;pi/2] et U_C=|78;-pi/2]
UL=307.87V UC=-78V
4/Calculez Z_tot
A partir de cette partie je commence à avoir des gros doutes sur mes résultats
Ytot=1/R + 1/j(Lw-1/Cw)=1/R -j/(Lw-1/Cw)
Module de Y =Racine((1/R)²+(-1/(Lw-1/CW))²)=0.01177
Ztot=1/Ytot=85V
thétatot=86.19
5/Calculez I_e
I_e=I_1+I_2=[3.6;0]
Je pense avoir faux ici ou la question d'avant
car U=Ztot*Ie et avec mes résultats je ne retrouve pas [230;0]
J'aimerais valider ou non mes premiers résultats.
Merci d'avance pour vos réponses
Raz29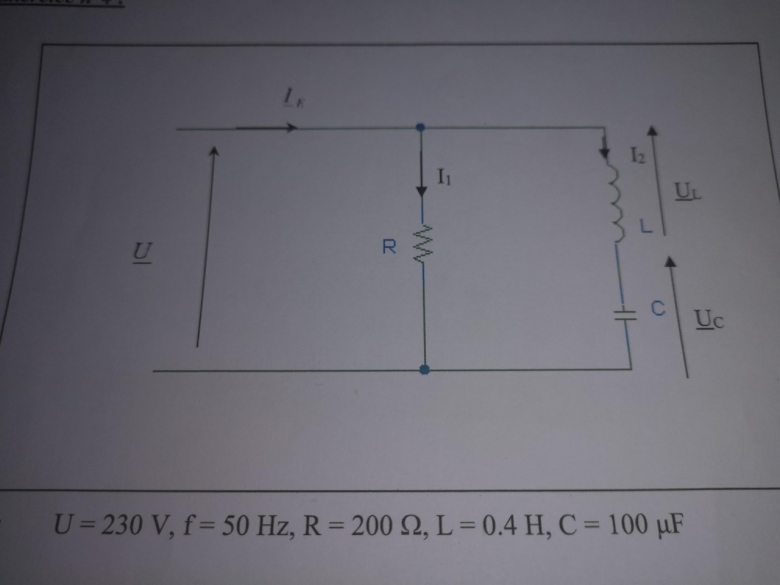
***Niveau profil mis en accord avec le sujet (reprise études)***
Pas de problème pour les premières questions .
Tu obtiens ensuite UL<0 : impossible pour une valeur efficace.
Attention aux unités également.
Merci Vanoise pour ces réponses rapides.
Juste deux précisions :
Quand vous me dites que Ul<0 impossible pour une valeur efficace dois-je conclure que ma réponse UL=[307.87;pi/2] est fausse ?
De plus, je ne vois pas qu'elles sont mes unités de fausse ?
Cordialement
Tu oublis parfois les unités ; celles que tu utilises sont correctes. Je voulais juste dire qu'une valeur efficace de tension ne peut en aucun cas être négative mais je me suis trompé d'indice : c'est Uc que tu as trouvée négative.
Je viens de reprendre pas à pas tes calculs. Tout va bien jusqu'à la détermination de l'intensité dans la branche LC. La valeur efficace est bien Ieff2=2,45A mais la phase initiale de cette intensité n'est pas nulle dans la mesure où l'argument de ZLC n'est pas nul. Cela amène à revoir une partie des résultats qui suivent.
N'oublie pas de vérifier que l'on obtient bien :
UL+UC=U
Bon, même avec toute ton aide je n'arrive pas à trouver ou je me trompe
Z=a+jb
Module de Z=Racine(a²+b²)
Argument de Z=Arctan(b/a)
Pour ZLC
Module de ZLC=93.83ohm
Argument de ZLc= ArcTan(93.83/0) hors une division par zéro est impossible
Du coup, je ne vois pas comment trouver que l'argument de LC est non nul.
Pour U_=U_L+U_C, je me suis mal exprimé.
Mes résultats ne sont pas la valeur efficace mais la forme algébrique.
Dans tout les cas les valeurs sont fausse car avec UL=307.87j et UC=-78j ça donne
U_=230j au lieur de U_=230
Je sais que le but de ce forum n'est pas de donner les réponses mais je ne vois pas comment avancer dans mon problème.
Cordialement
Z=a+jb
Module de Z=Racine(a²+b²)
Argument de Z=Arctan(b/a)
Oui pour le module. Oui aussi pour l'argument mais seulement à condition que : a>0 mais c'est le cas pour les circuits faisant intervenir R, L et C.
Dans les cas simples comme ici, il est préférable de juste partir de l'expression de l'impédance complexe.
Premier cas :
Deuxième cas :
Tu es ici dans le premier cas.
D'accord avec toi pour UL et UC.
Merci pour l'info.
Je vais refaire les calculs pas par pas.
1/Calcul de Z_R et Z_LC
ZR=R=200
forme algébrique ZR=200.0j
forme trigo : ZR=[200;0]
ZLC=j(LW-1/CW)=93.83j
forme algébrique ZLC=0+93.83j
forme trigo ZLC=|93.83; ]
]
J'avais oublié de préciser une remarque importante du devoir:
Une fois que vous aurez donné les expression littérales des différentes grandeurs demandées, passez immédiatement aux calculs. Vous ferez vos calculs en utilisant les valeurs efficaces.
2/Calcul de I1 et I2, plus Ieff1 et Ieff2
Du coup pour U si je prend la valeur efficace ça me donne
U=[162.63;0]
I1=U/ZR=[162.63/200;0-0]=[0.81;0]
forme trigo I1=[0.81;0]
forme algébrique I1=0.81+0j
Ieff=|I1|=0.81A
I1=U/ZLC=[162.63/93.83;0- =[1.73;-
=[1.73;- ]
]
forme trigo I1=[1.73;- ]
]
forme algébrique I1=-1.73+0j
Ieff=|I1|=1.73A
Correction poste précédant
I2=U/ZLC=[162.63/93.83;0- ]
]
forme trigo I2=[1.73;- ]
]
forme algébrique I2=-1.73+0j
Ieff2=|I2|=1.73A
J'ai laissé passer une erreur tout à l'heure :
module( ZLC) : 93,83 ; argument( ZLC) : 90° et non 180° (
; argument( ZLC) : 90° et non 180° ( /2 rad si tu préfères)
/2 rad si tu préfères)
U=230V représente la valeur efficace de la tension d'alimentation et non la tension maximale, souvent noté Um ou Umax. C'est la tension efficace nominale en France pour le réseau EDF monophasé.
Les valeurs efficaces de I1 et I2 que tu avais obtenues précédemment étaient donc correctes. Je récapitule :
Pour I1 : valeur efficace : 1,15A ; phase initiale : 0°
Pour I2 : valeur efficace : 2,45A ; phase initiale : -90°
Ok grâce à toi j'ai bien pu avancer.
2/Calcul de UL et UC
I2=[2.45;- /2] ; ZL=[125.66;
/2] ; ZL=[125.66; /2] et
/2] et
ZC=[31.83;- /2]
/2]
UL=ZL*I2=[308;0]=308+0j
UC=ZC-I2=[78;- ]=-78+0j
]=-78+0j
U=UL+UC=308-78=230 c'est cohérent
3/Calcul de Ztot
Ztot=(ZR*ZLC)*(ZR+ZLC]=[85;65°]
4/Calcul de Ie
Ie=I1+I2=[2.70;-65°]
Pour vérifier je peux calculer U=Ztot*Ie=[230;0]
c'est encore une fois cohérent
4/Calculer P, Q, S et cos( )
)
P=U*Ie*cos(65°)=262.44W
Q=U*Ie*sin(65°)=562.81W
S= P²+Q²=620W
P²+Q²=620W
cos( )=P/S=0.42
)=P/S=0.42
5/Donner le déphasage total
 tot=
tot= u-
u- i=65°
i=65°
6/ l'installation est-elle globalement inductive ou capacitive ?
je dirais inductive car UL>UC
D'accord avec toi. Un peu plus simple pour la puissance apparente : S=U.Ie.
Pour bien distinguer ces différentes puissances, bien qu'elles aient toutes les trois la dimension physique d'une puissance, il est d'usage d'exprimer P en watts, Q en VAr (voltampères réactifs) et S en V.A (voltampères)



 en post-bac
en post-bac