Bonjour,

Il faudrait le sujet complet : avec les données fournies, il est impossible de répondre.

Énoncé Complet
Un générateur de courant alternatif maintient entre deux bornes A et B une différence de potentiel sinusoïdale de valeur maximale U_m = 282,8 V et la fréquence f=60 Hz .
On branche en série entre les bornes de A et B , un condensateur de capacité C= 13,25F et une bobine dont la résistance est R= 15 ( et donc l'inductance L peut être choisie à volonté entre 0,1 et 1 H ) .
Questions
1) Valeur efficace de U

2) En utilisant la construction de Fresnel , établir la relation entre U et l'intensité efficace I  dans le circuit lorsque l'inductance est L .

3) La Bobine est réglée de telle sorte que L= 0,797 H , déterminer :

a) les tensions efficaces U₁ et U₂ aux bornes de la Bobine et du condensateur respectivement .

b) les énergies W₁ et W₂ dissipées en 10 min sous forme de chaleur dans la Bobine et dans le condensateur .

c) Facteur de puissance

4 ) Quelle doit être la valeur L₀ de L pour que le circuit se comporte comme une résistance pure ? Cette condition étant réalisée Calculer :

a) l'intensité efficace I' du courant et les tensions efficaces U₁' et U₂' aux bornes de la Bobine et du condensateur .

b) Calculer l'énergie dissipée en 10 min dans le circuit ainsi réglé . De combien cette énergie pourrait elle élever la température de 5 L d'eau ?

Ce = 4,18 kJ/Kg /K

Bonjour,

Pour 3b, dans quel composant dissipe-t-on de la puissance et quelle est la puissance correspondante ? Ensuite utiliser la relation énergie puissance.

Pour
3b ) La puissance est dissipée dans la résistance R ( Puissance dissipée par effet joule )
Et l'énergie correspondante est :
W= P.t = R.I².t

Mon soucis c'est lorsqu'on demande W₁ et W₂.... Parceque normalement aucun des composants ( Bobine et condensateur ) ne restituent pas l'énergie stockée . Ou bien je me trompe ?!

En régime sinusoïdal, en moyenne, le travail est en effet nul pour une capacité et une inductance, mais j'ai bien dit capacité et inductance et non condensateur et bobine.

Donc votre réponse de 14:14 est la bonne. La résistance R est la résistance de la bobine.

Ok donc si je comprends bien :
W₁=W₂=W C'est celà ?

Non : W1=W (résistance de la bobine) ; W2=0 (condensateur)

Ok merci à vous gts2 .

C'est encore moi , Besoin d'une piste pour la question 4) Svp
Merci d'avance

Bonsoir,

Pour une résistance pure, U=RI, comment cela se traduit-il sur votre diagramme de Fresnel de la question 2 ?

Pour une résistance u et i sont en phase... Je comprends pas bien ce que vous me poser comme question

Je peux facilement faire la représentation de Fresnel . Mais je comprends pas vraiment ce que vous demandez

Pour une résistance pure U= RI ainsi pour que le circuit se comporte comme une résistance Pure il faudrait que l'impédance Z de ce circuit soit égale à R cela implique que =0 donc L_oCW²=1 donc
avec W= 2πf .
Cela peut être considéré comme correct aussi ?

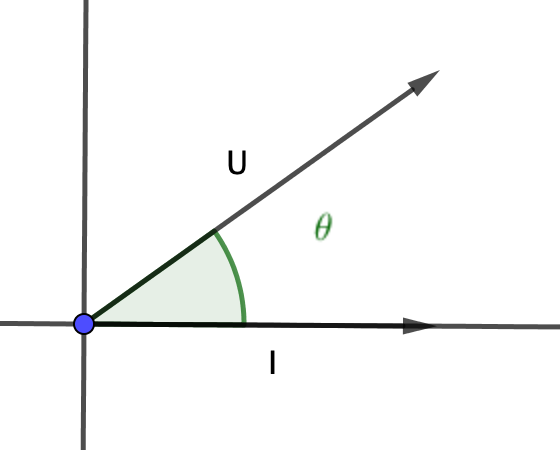
Dans un diagramme de Fresnel, la phase entre U et I apparait ainsi.
Comment choisir L dans votre diagramme de la question 2 pour avoir =0 ?

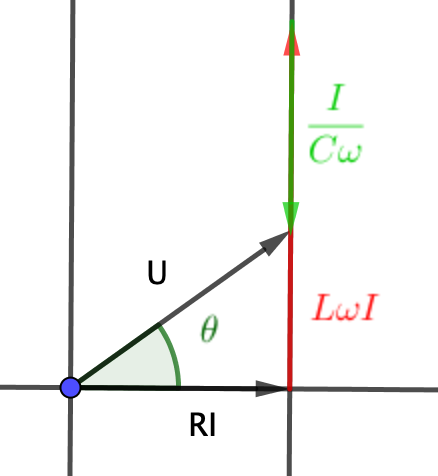
L intervient dans l'expression de l'impédance Z pour que =0 il faut que Z=R c'est-à-dire... Comme fait dans cette réponse

Vardy @ 18-08-2020 à 07:55

Pour une résistance pure U= RI ainsi pour que le circuit se comporte comme une résistance Pure il faudrait que l'impédance Z de ce circuit soit égale à R cela implique que =0 donc L_oCW²=1 donc
avec W= 2πf .
Cela peut être considéré comme correct aussi ?

Oui, c'est bien cela, je m'appuyais sur un graphe plutôt que sur une forme analytique au vu du sujet qui ne calcule nulle part Z mais qui trace un diagramme de Fresnel qui doit ressembler à cela. Comment rendre nul ?

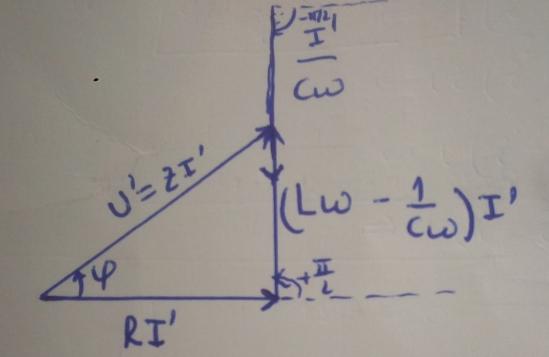
Pour rendre = 0 il faut que U=RI bref les vecteurs qui représentent U et RI soient colinéaires de même sens .

Il faut aller jusqu'au bout : ce qui donne bien .

Oui vous avez raison.  Merci à vous

Ainsi après avoir Calculer L_o pour 4) on a
a) •
      
      • U'₁ = L_oI'
      • U'₂ = I'/C'
Est-ce cela ? Merci

OK pour U'2
Pour U'1, toujours le même problème : une bobine n'est pas une inductance, elle est ici modélisée par une résistance et une inductance en série.

Ok c'est vrai vous avez raison , merci ainsi U'₁ = RI' + L_oI'

Non, retour une nouvelle fois au diagramme de Fresnel, représenter les deux tensions (résistance et inductance) et "lire" sur le schéma la somme des deux.

Voici le diagramme de Fresnel représenté .

J'ai trouvé ceci au final :
V₁ représente U'₂
V₁ représente RI'
V₂ représente LI'
V² =V²₁+V²₂
c'est-à-dire U'₂ =

C'est bien cela.

D'accord . Merci gts2 , J'ai compris encore beaucoup de choses aujourd'hui .

Pour la dernière question :
4b ) L'énergie W dissipée dans le circuit ainsi réglé est :
W=R.I'². t
Et la toute dernière j'y parviens pas

4b) OK

Connaissez-vous la notion de capacité thermique massique de l'eau : énergie nécessaire pour élever un kg d'eau de 1°C ?

Soit :
C la capacité calorifique de l'eau
C_m la capacité calorifique massique
C_M la capacité calorifique molaire . Je sais Juste que :
m.C_m =M.C_M=C . C'est juste cela

Oui c'est bien cela dont je veux parler : il faut donc calculer le C pour 5L d'eau et ensuite utiliser la définition de C.

On a :
C=m.C_m , avec C_m=C_e or 1L d'eau a une masse de 1Kg donc m=5Kg ainsi
C=5×4,18 = 20,9 kJ/K
Et par définition la capacité calorifique de l'eau est l'énergie nécessaire pour élever la température de l'eau de 1°C donc Je trouve ainsi T

Oui, c'est bien cela que j'aurai plutôt écrit puisque c'est une variation de température que l'on cherche.

D'accord , Merci une fois de plus gts2