Inscription / Connexion Nouveau Sujet
circuit electirique
bonjours a tous j'aurais besoin de votre aide pour un exe de physique
1) quelle est la fonction de la diode (D) quant on ferme l'interupteur k, puis quand on l'ouvre?
J'ai des probleme sur cette question je ne sais pas ce que c'est une diode donc si vous pouviez m'expliquez ce que c'est et m'aidez sur cette premiere question
merci beaucoup
Une diode parfaite est un composant électronique qui se comporte comme une résistance infinie pour un courant voulant la traverser dans le sens cathode vers anode et qui se comporte comme une résistance nulle pour un courant voulant la traverser dans le sens anode vers cathode.
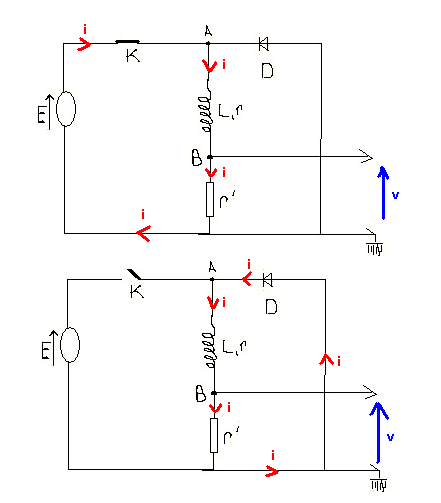
Avec l'interrupteur k fermé (dessin du haut), la diode est bloquée, elle n'est parcourue par aucun courant.
Il s'établit un courant i dans le circuit générateur µ , K , L,R et r'.
On peut trouver la fonction i(t) :
E - L.di/dt - ri - r'i = 0
L.i' + (r+r')i = E
i est solution de cette équation différentielle, avec i(0) = 0 (origine des temps au moment de la fermeture de K.)
On trouve: i = K.e^(-t.(r+r')/L) + E/(r+r')
Et avec i(0) = 0 --> K = -E/(r+r')
Donc finalement: i(t) = [E/(r+r')]*(1 - e^(-t.(r+r')/L))
Et v = r'i -->
v = [Er'/(r+r')]*(1 - e^(-t.(r+r')/L))
Si on attend suffisamment longtemps, i tends vers une valeur continue qui vaut E/(r+r') et v tend vers Er'/(r+r')
-----
A l'ouverture de l'interrupteur k et après (dessin du bas), le courant i passe maintenant dans le circuit L,r,r',Diode
En supposant la diode parfaite (sans chute), on trouve:
(en prenant ici l(origine des temps au mpement de l'ouverture de K)
L di/dt + (r+r')i = 0
i est solution de cette équation différentielle, avec i(0) = Io (qui vaut E/(r+r') si K a été préalablement fermé un temps suffisant).
on trouve: i(t) = Io.e^(-t.(r+r')/t)
Et si Io = E/(r+r'), on a: i(t) = (E/(r+r')).e^(-t.(r+r')/t)
et on a v(t) = r'.i = i(t) = (Er'/(r+r')).e^(-t.(r+r')/t)
Si on attend suffisamment longtemps, i(t) et v(t) tendent vers 0.
-----
Sauf distraction. 
merci beaucoup pourait tu me donner la tension de la risitance r'
parceque j'ai un livre ou il ya ecrit que la tension de la resistance U(r')=-U0*e-t/TAU
mais je sais pas comment il ont pu l'a trouver si tu pouvais m'expliquez **.
merci beaucoup
D'abord correction d'innattention.
Remplacer les quelques dernières lignes de ma réponse précédente par :
on trouve: i(t) = Io.e^(-t.(r+r')/L)
Et si Io = E/(r+r'), on a: i(t) = (E/(r+r')).e^(-t.(r+r')/L)
et on a v(t) = r'.i = (Er'/(r+r')).e^(-t.(r+r')/L)
Si on attend suffisamment longtemps, i(t) et v(t) tendent vers 0.
Dans cette phase, on a:
v(t) = r'.i = i(t) = (Er'/(r+r')).e^(-t.(r+r')/L)
En posant l/(r+r') = tau, on a:
v(t) = (Er'/(r+r')).e^(-t/tau)
Et si on appelle Uo la tension v en t = 0
--> v(0) = Uo = (Er'/(r+r')).e^(-0/tau)
--> v(0) = Uo = (Er'/(r+r')
Et alors v(t) = Uo.e^(-t/tau)
C'est la tension aux bornes de r' dans la phase où on ouvre interrupteur.
Il n'y a pas de raison d'avoir un - précédent le Uo, sauf si des présision d'énoncé n'ont pas été données.
-----

v(t) = r'.i = i(t) = (Er'/(r+r')).e^(-t.(r+r')/L)
je ne comprend pas d'ou tu as pris cette loi pourait u m'epliquez comment
je suis desoler de poser des question bete mais j'ai quelque probleme avec la leçon "dipole RL"
merci
C'est presque cela,, il s'agit plus exactement de :
v(t) = r'.i(t) = (Er'/(r+r')).e^(-t.(r+r')/L)
La loi d'Ohm est v = r'.i
Avec v la tension aux bornes d'une résistance r' traversée par un courant i.
Or, dans le début de l'exercice, on a montré que i = (E/(r+r')).e^(-t.(r+r')/L) et donc, on trouve:
v = r'.(E/(r+r')).e^(-t.(r+r')/L)
soit:
v = (Er'/(r+r')).e^(-t.(r+r')/L)

ca j'avais compris mais comment a tu entre U0 dans cette loi
normalement (Er'/(r+r'))=I0*r' parceque(E/(r+r')=I0
alors siltplait pourquoi tu as mit U0
Fichtre, j'ai mis Uo parce que tu as écrit ceci:
j'ai un livre ou il ya ecrit que la tension de la resistance U(r')=-U0*e-t/TAU
Uo est simplement la tension aux bornes de r' au moment t = 0 (donc au moment où on ouvre l'interrupteur K).
Dans mon message du 18/12/2007 à 11:28
On a trouvé (en cours de route):
i(t) = Io.e^(-t.(r+r')/L)
et comme v(t) = r'i(t), on a donc:
v(t) = r'.Io.e^(-t.(r+r')/L)
et en posant Uo = r'I0, on a:
v(t) = Uo.e^(-t.(r+r')/L)
Si on avait laissé l'interrupteur K fermé longtemps assez dans la première partie alors on a: Io = E/(r+r') et donc Uo = r'E/(r+r')
Dans ce cas, on trouve alors:
v(t) = Uo.e^(-t.(r+r')/L)
v(t) = (r'E/(r+r')).e^(-t.(r+r')/L)
-----

merci pour les reponse d'avant maintenant j'espere que tu pourais m'aidez pour le reste de l'exo
- le graph montre les variation de la tension Ur' (tension au borne de la risistance r') dé l'ouverture de l'interupteur
2) pourquoi le grph est comme ca?
voici ma reponse veuillez me corriger si je fais une faute :
Ur'=Ri. R etant une constante on se focalisera sur l'intensite "i"
la portion du graph qui est plate montre que i=I0 donc Ur'=E
la partie qui est decroisante montre que i est entrain de decroitre progresivement vers "0" et ca a cause de la bobine qui au moment d'ouvrir l'interupteur s'oppose a la disparition du courant ce qui donne cette forme au graph
voila j'espere que c juste j'attend une correction merci
vu que personne ne repond je vais continuer l'enonce de mon exo:
3)trouver la formule de la constante de temps (tau) pour le circuit
4)comment peut on la trouver en se servant du graph en savant que le temps de balayage est 2ms/div
trouver cette valeur
deduisez t1/2
aidez moi silvouplait a repondre a ces question merci beaucoup
Avec K fermé, j'ai montré que la tension aux bornes de r' se stabilisait à (r'E/(r+r')).
A l'ouverture de K la tension s'exprime par: v(t) = (r'E/(r+r')).e^(-t.(r+r')/L)
Si on représente v(t) sur un graphe à partir de ces expressions, on trouve exactement le dessin montré dans ton message du 18/12/2007 à 14:51
-----
La constante de temps tau du circuit est déduite aussi de l'expression v(t) = (r'E/(r+r')).e^(-t.(r+r')/L)
On a tau = L/(r+r')
-----
Pour trouver tau sur le graphe:
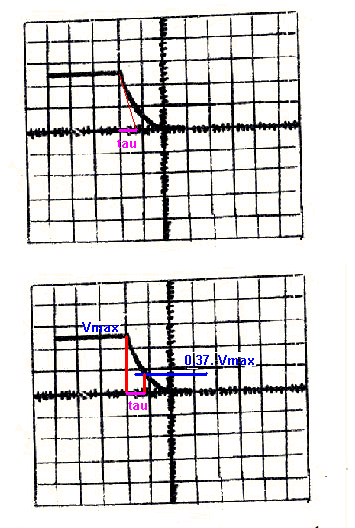
Manière 1: (dessin du haut)
Tracer la tangente à la courbe au moment de l'ouverture de K.
Cette tangente coupe l'axe des abscisses après le temps tau.
Manière 2: (dessin du bas)
Tau est le temps que met se signal pour redescendre à 0,37 fois sa valeur max.
On trouve tau = 0,8 division, soit 1,6 ms
-----
Sauf distraction. 




