Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Reprise d'études [tout]Lister tous les topics de physique - chimie
Niveau reprise d'études
Partager :

Cinématique Expression du vecteur vitesse dans la base sphérique

Posté par
hbx360 06-01-22 à 22:05

Bonjour,

En regardant une vidéo sur les coordonnées du vecteur vitesse dans la bas sphérique je ne comprends pas la décomposition du vecteur \vec{e_{r}}

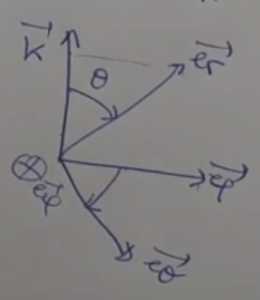
Voici une image de la vidéo :

Ce que je ne comprends pas c'est comment on fait pour trouver cos\theta \vec{k} et sin\theta \vec{e_{\rho }} qui sont les projeter du vecteur \vec{e_{r}}.

Parce que dans l'image là ou on voit la base sphérique si on projette le vecteur \vec{e_{r}} sur l'axe des z (ou  \vec{k} est le vecteur unitaire pour l'axe des  z dans la base cartésienne) ne devrait-on pas plutôt trouver cos\theta \vec{e_{r}} = \vec{k} et sin\theta \vec{e_{r}} = \vec{e_{\rho }}.

Car si on se base sur l'angle \thetaet qu'on projette sur l'axe des z le vecteur  \vec{e_{r}} on devrait faire  cos\theta est égale au côté adjacent donc \vec{k} sur hypoténuse donc \vec{e_{r}} ce qui devrait nous donner
cos\theta = \frac{\vec{k} }{\vec{e_{r }}} \Leftrightarrow cos\theta {\vec{e_{r }}} = \vec{k} au lieu de \vec{e_{r}} = cos\theta \vec{k}

Voilà en espérant avoir été assez claire ?

Merci d'avance.

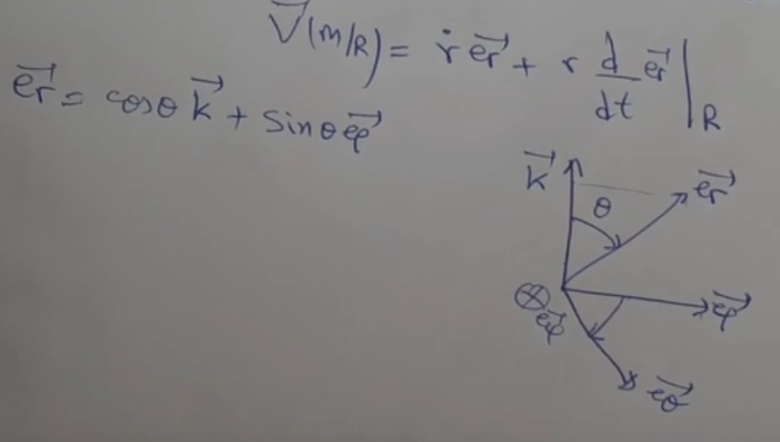
Cinématique Expression du vecteur vitesse dans la base sphérique

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 06-01-22 à 22:46

Bonsoir

Citation :
ce qui devrait nous donner
cos\theta = \frac{\vec{k} }{\vec{e_{r }}} \Leftrightarrow cos\theta {\vec{e_{r }}} = \vec{k} au lieu de \vec{e_{r}} = cos\theta \vec{k}

Cela est nécessairement faux car ces deux vecteur ne sont pas colinéaires.En revanche : \overrightarrow{e_{r}}=\cos\left(\theta\right).\overrightarrow{k}+\sin\left(\theta\right).\overrightarrow{e_{\rho}} me semble correct compte tenu du schéma que tu as fourni. Ce schéma en 3D pourra peut-être t'aider. Pour les vecteurs unitaires, il suffit de remplacer "u" par "e"... Autre document éventuellement utile :

Cinématique Expression du vecteur vitesse dans la base sphé

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 06-01-22 à 22:48

Merci pour ta réponse je vais voir le lien.

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 06-01-22 à 23:13

J'ai regardé le pdf du lien plus la vidéo mais je ne comprends pas j'arrive toujours au même résultat savoir :

cos\theta = \frac{\vec{k} }{\vec{e_{r }}} \Leftrightarrow cos\theta {\vec{e_{r }}} = \vec{k} au lieu de \vec{e_{r}} = cos\theta \vec{k}

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 06-01-22 à 23:41

On est bien d'accord que c'est le vecteur \vec{e_{r}} que l'on projette sur le vecteur unitaire  \vec{k} et non l'inverse parce que l'inverse ça marche si je projette \vec{k} sur \vec{e_{r}} alors j'obtiens bien :

cos\theta = \frac{\vec{e_{r}}}{\vec{k} } \Leftrightarrow \vec{e_{r}} = cos\theta \vec{k} idem pour le sinus.

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 12:16

Écrire que le rapport de deux vecteurs est un réel (ici cos() ) suppose les deux vecteurs colinéaires, ce qui évidemment est faux ici !
Je ne vois pas quoi ajouter à mon message du 06-01-22 à 22:46 pour te convaincre ! Le deuxième document que je t'ai fourni détaille la méthode pour exprimer un vecteur dans une base donnée. Il te faut peut-être aussi revoir ton cours de trigonométrie sur les sinus et cosinus...

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 13:44

Merci de ton aide, en fait je pense que je me suis mal exprimé, je n'affirme pas que

cos\theta = \frac{\vec{k} }{\vec{e_{r }}} \Leftrightarrow cos\theta {\vec{e_{r }}} = \vec{k}

est vrai. Mais comme je ne comprends pas comment on arrive à ce résultat

cos\theta = \frac{\vec{e_{r}}}{\vec{k} } \Leftrightarrow \vec{e_{r}} = cos\theta \vec{k}

C'est pour ça que je demande de l'aide.

J'ai refait les calcules et malheureusement je suis tombé sur une impasse puisque je trouve le résultat

cos\theta = \frac{\vec{k} }{\vec{e_{r }}} \Leftrightarrow cos\theta {\vec{e_{r }}} = \vec{k} au lieu de \vec{e_{r}} = cos\theta \vec{k} \\   

et je n'arrive pas à comprendre comment on l'obtient.

J'ai bien regardé les liens que tu m'as données mais j'arrive toujours à ce même résultat faux.

Peux-tu me dire ci c'est juste :
Pour moi :
- \vec{e_{r}} c'est l'hypothénus et
- \vec{k} c'est le côté adjacent

et donc si je fais la relation entre le cosinus et les côtés de l'angle je trouve :

cos\theta = \frac{\vec{k} }{\vec{e_{r }}} c'est pour ça que j'arrive pas à comprendre comment on fait pour isoler {\vec{e_{r }}} et arrivé à la bonne expression.

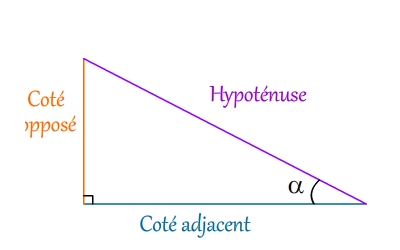
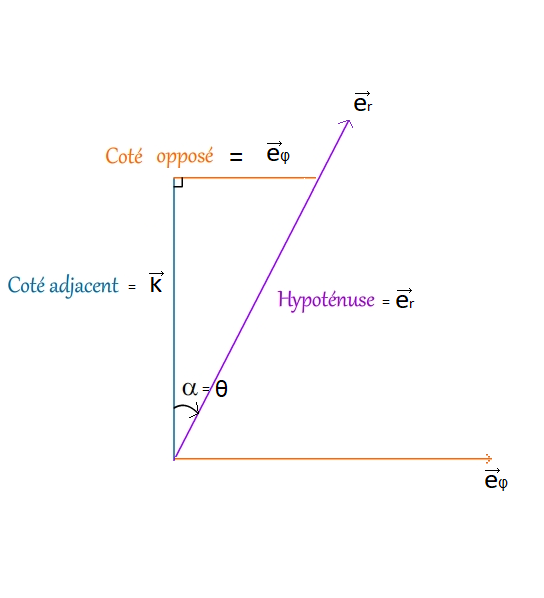
J'ai bien regardé ton dernier lien donc si je fais un parallèle avec cette image qui vient de ton lien et aussi avec le schéma de l'image de la vidéo de la base sphérique voici ce que ça donne :

Et donc on vois bien que {\vec{e_{r }}} est bien l'hypothénus.

Voilà, ou peut-être éventuellement me donner la démonstration de  comment on arrive à ce résultat

\vec{e_{r}} = cos\theta \vec{k}

parce que là je sèches malgré ton aide.

Cinématique Expression du vecteur vitesse dans la base sphé

Cinématique Expression du vecteur vitesse dans la base sphé

Cinématique Expression du vecteur vitesse dans la base sphé

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 14:38

Citation :

\vec{e_{r}} = cos\theta \vec{k}

CETTE FORMULE EST FAUSSE. JE T'AI EXPLIQUÉ POURQUOI À PLUSIEURS REPRISES DANS MES MESSAGES PRÉCÉDENTS...
Je t'ai fourni le résultat correct dans mon message du  06-01-22 à 22:46. Je le recopie :

\overrightarrow{e_{r}}=\cos\left(\theta\right).\overrightarrow{k}+\sin\left(\theta\right).\overrightarrow{e_{\rho}}
Concernant la figure que tu fournis : deux remarques :
1° : tu confonds les vecteurs unitaires \overrightarrow{e_{\varphi}} et \overrightarrow{e_{\rho}} . Le vecteur \overrightarrow{e_{\varphi}} est perpendiculaire au vecteur \overrightarrow{e_{r}}. Le vecteur \overrightarrow{e_{r}} ne s'exprime donc pas en fonction de \overrightarrow{e_{\varphi}} ; Sur la figure que tu fournis dans ton dernier message, il faut donc remplacer \overrightarrow{e_{\varphi}} par \overrightarrow{e_{\rho}} . Ce dernier vecteur n'est pas sur mon schéma en 3D : c'est un vecteur unitaire ayant la direction et le sens du vecteur \overrightarrow{OM}.

2° tous les vecteurs que tu considères sont des vecteurs unitaires, donc des vecteurs de même norme égale à 1. Cela n'apparaît pas sur ta figure : tes vecteurs unitaires ont tous des normes différentes !

Posté par
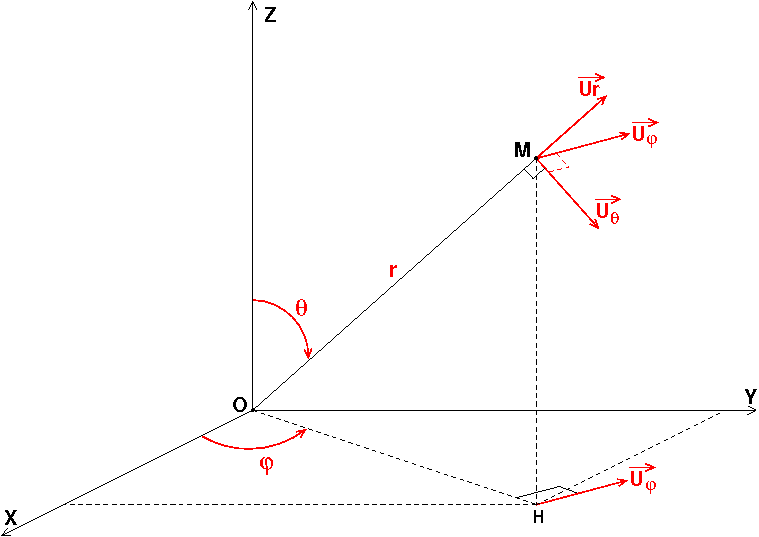
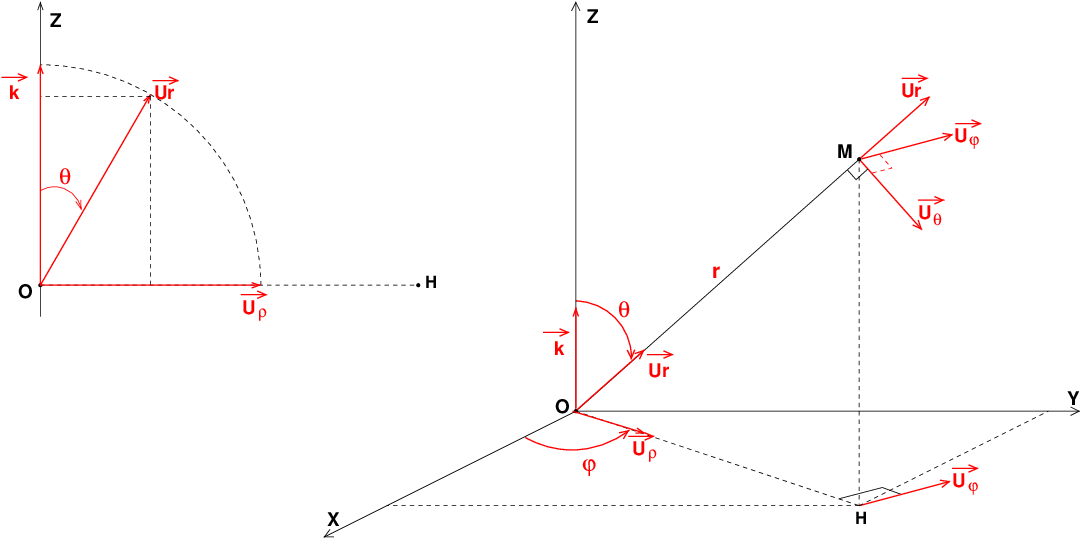
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 15:05

D'accord, je me rend compte que  j'avais pas percuté pour

\overrightarrow{e_{r}}=\cos\left(\theta\right).\overrightarrow{k}+\sin\left(\theta\right).\overrightarrow{e_{\rho}}

Mais comment tu obtiens :

\cos\left(\theta\right).\overrightarrow{k} et \sin\left(\theta\right).\overrightarrow{e_{\rho}}

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 15:32

J'ai complété mon schéma en 3D et ajouté sur le coté gauche un schéma en 2D représentant les vecteurs unitaires du plan (OHz).

Cinématique Expression du vecteur vitesse dans la base sphé

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 16:12

Merci,

Par rapport à tes schémas peux-tu me dire si cela est exact :

\vec{U_{r}} = U_{r_{z}}\times \vec{k} + U_{r_{\rho}}\times \vec{e_{\rho }}

Ou
U_{r_{z}} est la distance entre le point O est le projeté de  \vec{U_{r}} sur l'axe des z et
U_{r_{\rho}} est la distance entre le point O est le projeté de \vec{U_{r}} sur l'axe \vec{U_{\rho }}

Pour calculer U_{r_{z}} et U_{r_{\rho}} on fait :
{\parallel \vec{U_{r}}\parallel } = 1

cos\theta = \frac{U_{r_{z}}}{\parallel \vec{U_{r}}\parallel } = \frac{U_{r_{z}}}{1 } \Leftrightarrow cos\theta \times 1= U_{r_{z}} \Leftrightarrow cos\theta = U_{r_{z}}

sin\theta = \frac{U_{r_{\rho}}}{\parallel \vec{U_{r}}\parallel } = \frac{U_{r_{\rho}}}{1 } \Leftrightarrow sin\theta \times 1= U_{r_{\rho}} \Leftrightarrow sin\theta = U_{r_{z}}

Et ensuite on remplace  dans

U_{r_{z}}\times \vec{k} + U_{r_{\rho}}\times \vec{e_{\rho }}

U_{r_{z}} par cos\theta  et


U_{r_{\rho}} par sin\theta ce qui donne :

\vec{U_{r}} = cos\theta \times \vec{k} +sin\theta \times \vec{e_{\rho }}

Posté par
mmalou Webmasterre : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:26

Bonjour,

la demande en parallèle sur plusieurs forums n'est pas des plus élégantes

attentionextrait de c_faq la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

attentionextrait de c_faq la FAQ du forum :

Q30 - J'ai été averti ou banni, pourquoi, et que faire ?

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:36

Bonjour et merci mmalou pour ta vigilance.
Je ne peux qu'être d'accord évidemment avec le contenu de ton message...

Posté par
mmalou Webmasterre : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:40

Non, mais...tu lui expliques depuis hier soir en long, en large et en travers, et il ose poster ailleurs aujourd'hui ...
Un peu se savoir vivre ne ferait pas de mal à certains.

Posté par
vanoisere : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:46

J'apprécie le "s" à certains...

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:48

Bin désolé, mais comme je n'arrivais pas à comprendre les explications j'ai été sur un autre forum, et oui j'avais aussi oublié ce point de la charte qu'on ne pouvais pas posté sur un autre forum le même sujet.

mmalou dans mon dernier message je pense être dans le vrai mais si
vanoise (que j'ai remercié d'ailleurs mainte fois aussi, ce que tout le monde ne fait pas forcé quand il on eu une réponse ) m'avais expliqué ce que j'ai mis dans mon dernier message j'aurai même pas été sur un autre forum, c'est cette (ce genre de) réponse que j'attendais.


mmalou tu dis :
"Non, mais...tu lui expliques depuis hier soir en long, en large et en travers, et il ose poster ailleurs aujourd'hui ...
Un peu se savoir vivre ne ferait pas de mal à certains. "

Merci de ne pas me prêter ce genre d'intention qui est complétement fausse et insultante je ne comprenais ça peut arrivé il me manquait juste la démonstration de pourquoi on arrive à tel résultat.

Posté par
mmalou Webmasterre : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 17:51

certes...mais justement savoir dire ce qu'on ne comprend pas, fait partie du cheminement vers la compréhension

était-ce si difficile de dire à vanoise ce qui n'était pas clair pour toi ?

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 07-01-22 à 18:03

Bin j'ai essayé mais j'y suis pas arrivé
Je suis d'accord avec toi mmalou mais c'est pas toujours facile d'expliquer.

L'aide apporté par vanoise m'a aidé mais pas au point de comprendre, donc j'ai continué à cherché sur internet et je pense en attendant confirmation de vanoise que je dois plus être loin de la solution.

Après je suis désolé si j'ai blessé vanoise car je comprends que si on s'investit pour aider quelqu'un et de voir la personne aller ailleurs que sa peut blesser, je reconnais que j'ai fait une faute.

Posté par
gbm Webmasterre : Cinématique Expression du vecteur vitesse dans la base sphé 08-01-22 à 10:46

Bonjour,

C'est vrai qu'on peine culturellement à oser dire qu'on n'a pas compris ou qu'on ne sait pas, mais c'est de cette façon qu'on progresse justement, y compris dans le monde professionnel !

Déjà c'est bien que tu reconnaisses ton erreur et que tu présentes tes excuses à vanoise.

Si tu souhaites continuer l'échange avec lui, la moindre des choses serait d'aller sur l'autre forum et d'admettre que tu reçois déjà de l'aide ici.

Bon WE,

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 08-01-22 à 10:54

Oui gbm tu as raison c'est ce que je vais faire.

Posté par
hbx360re : Cinématique Expression du vecteur vitesse dans la base sphé 08-01-22 à 11:02

J'ai demandé la suppression du post sur l'autre forum voilà.

Bon week-end à tous.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !