Inscription / Connexion Nouveau Sujet
Cinématique et collision
Bonsoir à tous, j'ai un dm à rendre pour demain, tout est fait, néanmoins en vérifiant il se trouve que j'avais bloqué sur une partie de calcul, et j'ai oublié d'y revenir, et je bloque toujours. Ce n'est pas grand chose, ça doit se régler je pense en 5 minutes mais là je ne vois pas pourquoi je ne trouve pas le résultat que je devrais trouver (que j'ai trouver grâce à la calculette). Voici l'énoncé:
Une voiture de largeur L est en mouvement le long d'un trottoir rectiligne d'axe (Ox). Un piéton décide de traverser la route au moment où la voiture se trouve à une distance D. Le mouvement du piéton est rectiligne, uniforme, de vecteur vitesse incliné d'un angle φ par rapport à l'axe (Oy)
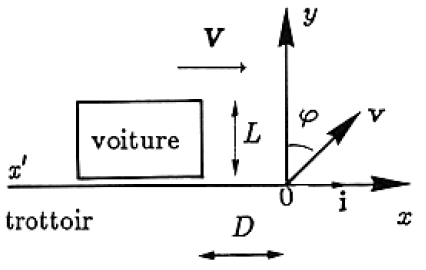
La voiture se déplace à la vitesse constante =V*
1. L'angle φ étant fixé, exprimer la valeur limite de permettant d'éviter une collision.
-> Alors j'ai donné les coordonnées de la voiture: xv=Vt-D et yv=L
Les coordonnées du piéton: xp=v*sin(φ)*t et yp=v*cos(φ)*t
La position limite pour rentrer en collision est:
xp=xv <=> v*sin(φ)*t=V*t-D
yp=yv <=> v*cos(φ)*t=L donc t=L/(v*cos(φ))
donc v*sin(φ)*L/(v*cos(φ))=V*L/(v*cos(φ))-D
A la calculette je trouve v=LV/(D*cos(φ)+L*sin(φ))
Donc pour éviter la collision v>LV/(D*cos(φ)+L*sin(φ))
Or je n'arrive pas à passer de mes équations au résultat, si quelqu'un peut m'aider ça serait vraiment gentil.
2. En considérant comme une fonction de φ, déterminer la valeur de φ pour laquelle la vitesse limite est minimale. Exprimer la valeur correspondante de la vitesse.
-> J'ai réussi cette question. J'ai dit qu'il fallait en fait trouver le max de D*cos(φ)+L*sin(φ).
Soit ƒ la fonction φ -> D*cos(φ)+L*sin(φ)
ƒ'(φ)=-D*sin(φ)+L*cos(φ)
donc tan(φ)=L/D et cos(φ)=1/=D/
Donc v=LV/(cos(φ)(D*cos(φ)+L*tan(φ)))=LV/
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()

 /cos
/cos 
