Inscription / Connexion Nouveau Sujet
Cinématique du point
Salut, voilà,un exercices où je rencontre quelques problèmes ;
Énoncé :
Sur une autoroute rectiligne où la vitesse est limitée à 110 km/h,un automobiliste roule à la vitesse constante de 134km/h.Un motard averti par radio,démarre d'un lieu situé à une distance d=390m de l'automobiliste devant celui-ci.Roulant alors dans le même sens que l'automobiliste,le motard atteint la vitesse de 62km/h en 10s.
On prendra pour origine des espaces,le lieu où se trouvait l'automobiliste au moment du démarrage du motard,et l'instant correspond comme origine des dates.
Consignes:
1) Déterminer l'accélération a du motard ;
2)Établir les équations horaires X1(t) et X2(t) des mouvements respectivement de l'automobiliste et du motard.;
3) Déterminer l'instant t où les deux mobiles sont côte à côte.;
4)A l'instant t, le motard fait signe à l'automobiliste de s'arrêter.Ce dernier créneau régulièrement et s'immobilise après avoir parcouru 390m pendant la phase de freinage.
4.1) Calculer l'accélération a de l'automobiliste pendant cette pha se.
4.2) Combien de temps dure cette phase?
Pour le 1,je trouve a=2m/s^2,
pour le 2,je ne suis pas sûr du résultat,et pour le reste, je ne sais pas comment faire.
Pouvez vous m'aider ?
***Sujet aéré (pour changer)***
1)a=(v2-v1)/(t2-t1) AN:a=(72/3,6-0)/(10-0) alors a=2m/s^2.Pour le 2)X1(t)=Vx1(t)+xo=40t et X2(t)=1/2axt^2+Vox+xo=1/2×2t^2=t^2
Merci à l'avenir de soigner la mise en page : Tu es difficilement lisible.
Question 1
A condition de définir ce que sont pour toi : a, v2, v1, t2 et t1 on peut arriver en effet à l'expression que tu as obtenue.
On peut aussi dire :
Si on appelle Δv la variation de vitesse du motard pendant la durée Δt et si on suppose que l'accélération " a " du motard est constante alors
a = Δv / Δt
Ton application numérique :
a=(v2-v1)/(t2-t1) AN:a=(72/3,6-0)/(10-0) alors a=2m/s^2.
Je ne trouve dans l'énoncé aucune donnée correspondant à ton " 72 "
Explique toi.
Question 1 :
a = Δv / Δt
Δv = 17,22 - 0 = 17,22m/s
Δt = 10s
On trouve bien que a  1,72m/s²
1,72m/s²
Question 2 :
L'énoncé demande clairement d'établir les équations horaires.
Tu ne les a pas établies, tu les a balancées sans la moindre justification.
X1(t) = 37,22 * t est une résultat exact.
X2(t) = 0,86 * t² est faux
Penser à la position du motard à la date t=0 pour corriger.
X2(t)=1/2axt^2+voxt+xo car le mouvement du motard est rectiligne uniformément varié. Ensuite X2(t)=1/2×17,22t^2+0+0;
X2(t)=8,61t^2
Dans ton post du 30-01-21 à 12:32 tu trouvais :
X2(t) = 0,86 t²
Dans celui du 30-01-21 à 15:50 tu trouves
X2(t) = 8,61 t²
Les deux sont faux, mais le premier est plus proche de la bonne réponse que le second.
Quelle est l'abscisse du motard à la date t=0
a) D'après l'énoncé ?
b) D'après l'équation horaire que tu trouves ?
car, bien entendu, ces deux abscisses doivent être identiques
Ta réponse, non justifiée selon tes mauvaises habitudes, serait exacte si le véhicule concerné était l'automobile.
Pourquoi est elle fausse ?
Parce que on cherche l'équation horaire X2(t) du motard et non de l'automobile et que à la date t=0 (origine des dates) les deux mobiles ne se trouvent pas au même endroit et n'ont donc pas la même abscisse.
Je te conseille de lire, relire puis lire à nouveau l'énoncé et ensuite de faire et de poster un schéma représentant les positions de l'automobile et du motard à la date t=0 telle qu'elle est définie dans l'énoncé.
Complète ton schéma en faisant apparaître les abscisses des deux mobiles à cette date t=0
Cela devrait t'aider à obtenir l'équation horaire correcte du motard.
Ok, A t=0;X1o=-390m
Toujours pas, mais tu progresses.
L'énoncé, si on le lit attentivement, précise que :
"le motard averti par radio,démarre d'un lieu situé à une distance d=390m de l'automobiliste devant celui-ci"
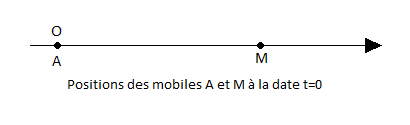
Je te joins le schéma que je te suggérais de faire représentant la situation à la date t=0
Le point O représente l'origine des espaces
Les points A et M désignent les positions de l'automobiliste et du motard.
Ah oui, j'avais confondu la position du motard à celle de l'automobiliste.On aura donc,
A t=0;X1o=390m
C'est bien ça.
Tu as donc tous les éléments pour écrire correctement l'équation horaire X2(t) du motard.
OK
Question 3 :
Tu as donc maintenant les deux équations horaires :
X1(t) = V1*t
et
X2(t) = (1/2)*a*t² + d
V1=135km/h  37,2m/s , a
37,2m/s , a 1,72m/s² et d=390m sont connus, mais il n'est pas indispensable de passer immédiatement aux valeurs numériques.
1,72m/s² et d=390m sont connus, mais il n'est pas indispensable de passer immédiatement aux valeurs numériques.
A la date t = θ les deux mobiles se trouvent côte à côte donc :
X1(θ) = X2(θ)
On en déduit la valeur de la date θ
Je te laisse faire ....
Oui, j'ai obtenu avec trois chiffres significatifs et sans arrondir les valeurs de "a" et de V1:
 1 = 17,8s et
1 = 17,8s et  2 = 24,4s
2 = 24,4s
Je viens seulement de remarquer que tes valeurs de  étaient négatives.
étaient négatives.
Ce n'est pas possible car cela signifierait que la rencontre Automobiliste / Motard aurait lieu avant l'origine des dates donc avant le démarrage du motard.
L'équation X1( ) = X2(
) = X2( ) donne :
) donne :
V1* = (1/2) * a *
= (1/2) * a *  ² + d
² + d
(1/2) * a *  ² - V1*
² - V1* + d = 0
+ d = 0
avec a = (31/18) m/s²  1,72 m/s²
1,72 m/s²
V1 = 134 km/h = (335/9) m/s
d = 390 m
Donc (31/36)  ² - (335/9)
² - (335/9)  + 390 = 0
+ 390 = 0
soit après simplification :
31  ² - 1340
² - 1340  + 14040 = 0
+ 14040 = 0
On obtient 2 racines positives :
 1
1  17,8s et
17,8s et  2
2  24,4s
24,4s

 =-17,79s et
=-17,79s et  =-25,48s
=-25,48s
