Inscription / Connexion Nouveau Sujet
cinématique du point
Bonjour je voudrais quelqu'un pour aider s'il vous plait
un voyageur en retard court le long d'un quai a la vitesse constante de v=6m/s
1 )quand il est a 20m du dernier wagon du train qui démarre avec accélération constante a=+1m.s-2 (le train et le voyageur ont des trajectoires parallèles. )
1.définir le repère dans le le mouvement est étudié.préciser sur le schéma les positions, les dates et les vitesses.
2.écrire dans le meme repere les équations hohoraires du voyageur et du wagon considéré comme des point matériel.
3.monter que le voyageur ne peut pas rattraper le train.
4.quelle sera la distance minimal entre le voyageur et le derrière du wagon
Bonjour,
Je te souhaite tout d'abord la bienvenue sur le forum. Comme tu as pu très certainement le lire dans le topic [A LIRE AVANT D'AGIR], l'objectif du forum n'est pas de faire l'exercice à ta place.
On s'attend en effet à ce que tu nous proposes tes pistes de résolution, par exemple ici :
- en faire un schéma simplifié de chaque situation étudié (sous Visio ou Paint par exemple, que tu peux poster avec le bouton "Img" sous le cadre dans lequel tu rédiges tes messages) ;
- préciser le référentiel d'étude pour chaque cas ;
- rappeler comment écrire les équation horaires à partir des coordonnées des vecteurs accélération, vitesse et position (suivant le repère d'étude choisi).
Pour ce faire, je te recommande vivement de lire attentivement cette fiche avant de commencer (clique sur la maison) : ![]() Décrire un mouvement
Décrire un mouvement
Au travail !

bonjour
Les équations horaires
je pense que si le mouvement s'effectue sur [bX[/bY] donc v (y)=0 donc sa devient à a=0 v=6t +20
Voile se que jai pu faire
1 ) le mouvement le fait dans une repère cartésien (o.i.j) ((je ne vois pas ici un schéma ))
2) les équations horaires
pour le voyageur
à t=0 v=Voi=>v=6i +c or x=xo=c et xo =20 cequi donne X (t)=6t +20 et a=0
pour le wagon [sub][/sub]
à t=0 a=1=>V=t entre x (t)=1÷2t^2
Je m'a suis bloquer à la 3e et4e question
mais EST CE QUE MON RAISON NE EST CORRECTE? ?
Bon, reprenons :
1. Le référentiel d'étude est le quai de la gare :
- O : début du quai (x = 0 m) ;
- le passager finit par rejoindre le bout du train l'instant t à x = 20 m.
Schéma de la situation :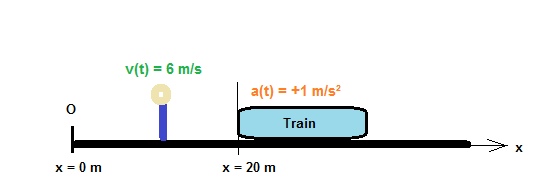
2. Lorsque le voyageur rejoint le train :
v(t) = +6 m/s
=> x(t) = 6.t + 20
Lorsque le train démarre (vitesse initiale nulle) :
a(t) = +1 m/s²
=> v(t) = +t + 0
=> x(t) = 1/2.t² + 20
Je te conseille de faire un tracé des deux graphiques en fonction du temps.
Je te laisse conclure


