Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour j'ai juste besoin d'aide sur la question sur les caractéristiques du vecteur vitesse Vp et aussi comment comparer ces deux vecteur mentionnés voici en dessous le schéma des deux vitesses.
Exercice
Les équations horaires du mouvement d'an mobile M relativement à un repère d'espace R (0)
x = 2t et y = f(t) (t>0). L'équation cartésienne de la trajectoire est I = - 5/4 * x ^ 2 + 2x
13 Représenter l'allure de la trajectoire
2) Déterminer l'expression de l'ordonnée y =t(0 sdu mobile.
a) Déterminer los composantes du vecteur vitesse V en fonction du temps
b ) A quelle date la direction du vecteur vitesse est horizontale, en déduire los coordonnées du sommet 5 de la
trajectoire Calculer la valeur de la vitesse en ce point.
3) Donner l'expression du vecteur accélération a. Conclure
4) Calculer le rayon de courbure de la trajectoire au sommet S de la trajectoire
5) Déterminer les phases du mouvement.
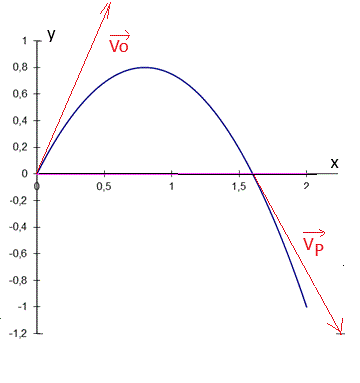
6) Déterminer l'abscisse du point ^ prime (P ne O ) intersection de la trajectoire avec l'axe os. Quelles sont les caractéristiques du vecteur vitesse V_{p} en ce point ? Comparer ce vecteur au vecteur V_{0} (direction, valeur). Représenter ces deux vecteurs sur la trajectoire. (Echelle de votre chois)
Bonjour,
2a)
y(x) = 5x² + 2x
et x = 2t
--> y(t) = …
la composante suivant l'axe des x du vecteur vitesse est Vx(t) et se trouve en dérivant x(t) par rapport au temps ---> Vx(t) = d(2t)/dt = 2
la composante suivant l'axe des y du vecteur vitesse est Vy(t) et se trouve en dérivant y(t) par rapport au temps ---> Vy(t) = ...
2b)
La vitesse est horizontale pour la valeur de t telle que Vy(t) = 0 --> pour t = …
Cette valeur de t trouvée, on peut calculer Vx et Vy pour cette valeur de t et en déduire les coordonnées du sommet de la trajectoire mais aussi la valeur (norme) de la vitesse en ce point.
Essaie et écris ce que tu trouves sur le site.
Bonjour
J'ai pas compris, j'ai déjà placé les vecteurs il me reste à comparer leur direction comment faire cela ?
Bonjour,
y(x) = -5/4 x² + 2x
et x = 2t
--> y(t) = -5t² + 4t
y'(t) = -10t + 4
x'(t) = 2
Donc le vecteur vitesse en fonction du temps est :
La trajectoire coupe l'axe des abscisses pour - 5/4 * x ^ 2 + 2x = 0 donc (outre x = 0) pour x = 1,6, soit donc à l'instant t = x/2 = 0,8 (unité de temps)
Le vecteur vitesse à cet instant est donc :
,
Le module de la vitesse à cet instant est :
unités de vitesse
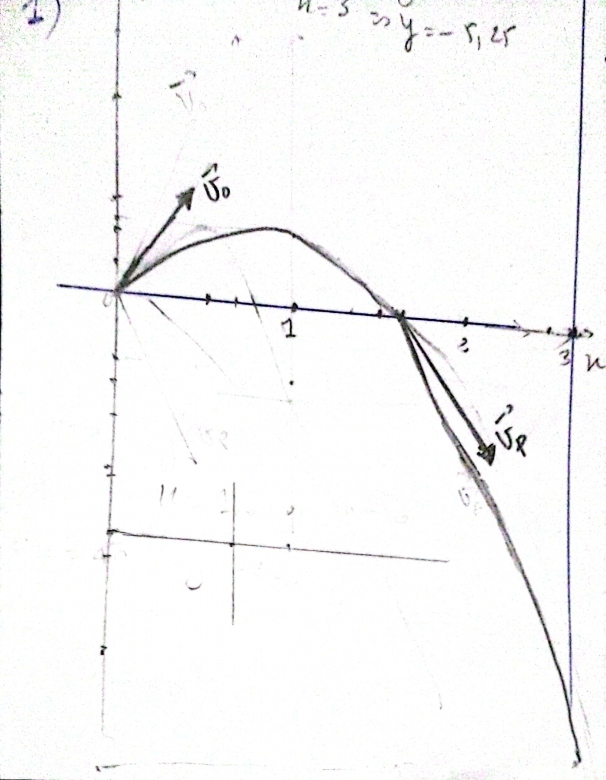
On a maintenant les 2 composantes suivant Ox et Oy du vecteur vitesse au point P et on peut le représenter sur le graphe de la trajectoire.
On procède de la même façon pour le vecteur vitesse au point O
Et on devrait avoir ,
donc
unités de vitesse
On remarque que , donc les vitesses en ces points ont la même valeur … mais sont évidemment de direction différentes.