Bonjour
Cela ressemble à la deuxième partie de l'exercice précédent.
Écris les équation sous leur formes générales :
v=a.t+v_o
x=(1/2)a.t²+v_o.t+x_o
Tu as deux inconnues ; il te faut deux équations déduites des données.

Bonjour, bon je vous épargne les calculs mais je résume 1)Vo= 8m/s et Xo=-7m
2)xt=-t²+8t-7 et Vt=-2t+8

Nous sommes d'accord ! Cela t'aidera peut-être : voici la courbe représentant les variations de l'abscisse de M1 en fonction de t.

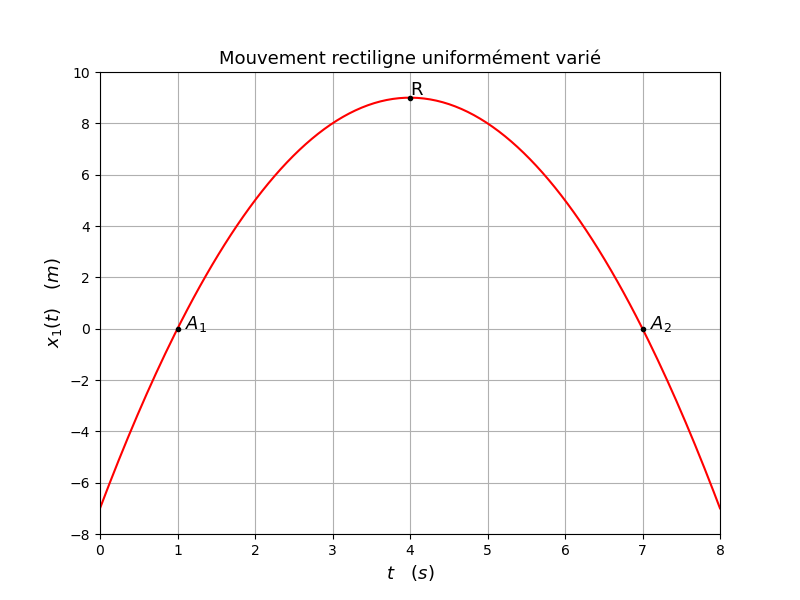
Bon pour être franc j'ai déjà fait l'exercice et d'après ton graphe je confirme que j'ai trouvé car ton graphe à répondu à la question 3 et 4 si on regarde bien mais c'est la façon dont j'ai procédé qui me fait douter je m'explique :
Pour la question 3) on nous dit de montrer que le mouvement comporte deux phases effectivement elle comporte deux phases une phase de décélération puis une phase d'accélération comment je l'ai trouvé c'est simple vous me direz après si c'est adéquat ou on peut procéder d'une autre manière :
Bon ce que j'ai fait c'est que j'ai pris différente dates t=0;1;2;4;6;7s puis je me suis proposé d'étudier le mouvement de M sur ces différents temps :
A t=0 ;
À t=1s;
À t=2s;v=4..
À t=4s;v=0..
Puis à t= 6s;v=-4..
À t=7s;v=-6i
Puis j'ai conclu d'après cette étude le mouvement est décéléré de t=0 à t=4s puis accélérer de t=4 à 7s
Dans la question 4 on va calculer la distance entre t=1s a 7s en premier lieu j'ai calculé les abscisses au temps respectifs on constate
At=1s; x=0 et à t=7s;x=0 donc on peut en conclure que la voiture ou le mobile a fait un trajet jusqu'à t  égal à 4s pour ensuite faire un demi-tour et arrive à sa position initiale à t=7s  donc pour connaître la distance D parcourue entre 1 et 7s j'ai calculé la distance parcourue (D/2) entre t=1 a 4s : D/2= x(t=4)-x(t=1)=9-0=9
qu'est ce que vous dites du chemin emprunter.

Ce que tu as fait est globalement correct. Pour l'étude des deux phases, il y a un peu plus rapide sachant que le mouvement est retardé si v.a<0 et accéléré si v.a>0. Comme ici : a<0 :
la phase retardé correspond à v>0 donc 0<t<4 s
la phase accéléré correspond à v<0 donc à t>4s.

Oui effectivement il y a plus rapide mais ce qu'on peut retenir c'est que je croyais au début que lorsqu'on a une phase de décélération l'accélération tangentielle est négative et lorsqu'on a une phase d'accélération dans ce cas l'accélération tangentielle  est positive mais ce que je croyais c'était pas ça on peut aussi bien avoir une phase d'accélération et de décélération en conservant un vecteur accélération tangentielle donc de signes négatifs comme notre cas.

De façon générale un mouvement accéléré correspond à un carré du vecteur vitesse croissant au cours du temps donc à une dérivée par rapport au temps de ce carré positive. Je te laisse démontrer que cela correspond à :


Pour un mouvement rectiligne, l'accélération se confond avec l'accélération tangentielle.

Ok merci