Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Cinématique

Posté par
Xenoverse 12-07-25 à 22:41

Bonjour j'ai besoin d'aide sur la question 5 de l'exercice merci.
exercice :
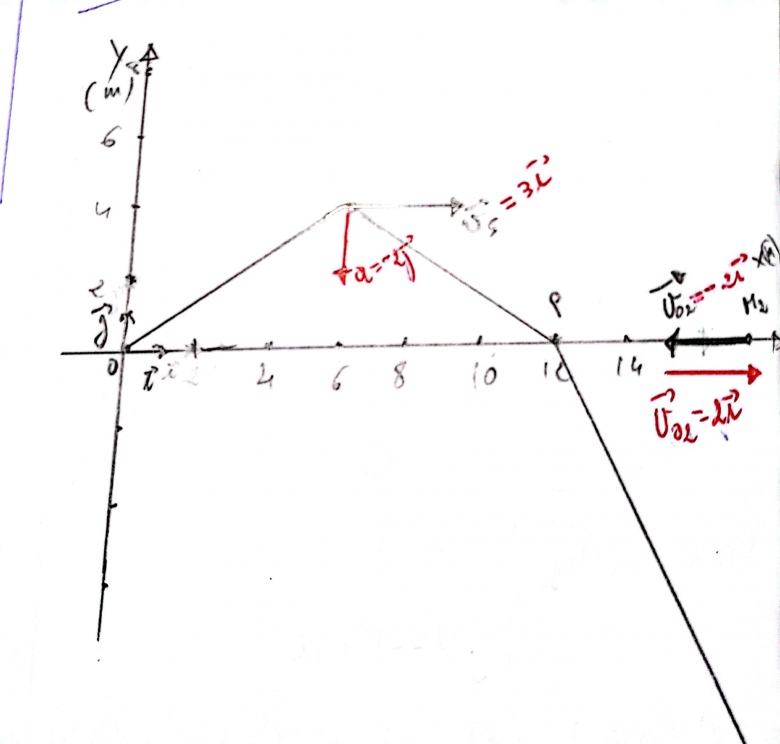
Un mobile M1 est en mouvement relativement au repère d‟espace R
( O, i, j )
, son vecteur
vitesse est :
V 3i ( -2t+ 4)j
1°/ Donner les lois horaires du mouvement sachant qu‟à l‟origine des temps, le mobile passe
par l‟origine O.
2°/ Etablir l‟équation cartésienne de
la trajectoire.
3°/Etablir l‟expression du vecteur
accélération
1 a .
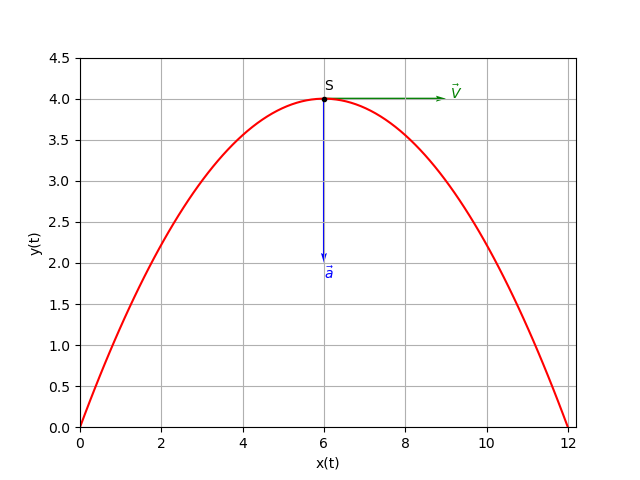
Le représenter sur la trajectoire de la
figure.
4°/ A quelle date la direction du
vecteur vitesse est horizontale ? En
déduire les coordonnées (xs ; ys) du
sommet S de la trajectoire ainsi que la
valeur de la vitesse en ce point.
Représenter ce vecteur vitesse.
5°/ Calculer :
Le rayon de courbure de la trajectoire à la date
t=2s.
L‟abscisse
Xp du mobile lorsque celui-ci repasse par l‟ordonnée y = 0.
La valeur de la vitesse
Vp
du mobile en ce point.
6°/ Un deuxième mobile M2 en mouvement rectiligne uniformément varié sur l‟axe ox du repère R
( O, i, j )
, passe par le point d‟abscisse x = 20 m à l‟instant t=0 avec une vitesse
V _0_2 =2\vec{i }.
Calculer la valeur algébrique de l‟accélération de M2 pour qu„il rencontre M1 au point x = 12

Posté par
phyelec78re : Cinématique 13-07-25 à 00:44

Pour la question 5)
-rayon de courbure il faut connaitre x et y à t= 2s : R=\sqrt{x^2+y^2

- pour mettez y=yp=0 dans l'équation horaire

-pour Vp ( il s'agit de module de la vitesse), appliquez la formule du cours .

Posté par
vanoisere : Cinématique 13-07-25 à 14:38

Citation :
Pour la question 5)
-rayon de courbure il faut connaître x et y à t= 2s : R=\sqrt{x^2+y^2

Bonjour phyelec78
Tu es bien sûr de ton coup ? La trajectoire est une parabole, pas un cercle de centre O...
Tu pourrais raisonner sur les propriétés de l'accélération tangentielle et de l'accélération normale. Cela n'est pas très difficile ici car la date t=2s correspond à un cas particulier simple...

Posté par
vanoisere : Cinématique 13-07-25 à 15:03

Ce schéma pourra peut-être aider... Échelle arbitraire pour les normes de vecteurs...

Cinématique

Posté par
Xenoversere : Cinématique 13-07-25 à 16:23

Bonjour Vanoise et phyelec78, pour tout vous dire il y a une correction dont je possède mais dans la correction il y a le raisonnement dephyelec78 et pour être franc, je ne suis pas d'accord avec ça mais plus tôt avec celle de Vanoise qui dit de raisonner sur l'accélération tangentielle et celle centripète car je considère que  phyelec78 ce qu'il a calculé c'est la distance parcouru par le mobile entre l'origine et le sommet du parabole à t=2 secondes et non le rayon de courbure.

Citation :
Bonjour phyelec78
Tu es bien sûr de ton coup ? La trajectoire est une parabole, pas un cercle de centre O...
Tu pourrais raisonner sur les propriétés de l'accélération tangentielle et de l'accélération normale. Cela n'est pas très difficile ici car la date t=2s correspond à un cas particulier simple...
c'est pour ça que j'ai posté l'exercice.

Posté par
vanoisere : Cinématique 13-07-25 à 16:49

Bonjour Xenoverse

Citation :
car je considère que  phyelec78 ce qu'il a calculé c'est la distance parcouru par le mobile entre l'origine et le sommet du parabole à t=2 secondes et non le rayon de courbure.

R2=x2+y2 est l'équation cartésienne d'un cercle de rayon R et de centre O. Rien à voir avec ce problème où la trajectoire est une parabole.
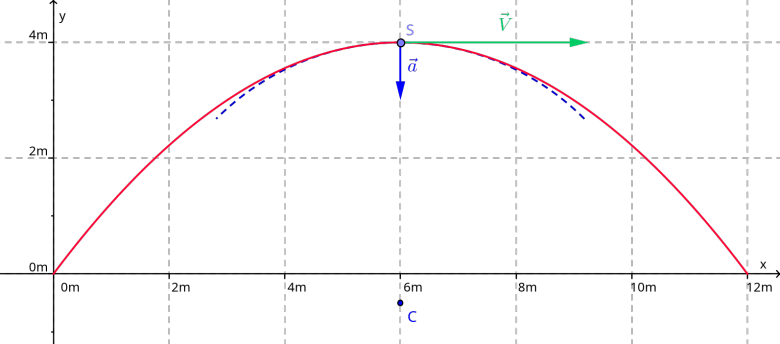
Tu peux remarquer que t=2s correspond au passage au sommet S (voir figure). J'ai représenté à cette date le vecteur vitesse et le vecteur accélération. Que peut-on dire de l'accélération tangentielle ? Que valent dans ces conditions l'accélération normale et la vitesse ? Or la norme de l'accélération normale vérifie :

a_n=\dfrac{v^2}{R}
où R est le rayon de courbure. Tu dois être capable de t'en sortir maintenant...

Posté par
vanoisere : Cinématique 13-07-25 à 16:59

Petit complément : ce quephyelec78 a calculé est la distance en ligne droite de O à S : la longueur du segment (OS) ; rien à voir avec le rayon de courbure de la parabole en S.

Posté par
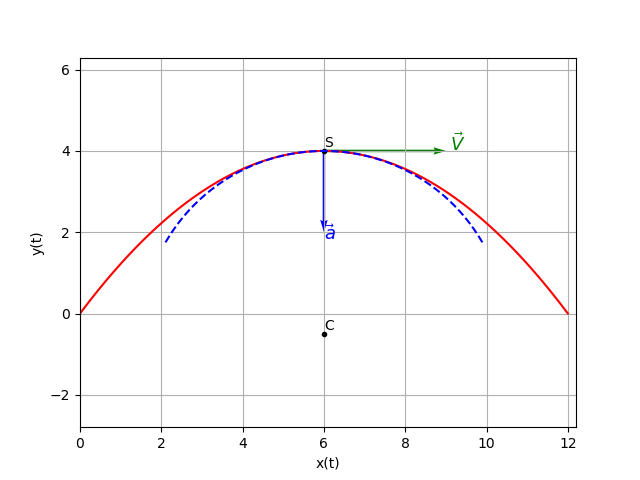
vanoisere : Cinématique 13-07-25 à 17:34

Pour bien illustrer la notion de rayon de courbure R, j'ai tracé en pointillés bleus un arc de cercle de centre C et de rayon CS = R le rayon de courbure. On remarque graphiquement que, au voisinage de S mais seulement au voisinage de S, la parabole se confond pratiquement avec cet arc de cercle.
J'ai utilisé cette fois-ci un repère orthonormé pour mieux visualiser l'arc de cercle.
A toi bien sûr de calculer R par la méthode expliqué dans mon message de 16h49.

Cinématique

Posté par
Xenoversere : Cinématique 13-07-25 à 22:40

Bonjour Vanoise, oui on remarque sur ton graphe que a_t=0 et par déduction a_n=a__totale et pourquoi l'accélération tangentielle serait nulle car je l'ai calculer avec a_t=\frac{v_f-vi}{t_f-t_i} je trouve at=-1m/s² (vi=0; Vf=vs=3m/s;tf=ts=2s et ti=0) puis j'ai cherché a__totale en dérivant le vecteur vitesse V=3i+(-2t+4)j\rightarrow a=-2j \rightarrow||a||= 2m/s2 et avec la formule R_s=\frac{v_s²}{a²-a_t²}je trouve R_s= 3m

Posté par
vanoisere : Cinématique 13-07-25 à 23:19

Un mélange de très bonnes choses et d'erreurs...

Tu as effectivement l'accélération totale : \overrightarrow{a}=-2.\overrightarrow{j}

Il s'agit bien d'un vecteur vertical descendant de norme a=2m/s2

Au sommet S, soit à la date t=2s : \overrightarrow{v}=3.\overrightarrow{i}

Il s'agit bien d'un vecteur horizontal, de norme 3m/s ; résultat cohérent avec un vecteur vitesse tangent à la trajectoire.

Tu sais que le vecteur accélération tangentielle est colinéaire au vecteur vitesse. Ce vecteur ne peut qu'être nul ici, sinon, le vecteur accélération totale ne serait pas perpendiculaire au vecteur vitesse. Ce raisonnement simple est rigoureux et donc suffisant. Tu peux, si cela t'intéresse, retrouver ce résultat par le calcul. Dans le cas général :

a_{t}=|\frac{dv}{dt}|

Attention :il faut raisonner sur la dérivée et non sur le taux de variation de la vitesse, surtout quand celui-ci porte sur une durée assez longue. Ici :

v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{3^{2}+\left(4-2t\right)^{2}}=\sqrt{25-16.t+4.t^{2}}

Je te laisse calculer la dérivée de v par rapport à t puis vérifier que cette dérivée s'annule pour t=2s.

Pour le rayon de courbure en t=2s :

a_{n}=a=2m/s^{2}\qquad v=3m/s

R=\frac{v^{2}}{a_{n}}=\frac{9}{2}=4,5m

Posté par
phyelec78re : Cinématique 14-07-25 à 00:03

J'ai peut-être été un peu vite. Je n'ai pas fait l'exercice.En faite comme dans la question 2, on demande l'équation cartésienne de la trajectoire, j'ai pensé qu'on pouvait prendre comme rayon de courbure OM avec M (x,y) à t=2 s. C'est peut-être faut.

Posté par
phyelec78re : Cinématique 14-07-25 à 00:19

Utiliser la formule R=v2/an me paraît préférable. Sorry.

Posté par
vanoisere : Cinématique 14-07-25 à 09:31

Bonjour phyelec78
Le mot "préférable" n'est pas adapté. À t=2s, \sqrt{x^2+y^2} est égal à la distance SO, pas au rayon de courbure...

Posté par
phyelec78re : Cinématique 14-07-25 à 14:27

@Vanoise oui vous avez raison.

Posté par
vanoisere : Cinématique 14-07-25 à 14:48

Pas grave : tout le monde peut se tromper mais il vaut mieux être clair pour les élèves ou étudiants aidés !

Posté par
Xenoversere : Cinématique 14-07-25 à 15:21

vanoise @ 13-07-2025 à 23:19

Un mélange de très bonnes choses et d'erreurs...

Tu as effectivement l'accélération totale : \overrightarrow{a}=-2.\overrightarrow{j}

Il s'agit bien d'un vecteur vertical descendant de norme a=2m/s2

Au sommet S, soit à la date t=2s : \overrightarrow{v}=3.\overrightarrow{i}

Il s'agit bien d'un vecteur horizontal, de norme 3m/s ; résultat cohérent avec un vecteur vitesse tangent à la trajectoire.

Tu sais que le vecteur accélération tangentielle est colinéaire au vecteur vitesse. Ce vecteur ne peut qu'être nul ici, sinon, le vecteur accélération totale ne serait pas perpendiculaire au vecteur vitesse. Ce raisonnement simple est rigoureux et donc suffisant. Tu peux, si cela t'intéresse, retrouver ce résultat par le calcul. Dans le cas général :

a_{t}=|\frac{dv}{dt}|

Attention :il faut raisonner sur la dérivée et non sur le taux de variation de la vitesse, surtout quand celui-ci porte sur une durée assez longue. Ici :

v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{3^{2}+\left(4-2t\right)^{2}}=\sqrt{25-16.t+4.t^{2}}

Je te laisse calculer la dérivée de v par rapport à t puis vérifier que cette dérivée s'annule pour t=2s.

Pour le rayon de courbure en t=2s :

a_{n}=a=2m/s^{2}\qquad v=3m/s

R=\frac{v^{2}}{a_{n}}=\frac{9}{2}=4,5m

Merci je comprends mieux

Posté par
Xenoversere : Cinématique 14-07-25 à 16:38

vanoise @ 13-07-2025 à 17:34

Pour bien illustrer la notion de rayon de courbure R, j'ai tracé en pointillés bleus un arc de cercle de centre C et de rayon CS = R le rayon de courbure. On remarque graphiquement que, au voisinage de S mais seulement au voisinage de S, la parabole se confond pratiquement avec cet arc de cercle.
J'ai utilisé cette fois-ci un repère orthonormé pour mieux visualiser l'arc de cercle.
A toi bien sûr de calculer R par la méthode expliqué dans mon message de 16h49.

Cinématique

PS: comment représenter ce graphe sur GeoGebra Android de même que les vecteur accélération et vitesse

Posté par
vanoisere : Cinématique 14-07-25 à 17:01

Je n'utilise pas la version Android de GeoGebra mais j'imagine qu'il faut procéder comme sur pc. Je te conseille de tracer d'abord la branche de parabole. Je te laisse trouver son équation cartésienne. Ensuite,placer le point S puis les vecteurs à l'aide des différents menus. Personnellement, je suis plus à l'aise avec Python, question d'habitude...

Posté par
Candidere : Cinématique 14-07-25 à 20:08

Bonjour,

J'ai du mal à suivre pour le rayon de courbure en t = 2s

on a :
x = 3y
y = -t²+4t

et \frac{1}{R} = \sqrt{(\frac{d^2x}{dt^2})^2+(\frac{d^2y}{dt^2})^2}

qui donne après calculs simples, pour t = 2s :  R = 1/2

Sauf si je me trompe, mais il semble bien que dans ce lien :

... on a la même réponse que la mienne pour la valeur de R.

Posté par
vanoisere : Cinématique 14-07-25 à 21:04

Citation :
\frac{1}{R} = \sqrt{(\frac{d^2x}{dt^2})^2+(\frac{d^2y}{dt^2})^2}

C'est moi qui ai du mal à suivre... Ainsi l'inverse d'une distance serait homogène à une accélération... et même ici à l'accélération qui, comme indiqué par l'énoncé, vaut 2m/s2... Pas besoin de faire de calcul pour aboutir à R=1/2 mais cette valeur désigne l'inverse d'une accélération, pas une distance !
D'autre part, la figure postée le  14-07-25 à 16:38 est assez explicite : on y voit bien que, au voisinage de S, la parabole se confond pratiquement avec l'arc de cercle de centre C(6,-0,5) et de rayon R=SC=4,5m.
La méthode que j'ai utilisée semble la seule rigoureuse tout en étant compréhensible au niveau terminale. On trouve d'autres méthodes démontrables au delà du bac et conduisant, elles, à des formules homogènes !

Posté par
vanoisere : Cinématique 14-07-25 à 23:46

On peut illustrer par le calcul la notion de rayon de courbure de la parabole en S de façon assez simple ; il faut tout de même connaître les développement limités à l'ordre 2 d'un sinus et d'un cosinus. Peut-être un peu limite au niveau terminale...

L'équation de la parabole définie précédemment est :

y=-\frac{x^{2}}{9}+\frac{4x}{3}

Je réécris cette équation dans le repère (S,x,y), ce qui conduit à effectuer un changement de coordonnées :

X=x-6\qquad;\qquad Y=y-4

En substituant on obtient l'équation cartésienne dans le repère d'origine S :

Y=-\frac{X^{2}}{9}

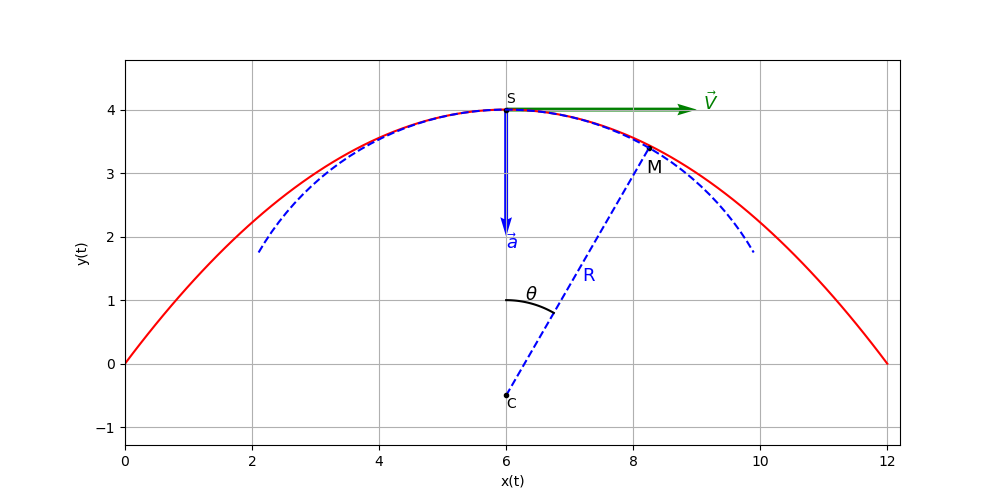
Imaginons maintenant un point C quelconque sur l'axe (S,Y) avec YC<0. Comment choisir la distance R=SC pour que l'arc de cercle de centre C et de rayon R coïncide au mieux avec la parabole au voisinage de son sommet ?

Un point M de cet arc de cercle, repéré par la valeur de l'angle (voir figure) a pour coordonnées :

X_{M}=R.\sin\left(\theta\right)\qquad;\qquad Y_{M}=-R.\left(1-\cos\left(\theta\right)\right)

Supposons maintenant M suffisamment près de S, donc || suffisamment petit pour qu'un développement limité au second ordre soit possible :

X_{M}\approx R.\theta\qquad;\qquad Y_{M}\approx-R\cdot\frac{\theta^{2}}{2} \\
soit :

Y_{M}\approx-\frac{X_{M}^{2}}{2R}

En comparant à l'équation cartésienne de la parabole, on constate que pour || petit, donc au voisinage de S, l'arc de cercle et la parabole sont quasiment confondus à condition que 2R=9m soit R=4,5m.

On retrouve heureusement le résultat déduit de l'expression de l'accélération normale mais la méthode est beaucoup plus longue. La méthode de l'accélération normale est couramment employée au niveau bac+1. Deux exemples :
un grand classique : le mouvement hélicoïdal : Mouvement hélicoïdal - cinématique
autres exemples :

Cinématique

Posté par
phyelec78re : Cinématique 15-07-25 à 00:29

Sauf erreur de ma part à t=2s on se trouve au sommet de la parabole et  1/2a est le rayon de courbure de la parabole en son sommet.
ici a=1/9. Je suis donc du même avis que Vanoise.

Posté par
phyelec78re : Cinématique 15-07-25 à 01:10

Encore un mot :

Sauf erreur de ma part le rayon de courbure d'une parabole est :


R=\dfrac{(1+(\dfrac{dy}{dx})^2)^{\dfrac32}} {\left|\dfrac{d^2y}{d^2x} \right|}

\dfrac{dy}{dx}=\dfrac{-2x}{9}+\dfrac43

x=6 m donc  \dfrac{dy}{dx}=0

\dfrac{d^2y}{d^2x}=\dfrac{-2}{9}

donc

R=\dfrac92=4,5  m

Donc je suis toujours du même avis que Vanoise.

Posté par
vanoisere : Cinématique 15-07-25 à 01:52

Merci phyelec78. Ton message de 0h29 généralise au sommet d'une parabole quelconque le résultat que j'ai démontré pour cette parabole particulière. Ton dernier message est intéressant surtout pour un calcul de rayon de courbure ailleurs qu'au sommet car ce calcul est alors un peu plus rapide que celui utilisant l'accélération normale.
Au moins,que Xenoverse retienne de ces derniers messages : toujours vérifier l'homogénéité d'une formule avant de la valider.

Posté par
Candidere : Cinématique 15-07-25 à 09:54

Bonjour,

Oui erreur de ma part.  

En utilisant le plus classique R = |1 + (f'(x))²|^(3/2) / |f''(x)|

on trouve à partir de f(x) = -x²/9 + 4x/3 que R =  (9/2) * |4x²/81 - 16x/27 + 25/9|^(3/2)

Pour t = 2 s, x = 6 et alors R = (9/2) * |4*36/81 - 16*6/27 + 25/9|^(3/2) = 9/2 * |1|^(3/2) = 9/2 (m)

Posté par
Xenoversere : Cinématique 15-07-25 à 17:15

Bonjour je crois qu'il a une incohérence dans la question 6 de l'exo je m'explique on nous dit qu'un mobile M2 se déplace sur OX à t=0 et x=20m donc vous êtes d'accord que le mobile provient vers la droite et va vers la gauche car on nous demande de calculer l'accélération pour qu'il rejoigne M1 à x= 12 m au point P mais son vecteur vitesse v=2i il doit avoir un signe moins devant

Cinématique

Posté par
vanoisere : Cinématique 15-07-25 à 17:30

Pour la dernière question, tu peux commencer par écrire l'équation horaire sous la forme générale :
xp=(1/2)a.t2+vot+xo
L'énoncé fournit les valeurs de vo et xo
Pour obtenir a, il suffit de poser xp=12m pour t=4s...
Sinon, on peut effectivement tracer la courbe à l'aide de GeoGebra. Le résultat est de bonne qualité. Astuce éventuelle : en cas d'hésitation sur la méthode, poser la question à "Gémini" (intelligence artificielle)...

Cinématique

Posté par
gts2re : Cinématique 15-07-25 à 17:43

Bonjour,

Juste une remarque sur le lien de Candide (14-07-25 à 20:08)

Gauth IA raconte la plupart du temps des âneries en  physique (sauf cas trivial).

Posté par
vanoisere : Cinématique 15-07-25 à 19:29

D'accord avec gts2 : l'IA n'est pas vraiment performante, pour l'instant, en sciences. En revanche, elle peut être de bon conseil sur les programmes informatiques simples...

Citation :
vitesse v=2i il doit avoir un signe moins devant

Pas nécessairement : on peut imaginer une première étape correspondant à un mouvement uniformément retardé vers la droite suivie d'une seconde étape correspondant à un mouvement uniformément accéléré vers la gauche. Je te laisse vérifier que cela est compatible avec une accélération négative (vecteur accélération orienté dans le sens négatif).

Posté par
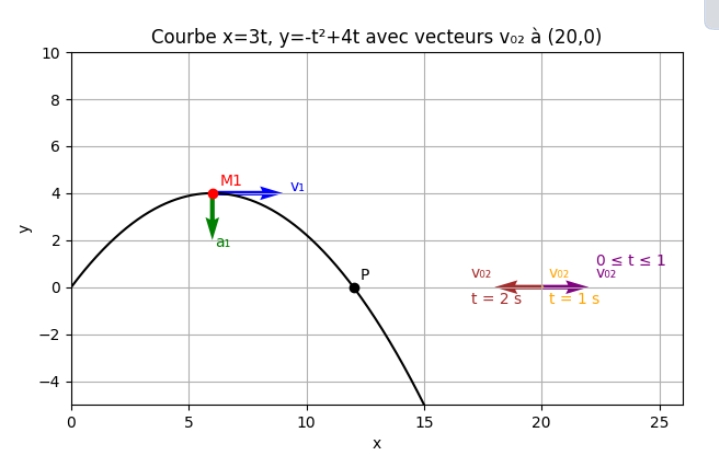
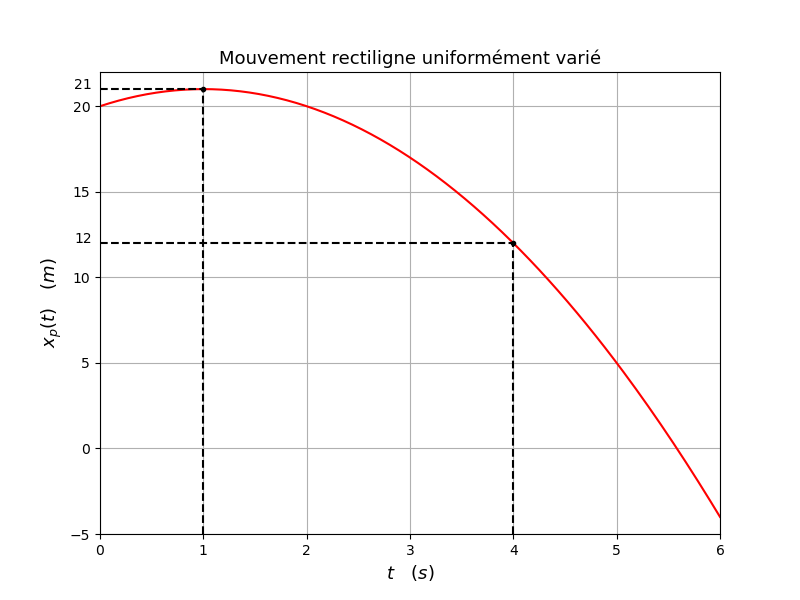
vanoisere : Cinématique 15-07-25 à 21:52

Pour j'espère t'aider à mieux comprendre mon précédent message, voici la courbe représentant les variations en fonction du temps de l'abscisse xp du mobile M2.
Entre t=0 et t=1s, xp augmente de 20 à 21m  et la vitesse diminue (le coefficient directeur de la tangente à la courbe v=dxp/dt diminue), le mouvement est uniformément retardé.
La vitesse s'annule en t=1s (tangente horizontale à la courbe) puis, pour t>1s, xp diminue : le déplacement s'effectue maintenant dans le sens négatif. Le coefficient directeur de la tangente à la courbe est négatif mais de valeur absolue croissante. Le mouvement est uniformément accéléré dans le sens négatif. On vérifie bien que, à la date t=4s, xp=12m. Or l'étude du mouvement du point M1 à montré que celui-ci passe en x=12m à la date t=4s...
Je te laisse calculer l'accélération du mouvement par la méthode décrite dans le précédent message.

Cinématique

Posté par
Xenoversere : Cinématique 15-07-25 à 23:19

Oh que si je comprends mieux ,ta façon d'animer le graphe me plaît mais ici c'est toi qui a supposé qu'il a un déplacement en deux temps (MRU deceleré puis MRU accélération) car l'exercice ne précise pas un truc dans ce genre et dans ce cas il faudrait deux équations horaires une pour MRUD et l'autre pour le MRUA
Bon j'ai calculer l'accélération je trouve a= -2 m/s² mais je l'ai calculer avant de voir ton message et j'ai représenter le vecteur v_02= 2i .
Ps: Vous pouvez me suggérer comment je pourrais apprendre la programmation python pour des tracé des cours...bref pour la géométrie en général bien sûr dans mon téléphone.

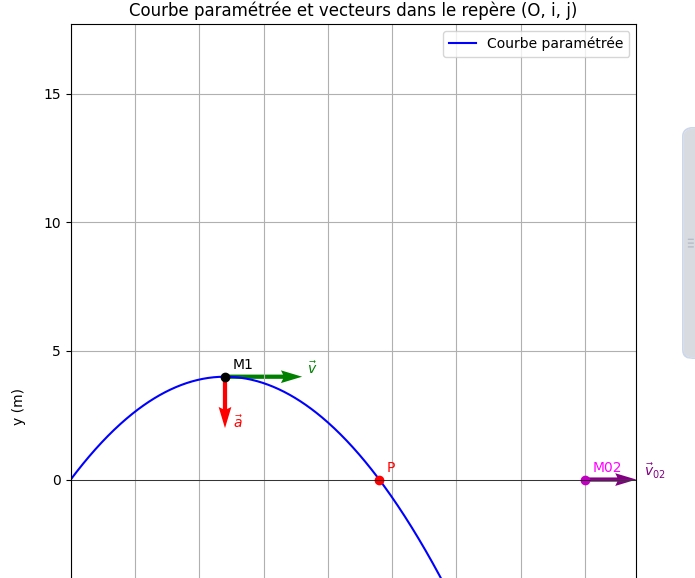
Cinématique

Posté par
Xenoversere : Cinématique 15-07-25 à 23:19

Bon j'ai utilisé l'IA et j'avoue que j'ai bien galéré.

Posté par
vanoisere : Cinématique 16-07-25 à 14:13

Citation :
car l'exercice ne précise pas un truc dans ce genre et dans ce cas il faudrait deux équations horaires une pour MRUD et l'autre pour le MRUA

L'énoncé parle d'un mouvement rectiligne uniformément varié, c'est à dire d'un mouvement rectiligne dont l'accélération reste constante. Comme la vitesse change de sens, cela correspond à deux phases :
phase telle que v.a<0 : mouvement uniformément retardé ;
phase telle que v.a>0 : mouvement uniformément accéléré.
Tant que l'accélération ne change pas, on peut parler d'un mouvement uniformément varié régi par un système unique d'équations. Puisque ici : v=-2t+2, le sens du vecteur vitesse change à la date t=1s mais l'expression de v en fonction de t et l'expression de xp en fonction de t sont les mêmes pour les deux phases.
Tu peux faire une analogie avec le mouvement d'une bille lancée verticalement vers le haut par une personne immobile par rapport à la terre. En négligeant l'action de l'air par rapport au poids, tu obtiens un mouvement rectiligne vertical uniformément varié d'accélération \vec a=\vec g régi par un système unique d'équations et pourtant ce mouvement peut se décomposer en deux phases : une phase ascendante uniformément retardée et une phase descendante uniformément accélérée.

Posté par
vanoisere : Cinématique 16-07-25 à 15:08

Bravo pour ta courbe sous GeoGebra ! Ce n'est effectivement pas évident quand on commence ! Il te faudrait juste apprendre à recadrer la figure pour limiter les ordonnées à [0,5] (en mètres)
Concernant Python, ce n'est pas simple au début mais il s'agit d'un environnement très riche utilisé dans de très nombreux contextes. Pour commencer il te faut télécharger un interface de travail (IDE) qui te permettra de taper ton programme et qui gérera les fenêtres graphiques. Le plus simple à mon avis est THONNY, très facile à télécharger. Ensuite il te faut télécharger les librairies utiles en physiques. Aller dans le menu "outils/Gérer les paquets" et télécharger les paquets les plus utiles : numpy, scipy, matplotlib...
Je te propose à titre d'exemple, le petit programme permettant de charger la courbe précédente : Les textes précédés du symbole "#" ne font pas partie du programme ; ce sont des commentaires utiles à sa compréhension.

pdf
PDF - 14 Ko

Posté par
Xenoversere : Cinématique 16-07-25 à 17:37

OK merci je schematise.

Cinématique

Posté par
Xenoversere : Cinématique 16-07-25 à 17:40

Mais je suis toujours pas convaincu qu'il y a qu'un seul équation horaire pour le mouvement rectiligne uniformément décélérer puis accélérer ,pouvez-vous me montrer comment

Posté par
vanoisere : Cinématique 16-07-25 à 22:20

Le titre de ton dernier schéma m'intrigue. Ce que tu as tracé et tous mes schémas sauf le dernier représentent la trajectoire de M1 soit la courbe y=f(x). La trajectoire de M2 est la demie droite y=0 telle que x21m.
Ma dernière courbe représente les variations de l'abscisse de M2 en fonction de t.
Pour M2 :
V=a.t+vo=-2t+2.
L'accélération et la vitesse initiale étant des constantes, l'expression de V reste la même pour tout le mouvement. Simplement, le signe de v change donc le sens du vecteur vitesse change.
Même chose pour l'équation horaire

x=(1/2)a.t2+vo.t+xo
reste valide tant que l'accélération reste fixe. D'ailleurs le tracé de la courbe x=f(t) permet de décrire la totalité du mouvement. Ce que j'ai fait dans mon message du 15/07 à 21h52.

Posté par
Xenoversere : Cinématique 17-07-25 à 00:02

Bonjour, oui le titre c'est un peu bizarre j'ai même pas remarqué, comme je l'avais dit plus haut je me suis servi de l'IA pour concevoir la programmation c'est pour cela que tout est sens dessus dessous et pour finir ca m'a pris beaucoup de temps.
Bon, j'avoue que je ne comprends toujours pas pourquoi on a qu'un seul équation horaire de x(t) et v(t) même après votre explication mais pas grave de toute façon l'exercice est terminé mais pour info je suis entrain de traiter un exercice qui soulève le même problème à savoir un mouvement rectiligne uniformément varié à deux phases (accélération et décélération) comme notre cas donc si vous êtes disponible soyez prêt car si je finis bon je suis optimiste je vais essayer d'abord de ne pas me planter puis je vais le poster dans un nouveau sujet.merci

Posté par
gts2re : Cinématique 17-07-25 à 07:10

Bonjour,

Pour ce qui est du titre de la courbe, c'est la représentation paramétrique de y(x).

Posté par
vanoisere : Cinématique 17-07-25 à 10:18

Citation :
Pour ce qui est du titre de la courbe, c'est la représentation paramétrique de y(x).

Merci gts2 pour ta sollicitude mais cela : je l'avais compris ! Je me suis juste demandé si Xenoverse faisait bien toujours la différence entre les trajectoires et les représentations graphiques des variations de x en fonction de t...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 244 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !