NB: Mais le problème c'est que comme tu disais ou peut être l'autre qui était intervenue il y effectivement des données redondantes notamment dans le schéma.

Peut être qu'on a coupé l'exercice.

Bonjour,

Explications sur ce qui m'a fait dire que le problème avait des données redondantes mais incompatibles ...

Pour la vitesse entre t = 20 et t = 35 s, on trouve :  

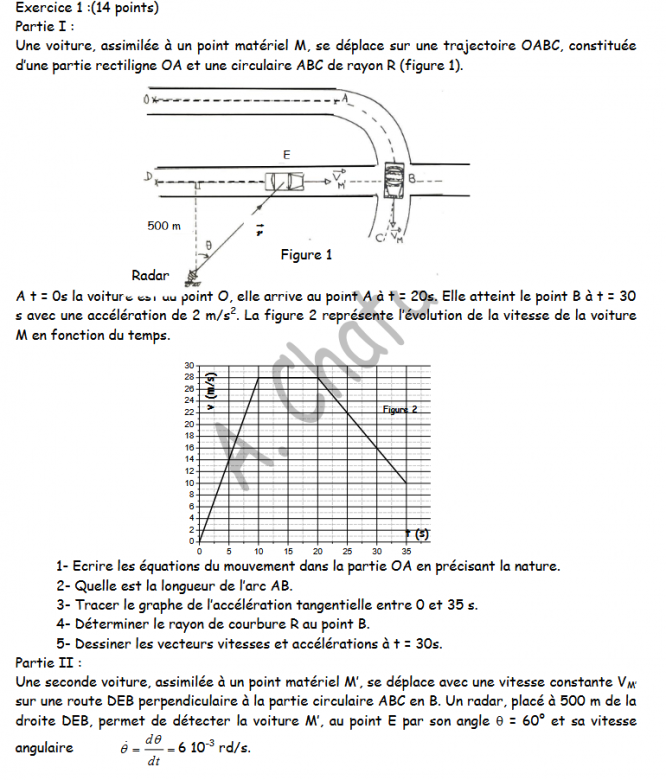
v(t) = 28 - 1,2 *(t-20)
v(t) = 52 - 1,2 t  (avec t dans [20 ; 35 s])

Au point B, on V(B) = 52 - 1,2*30 = 16 m/s (qui correspond bien au graphique)

L'accélération tangentielle en B est |a_T| = 1,2 m/s
L'accélération centripète en B est |a_C| = (vB)²/R = 16²/R = 256/R

L'accélération totale est a = sqrt(1,2² + (256/R)²)

Si on utilise la donnée aB = 2 m/s², il vient donc : sqrt(1,2² + (256/R)²)  = 2
qui aboutit sur R = 160 m

MAIS ... avec les données du problème, on peut calculer autrement, en effet :

L'énoncé précise que "ABC est circulaire de rayon R "

Avec la vitesse tangentielle sur cette portion valant : 52 - 1,2.t
On peut calculer la longueur de l'arc AB, qui est (voir dessin) 1/4 de la circonférence du cercle de rayon R.




  


Mais aussi = arc(AB) = Pi*R/2 (1/4 de la circonférence du cercle de rayon R.)

Et donc Pi*R/2 = 220, qui donn :

R = 140 m (donc différent de ce qui a été trouvé en utilisant a(B) = 2 m/s²

Avec R = 140 m, on aurait a(B) = sqrt(1,2² + 16²/140) = 1,81 m/s² (arrondi) ... donc différent de 2 m/s²

Il y a des données redondantes, puisque tout peut être calculé sans utiliser la donnée de l'accélération au point B.

Mais si on veut , pour faciliter les calculs, donner quand même cette accélération, il FAUT que la valeur donnée soit telle qu'on retrouve la même valeur de R que celle trouvée par les autres données (soit 140 m) ...
et ce n'est pas le cas.

On a donc des données redondantes mais incompatibles ... ce qui rend ce problème bancal.

Sauf si je me suis trompé, mais alors il faudrait me montrer où .  

😂 👍 ok je comprends mieux pourquoi vous dites '' donné redondantes et incompatibles'' , mais je voudrais savoir d'où vient cette équation horaires v(t) = 52 - 1,2 t  (avec t dans [20 ; 35 s])
, moi j'ai travaillé avec v(t) = 28 - 1,2 *(t-20) est-ce que tu as essayé de calculer arcAB en calculant l'intégrale de cette équation de la vitesse dont j'ai utilisé
Mais pour tout te dire  je ne suis pas passé par une intégration mais j'ai juste remplacer avec l'équation de la position remplacer a t=30 secondes qui correspond au point B pour trouver l'arcAB mais aussi peut-être que tu n'as pas fait d'erreur il y a bel et bien des données redondantes et incompatible  je n'ai pas d'expérience là-dessus parce que tout simplement je n'ai pas l'habitude de faire deux chemins dans un même exercice mais peut-être que c'est rare de croiser un tel exercice avec des données incompatibles Mais aussi comment tu as fait cette déduction à savoir arc(AB) = Pi*R/2 (1/4 de la circonférence du cercle de rayon R.)

@candide

Bonjour,

Voir ici :  



Exercice 14

Là, l'exercice est complété par une partie II

Dans lequel, il est écrit :

Partie II :
Une seconde voiture, assimilée à un point matériel M', se déplace avec une vitesse constante VM'
sur une route DEB perpendiculaire à la partie circulaire ABC en B

Comme cette route est dessinée parallèle au tronçon AB et vu les positions de A et B clairement indiquées sur ce dessin (non surchargé), AB est forcément 1/4 de circonférence.

Il n'est pas écrit évidemment que OA et DB sont parallèles, mais le dessin est clair.

Mais chacun pense ce qu'il veut.

Merci pour cet éclairage que je n'avais pas. Effectivement des données sont redondantes et incompatibles