Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Cinématique

Posté par
Samsco 27-03-20 à 19:00

Bonsoir tlm besoin de votre aide svp

Exercice

La position d'un mobile M dans le repère (O,\vec{i},\vec{j},\vec{k}) est donné à chaque instant par le vecteur position \vec{OM} tel que : \vec{OM}=(t²+4t)\vec{i}+(t²+2)\vec{j} avec t>0
1-Montrer que le mouvement est plan et préciser le plan du mouvement.
2-Detrrminer l'équation cartésienne de la trajectoire.
3-Donner l'allure du mouvement

1-La coordonnées cartésienne z(t) du mobile M est nulle donc le mouvement est plan
\vec{v}(v_x(t)=2t+4  ;  v_y(t)=2t) \\ \vec{a}(a_x=2 ; a_y=2) \\ \vec{a}.\vec{v} \\         =x''x'+y''y' \\         = 2(4t+4) \\ \vec{a}.\vec{v}= 8t+8 \\ t>0  \text{donc}  8t+8>0
Le mouvement du mobile M est rectiligne accéléré
2- x=t²+4t
Je ne sais comment exprimer "t" seulement en fonction de x

Posté par
Samscore : Cinématique 27-03-20 à 19:11

Posté par
vanoisere : Cinématique 27-03-20 à 19:53

Bonsoir
Le mouvement n'est pas rectiligne puisque x et y varient en fonction de t. Il faut exprimer x en fonction de t et y en fonction de t.
Ensuite, éliminer t entre x et y pour obtenir l'équation de la trajectoire.

Posté par
Samscore : Cinématique 27-03-20 à 20:29

Donc comment je réponds à la question 1

2-
x=t²+4t \iff t²=x-4t (1) \\ y=t²+2\iff t²=y-2 (2) \\ (1)=(2)\iff x-4t=2-y \iff y=-x+4t+2
Je ne vois pas comment éliminer t

Posté par
Samscore : Cinématique 27-03-20 à 20:32

1- pour la question 1
a est constante donc le mouvement est uniformément varié

Posté par
vanoisere : Cinématique 27-03-20 à 20:54

Pour la question 1 : il suffit de remarquer que z=0 quel que soit t. mais tu as déjà répondu !
D'accord avec tes expressions de x et de y en fonction de t.

Puisque : t>0 :y>2

t^{2}=y-2\quad;donc\quad t=\sqrt{y-2}

La solution mathématique : t=-\sqrt{y-2} n'a pas de sens physique puisque t>0;

4t=x-t^{2}

4\sqrt{y-2}=x-\left(y-2\right)

Tu n'as plus qu'à élever au carré pour avoir quelque chose de plus simple.

Posté par
Samscore : Cinématique 27-03-20 à 21:35


4t=x-t^{2}

4\sqrt{y-2}=x-\left(y-2\right) \\ 16(y-2)=(x-(y-2))² \\ y-2=\dfrac{(x-(y-2))²}{16} \\ y=\dfrac{(x-(y-2)²)+32}{4²}

Posté par
Samscore : Cinématique 27-03-20 à 21:37

Je rectifie quelque chose
4t=x-t^{2}

4\sqrt{y-2}=x-\left(y-2\right) \\ 16(y-2)=(x-(y-2))² \\ y-2=\dfrac{(x-(y-2))²}{16} \\ y=\dfrac{(x-(y-2))²+32}{4²}

Posté par
vanoisere : Cinématique 27-03-20 à 21:44

Cela se simplifie un peu en développant le carré.

Posté par
Samscore : Cinématique 27-03-20 à 22:15

Je rectifie quelque chose
4t=x-t^{2}

4\sqrt{y-2}=x-\left(y-2\right) \\ \\ 16(y-2)=(x-(y-2))² \\ \\ y-2=\dfrac{(x-(y-2))²}{16} \\ \\ y=\dfrac{(x-(y-2))²+32}{4²} \\ \\ y=\dfrac{(x-(y²+4y+4)+32)}{4²} \\ \\ 16y=x-y²+4y+3 \\ \\ y²+12y=x+3

Posté par
Samscore : Cinématique 27-03-20 à 22:22


4t=x-t^{2}

4\sqrt{y-2}=x-\left(y-2\right) \\ \\ 16(y-2)=(x-(y-2))² \\ \\ y-2=\dfrac{(x-(y-2))²}{16} \\ \\ y=\dfrac{(x-(y-2))²+32}{4²} \\ \\ y=\dfrac{(x-(y²-4y+4)+32)}{4²} \\ \\ 16y=x-y²+4y+28 \\ \\ y²+12y=x+28

Posté par
vanoisere : Cinématique 27-03-20 à 22:24

Revois le calcul du carré.  Il fait apparaître un terme en x2...

Posté par
Samscore : Cinématique 27-03-20 à 22:26

Pour la question 1 ,on demande de montrer que le mouvement est plan et de préciser le plan du mouvement
Le fait que z=0 montre le mouvement est plan mais comment je presice le plan du mouvement ?

Posté par
Samscore : Cinématique 27-03-20 à 22:33

J'ai repris et j'ai trouvé

x²+y-2=2xy+4x+16y+40

Posté par
Samscore : Cinématique 27-03-20 à 22:33

J'ai repris et j'ai trouvé

x²+y²=2xy+4x+16y+40

Posté par
vanoisere : Cinématique 27-03-20 à 23:42

Je crois bien qu'il y a encore une erreur de calcul. Personnellement, j'obtiens :

x^{2}-2x.y+y^{2}+4x-20y+36=0
Cela n'a rien de très simple. Pour avoir l'allure de la trajectoire, tu peux prendre quelques valeurs de t et déterminer les valeurs correspondantes de x et y.
A l'instant de date t=0 : x=0 ; y=2 et vy=0 ; le vecteur vitesse initial est donc horizontal ; or, tu dois savoir que le vecteur vitesse est tangent à la trajectoire. La trajectoire admet donc une tangente horizontale en (0,2).

Cinématique

Posté par
Samscore : Cinématique 28-03-20 à 08:56

Donc
C'est ça l'équation de la trajectoire ?

x²-2xy+y²+4x-20y+36=0

Posté par
Samscore : Cinématique 28-03-20 à 09:06

Et normalement l'équation de la trajectoire permet de donner l'allure de la courbe non?

Posté par
vanoisere : Cinématique 28-03-20 à 11:09

Citation :
Et normalement l'équation de la trajectoire permet de donner l'allure de la courbe non?

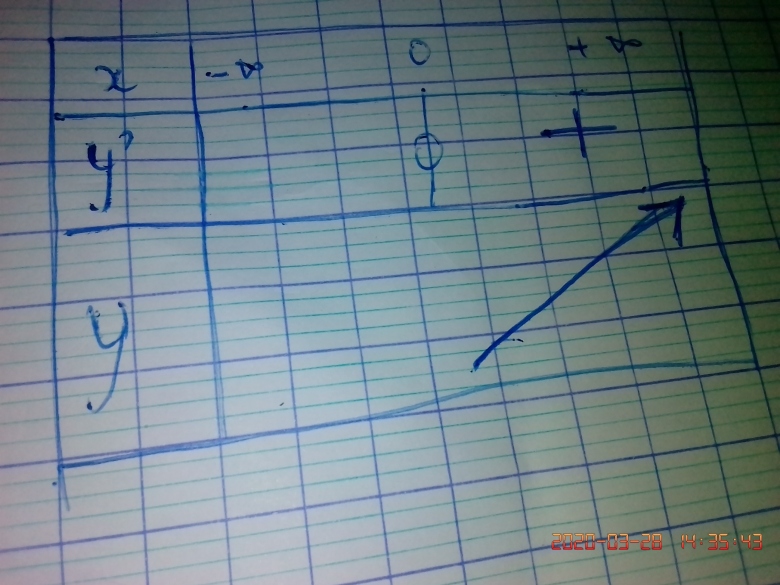
Tu as raison quand il est possible d'écrire l'équation de la trajectoire sous la forme y=f(x). Tu calcules alors la dérivée y'=f'(x), tu remplis un tableau de variations et tu obtiens ainsi l'allure de la trajectoire.
Tu pourrais faire quelque chose d'analogue car, avant d'élever au carré, tu as obtenu :
x=f(y)=y-2+4\sqrt{y-2}
Cela reviendrais à permuter x et y par rapport à ce que tu fais habituellement en maths. Tu peux le faire si tu veux. Comme écrit dans mon précédent message, tu peux aussi d'intéresser aux variations en fonction de t de x, de y et du vecteur vitesse. Fais comme tu préfères en fonction de tes habitudes.

Posté par
Samscore : Cinématique 28-03-20 à 12:31

Pas sûr d'avoir totalement compris ce que vous avez dit mais avec la forme canonique ,j'ai ça:

x=t²+4t \\ x=(t+2)²-4\iff (t+2)²=x+4 \\ t>0 \ \text{donc}  t=\sqrt{x+4}-2 \\ y=(\sqrt{x+4})²+2 \\ y=x-4\sqrt{x+4}+6

Posté par
vanoisere : Cinématique 28-03-20 à 13:01

Ta méthode est tout à fait correcte et sûrement plus en rapport avec tes habitudes de cours de math. Comme tu l'as écrit :

t=\sqrt{x+4}-2

Ensuite, tu as sans doute mal recopié ton avant-dernière ligne avec l'éditeur d'équation car ton résultat est bon :

y=t^{2}-2=\left(\sqrt{x+4}-2\right)^{2}-2=x+4+4-4\sqrt{x+4}-2=x-4\sqrt{x+4}+6

Tu peux éventuellement calculer la dérivée, remplir un tableau de variations et tracer l'allure de la trajectoire.

Posté par
Samscore : Cinématique 28-03-20 à 13:17

Je sais pas comment donner le signe de y'

y'=1-\dfrac{4}{2\sqrt{x+4}} \\ y'=0\iff x=0

Posté par
vanoisere : Cinématique 28-03-20 à 13:55

D'accord avec ton calcul de dérivée et avec la valeur de y' en x=0, d'où l'existence d'une tangente horizontale comme je te l'avais fait remarquer en raisonnant sur la vitesse.
Pour le tableau : n'oublie pas que, puisque t0, x0.
Quel est donc le signe de la dérivée pour x0 ?

Posté par
Samscore : Cinématique 28-03-20 à 14:00

x\geq 0\iff -\dfrac{2}{\sqrt{x+4}}\leq 0\iff y'\leq 1

Posté par
vanoisere : Cinématique 28-03-20 à 14:06

Ce qui compte ici est de savoir si y' est positif ou négatif pour x>0 ; c'est du signe de la dérivée que dépend le caractère croissant ou décroissant de f telle que y=f(x).

Posté par
Samscore : Cinématique 28-03-20 à 14:34

Oui mais comment savoir si y'>0 ou y'<0

Posté par
vanoisere : Cinématique 28-03-20 à 14:46

La dérivée peut s'écrire sous la forme :

y'=\dfrac{\sqrt{x+4}-2}{\sqrt{x+4}}

En remarquant que, pour x>0 : \sqrt{x+4}>2 , tu devrais t'en sortir.

Posté par
Samscore : Cinématique 28-03-20 à 15:34

\sqrt{x+4}-2>0\iff \dfrac{\sqrt{x+4}-2}{\sqrt{x+4}}>0

Posté par
Samscore : Cinématique 28-03-20 à 15:36

Voilà

Cinématique

Posté par
Samscore : Cinématique 28-03-20 à 16:58

La trajectoire est donc une droite ?

Posté par
vanoisere : Cinématique 28-03-20 à 17:58

Non ! On obtiendrait une droite si on avait : f'(x)=constante quel que soit x.
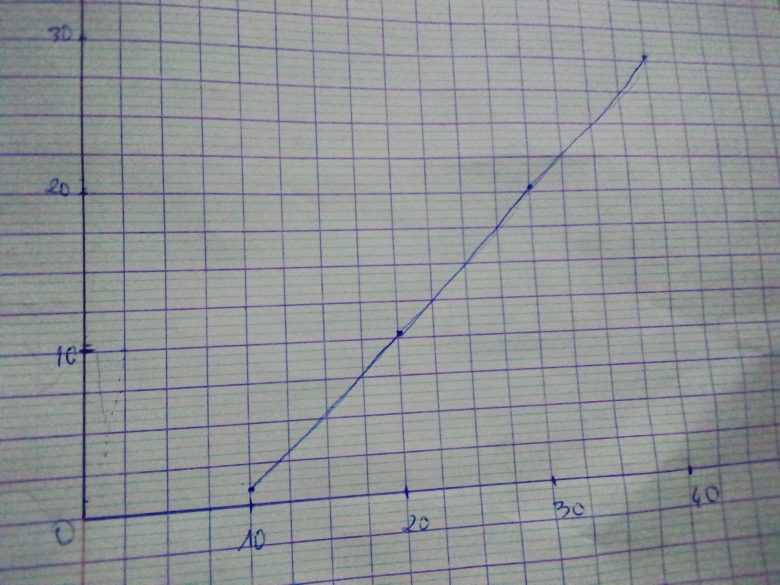
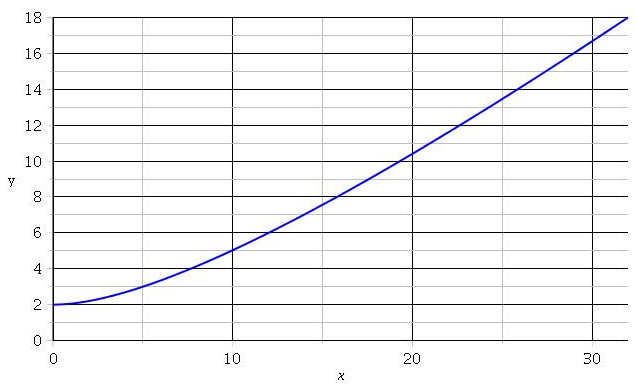
Une dérivée constamment positive sur l'intervalle d'étude signifie que y augmente constamment en fonction de x ; la trajectoire ne présente pas de maximum ou de minimum pour y. Je t'ai fourni hier soir le tracé de la trajectoire réalisé par informatique. Tu peux te contenter de placer dans le repère quelques points, par exemple :
x=0 ; 5 ; 10 ; 15 ; 20 ; 25 ; 30
tu calcules les valeurs de y correspondantes, tu places les points dans un repère puis tu traces l'allure de la courbe à "main levée" sachant que la tangente est horizontale en x=0.

Posté par
Samscore : Cinématique 28-03-20 à 18:08

D'accord je fais et je vous montre

Posté par
Samscore : Cinématique 28-03-20 à 19:01

Voici ce que j'ai fait

Cinématique

Posté par
vanoisere : Cinématique 28-03-20 à 19:39

Regarde bien la courbe que je t'ai fournie ;
Je viens de me rendre compte d'une étourderie dans mon message de 13h01. J'ai mal recopié l'énoncé : y=t2+2 et non t2-2. Désolé !
Heureusement : cela ne modifie pas les messages suivants concernant le raisonnement sur la dérivée mais pour le tracé, il faut rectifier :

\\ y=t^{2}+2=\left(\sqrt{x+4}-2\right)^{2}+2=x+4+4-4\sqrt{x+4}+2=x-4\sqrt{x+4}+10 \\
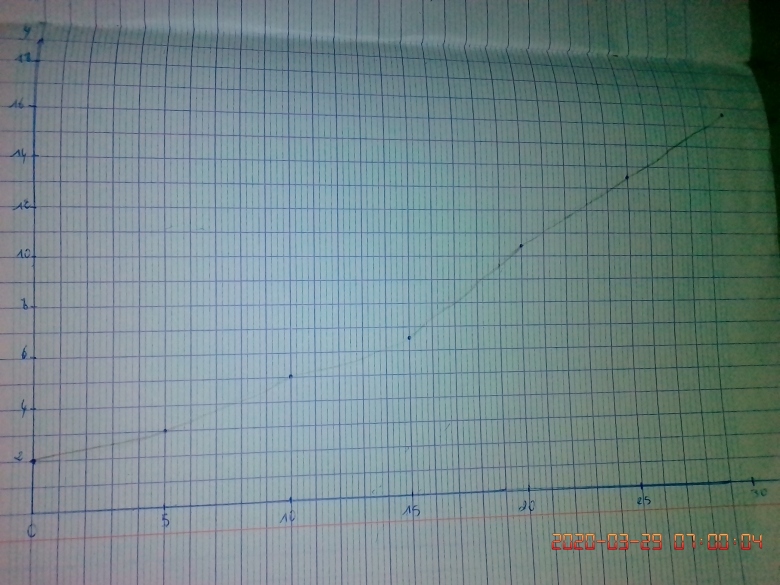
Tu devrais pouvoir t'auto corriger  à partir de la courbe :
y=2 en x=0
y=3 en x=5
....

Posté par
Samscore : Cinématique 28-03-20 à 20:19

D'accord ,je vais refaire

Posté par
Samscore : Cinématique 29-03-20 à 10:45

Voilà

Cinématique

Posté par
vanoisere : Cinématique 29-03-20 à 11:33

Comme déjà écrit : ton tableau de variations ne doit prendre en compte que les valeurs de x telles que : x 0.
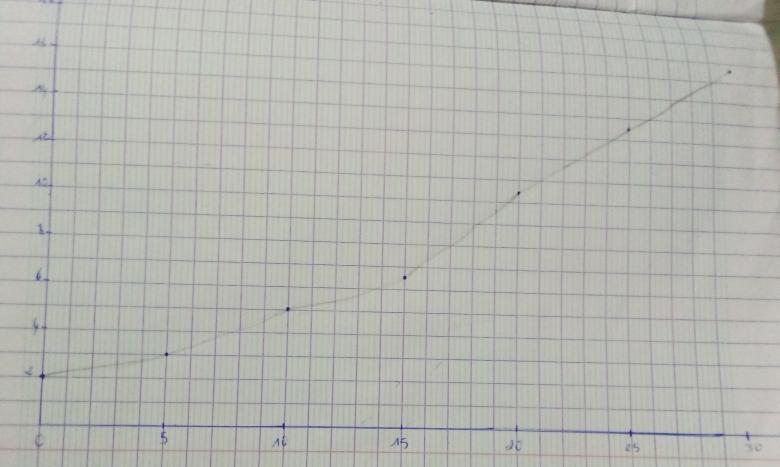
Tu n'as pas posté la courbe mais elle doit être identique à celle que j'ai postée le 27-03-20 à 23:42.

Posté par
Samscore : Cinématique 29-03-20 à 11:36

Je me suis trompé d'image

Cinématique

Posté par
vanoisere : Cinématique 29-03-20 à 12:30

Les points sont correctement placés ; tu peux éventuellement en ajouter d'autres pour une meilleure précision mais attention : la tangente à la courbe en x=0 est horizontale ; cela n'apparaît pas sur ta représentation.

Posté par
Samscore : Cinématique 29-03-20 à 12:30

Est ce que c'est obligé de faire le tableau de variation et la représentation graphique ?

Posté par
Samscore : Cinématique 29-03-20 à 12:32

vanoise @ 29-03-2020 à 12:30

Les points sont correctement placés ; tu peux éventuellement en ajouter d'autres pour une meilleure précision mais attention : la tangente à la courbe en x=0 est horizontale ; cela n'apparaît pas sur ta représentation.

Ok je rectifie au point 0

Posté par
Priamre : Cinématique 29-03-20 à 14:48

Petite erreur pour le point d'abscisse 15.

Posté par
Samscore : Cinématique 29-03-20 à 15:15

Oui c'est vrai f(15)\approx 7,11

Posté par
Samscore : Cinématique 29-03-20 à 15:26

Merci pour tout !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !