Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour, je rencontr un problème dans la résolution d'un exercice en voici l'énoncé :
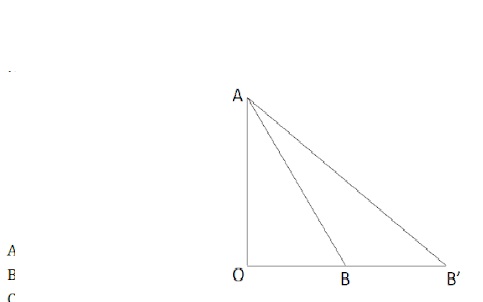
" Deux blocs peuvent glisser sans frottement sur les plans inclinés AB et A'B'(voir image). Lâchés du point A sans vitesses initiale, ils arrivent en B et B' avec des vitesses v et v'. Sachant que OB'=2xOB quelle est la relation entre ces 2vitesses? "
La réponse correcte est v=v'
Voici mon raisonnement :
Il s'agit de deux mouvements rectiligne uniforme.
On suppose x0 et v0 nuls;
D'une part : OB' = a't2 
a'= 2OB'/t2
D'autre part : v= axt or a= 2OB/t2 donc v=2OB/t
v' = a't = 2OB'/t2 x t
Or OB'=2OB donc v'= 4OB/t = 2OB/t x 2 = 2v = v'
Ce qui n'est pas la bonne réponse.
Je ne vois pas là où j'ai fauté dans mon raisonnement, je vous remercie pour toute aide que vous pourriez m'apporter
Bonjour,
Voici mon raisonnement :
Il s'agit de deux mouvements rectiligne uniforme. Non justifié et .... faux !
On suppose x0 et v0 nuls;
D'une part : OB' = a't2 a'= 2OB'/t2 Mais d'où sortent ces relations ? qui sont fausses !
D'autre part : v= axt or a= 2OB/t2 donc v=2OB/t
v' = a't = 2OB'/t2 x t
Or OB'=2OB donc v'= 4OB/t = 2OB/t x 2 = 2v = v'
Conseil :
Mobile 1 :
Pas de frottements. Applique la conservation de l'énergie mécanique entre le point de départ A et le point d'arrivée B. Tire en l'expression V1B de la vitesse acquise au point B
Mobile 2 : Même démarche entre le point A et le point B' . Expression V2B' de la vitesse acquise au point B'
Bonjour odbugt1, j'ai appliqué vos conseils :
Mobile 1 :
Em(A) = Em(B)
mgh = mV1B2 / 2
V1B = 
2gH
Mobile 2 :
Em(A) = Em (B')
mgh = mV2B'2 /2
V2B' = 2gH
On retrouve bien des vitesses identiques. Cependant la relation OB'=2OB n'intervient nul part dans les calculs... est-ce normal?
Remarque :
Tu as attribué la même masse " m " aux deux blocs ce qui n'est pas conforme à l'énoncé.
Il se trouve que la masse disparait au cours du calcul et que cette erreur n'a donc pas de conséquences.
Cela reste un manque de rigueur.
Oui, l'auteur de l'énoncé a tendu un piège avec une donnée inutile. Il aurait pu aussi bien donner OB' = 3, ou 5 ou k*OB cela ne change rien au résultat.
Les deux blocs arrivent en bas avec la même vitesse.
On pourrait montrer que le bloc 2 met davantage de temps pour descendre la pente que le bloc 1 ( Son accélération est plus petite, mais il a une distance plus grande à faire)
D'accord j'ai bien compris.
Pouvais-je aussi dire que v=v' car au point B et B' les vitesses sont nulles?
Et dernière question comment montrer que l'accélération du bloc 2 est plus petite? Faut-il considérer que le bloc 2 est en mouvement rectiligne uniformément accéléré?
Pouvais-je aussi dire que v=v' car au point B et B' les vitesses sont nulles?
Quelle drôle d'idée !
Ces vitesses ne sont pas nulles. Tu as toi même démontré qu'elles étaient égales à
(2gH)
Et dernière question comment montrer que l'accélération du bloc 2 est plus petite? Faut-il considérer que le bloc 2 est en mouvement rectiligne uniformément accéléré?
Les deux blocs ont un mouvement rectiligne uniformément accéléré.
En appliquant la 2e loi de Newton, on motre que dans les deux cas l'accélération est égale à g*sin(
)
est l'angle du plan incliné. Il est plus petit pour le bloc 2 que pour le 1.
Il en résulte que l'accélération g*sin(
) est également plus petite pour le bloc 2
Annuler
connectez vous