Inscription / Connexion Nouveau Sujet
cinématique
bonsoir à tous et toute.
excusez j'ai besoin d'aide pour cet exercice
Une voiture A est arrêtée sur une route horizontale rectiligne à une distance d 1 =3 m d'un feu rouge. Lorsque le feu passe au vert, à l'instant t=0, la voiture démarre avec une accélération constante a 1 =4 m /s 2 . Au même moment un motard M roulant à une vitesse constante v 2 =16 m/s se trouve à une distance d 2 =24 m du feu tricolore. La voiture et le motard considérés comme des points matériels sont repérée à l'instant t à l'aide de leurs vecteurs positions respectifs : (OA) ⃗=x1 i ⃗ et (OM) ⃗=x2 i ⃗. On choisira comme origine O des abscisses la position du feu tricolore.
1° Déterminer les équations horaires x 1 (t) et x 2 (t) de la voiture et du motard respectivement.
2° Déterminer les instants des dépassements ainsi que les positions de la voiture et du motard à ces instants.
3° Si le motard roulait à la vitesse v 2 =11 m/s pourrait-il rattraper la voiture ?
4°
4.1. Calculer, dans ce cas, l'instant pour lequel la distance qui sépare le motard de la voiture est minimale.
4.2. En déduire cette distance.
j'ai fais la première question.
X1= 2t^2+3
V1=4t
et
X2=16t+24
V2=16
aidez moi pour le reste svp!
merci d'avance
Bonjour,
Avant d'aller plus loin, il te faut corriger tes expressions de x1(t) et x2(t) qui sont fausses.
D'après tes expressions :
x1(0) = 3m
x2(0) = 24m
Le schéma ci dessous représente la situation à la date t=0 et il n'est pas en accord avec tes équations.
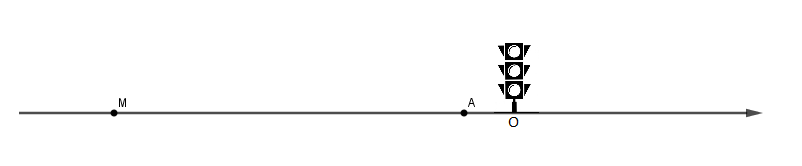
Pas d'accord !
On repère les positions sur un axe orienté dont l'origine coincide avec le feu tricolore.
A la date t=0 l'automobile se trouve 3m avant le feu donc x1(0) = -3m
Et évidemment pour le motard x2(0) = 24m
Les équations horaires correctes sont donc :
x1(t) = 2t² - 3 et
x2(t) = 16t -24
Les dates de dépassement correspondent aux instants ou x1(t) = x[sub][/sub](t)
ouf j'ai oublié le repère.
mais pour les date de dépassement.
Et j'ai du mal à comprendre : x1(t) = x[sub][/sub](t)
merci d'avance
C'est une faute de frappe de ma part.
Je rectifie :
Les dates de dépassement correspondent aux instants ou x1(t) =x2(t)
Les deux mobiles ont la même abscisse aux dates de dépassement.
donc si : x1(t) =x2(t) équivaut à 2t² - 3=16t -24
2t² -16t +21=0
et après je trouve: t1=8−22/2 et t2=8+22/2
donc si : x1(t) =x2(t) équivaut à 2t² - 3=16t -24
2t² -16t +21=0 OK pour cette équation
et après je trouve: t1=8−22/2 et t2=8+22/2 Non
Il est évident que tes résultats sont faux.
Le simple fait qu'ils soient rendus sans unité les qualifient déjà automatiquement comme faux.
De plus, en physique un résultat ne se rend jamais sous forme de fraction (ou de racine).
L'écriture sans parenthèses de t1 ne permet pas de savoir si tu as trouvé t1=(8-22)/2 = -7s ou bien
t1= 8-(22/2) = -3s . Même chose pour t2
La valeur négative de t1 que tu trouves signifierait qu'un dépassement aurait lieu 7s o(u 3s) avant que le feu passe au vert. Evidemment faux !
OK excusez je me suis trompé dans les calculs
t1=(8+√22)/2=25,38s
t2=(8-√22)/2=6,61s
Donc de la je peux en tirer une conclusion
Revois encore ton calcul, je ne trouve pas la même chose :
t1 = 1,65s
t2 = 6,35s
1,65s après le passage du feu au vert, le motard qui est lancé dépasse l'automobile qui vient tout juste de démarrer.
6,35s après le passage du feu au vert, l'automobile dont la vitesse augmente régulièrement dépasse le motard.
Question 3 : C'est le même calcul que pour la question précédente.
L'équation horaire de A n'a pas changé, celle de M doit être modifiée avec la nouvelle valeur de la vitesse.
On recherche pour quelles dates x1(t) =x2(t) et on obtient une équation du 2e degré comme précédemment.
Si cette équation n'a pas de racines cela signifiera qu'il n'existe aucune date pour laquelle x1(t) =x2(t) et donc que le motard ne rattrapera pas la voiture.


