Attention, tu vas te faire "boxer" par un modérateur qui va certainement supprimer ton envoi.

On ne peut envoyer de scan d'exercice sur le site, tu dois recopier ton énoncé.
Seuls les dessins accompagnant peuvent être mis sur le site.

Pour une fois, je mets tes dessins sur le site ...
Il te restera à recopier l'énoncé.

D'accord merci
Donc pour répondre à cette question on a plusieurs documents :

Document 1 : L'expérience de Galilée au XVIIème siècle
« J'ai pris deux boules, l'une de plomb et l'autre de liège, celle-là  au  moins  cent  fois  plus  lourde  que celle-ci, puis j'ai attaché chacune d'elles à deux fils très légers, longs tous les deux de quatre coudées; les écartant alors de la position perpendiculaire, je les lâchais en même temps; une bonne centaine d'allées et venues,  accomplies  par  les  boules  elles-mêmes, m'ont clairement montré qu'entre  la  période  du  corps
pesant et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n'acquiert sur le second aucune avance, fût-ce la plus minime,  mais que tous les deux ont un rythme de mouvement  rigoureusement  identique.
On  observe  également  l'action  du  milieu  qui,  en  gênant  le mouvement,  ralentit  bien  davantage  les  vibrations  du liège  que  celles  du  plomb,  sans  toutefois  modifier
leur fréquence.»

D'après Discours et démonstrations mathématiques concernant deux sciences nouvelles, publié en 1636.


Puis le document 2  : La période propre
On reproduit l'expérience de Galilée en laboratoire avec un pendule composé  d'une  bille  de  plomb  de  masse m=  50 g de  centre d'inertie G, et d'un fil de longueur L accroché  en O.
On choisit la position à l'équilibre G0 de G comme origine des altitudes z. Pour un  amortissement  faible,  la  pseudo-période T du  pendule  est voisine de sa période propre T0. L'expression de la période propre du pendule est :
T= 2L/g

L désigne la longueur du fil du pendule.

Un  système  informatique  permet  d'obtenir  les  mesures de  l'abscisse  x  du  centre  d'inertie  G  du pendule représentées sur le graphe du document 3.

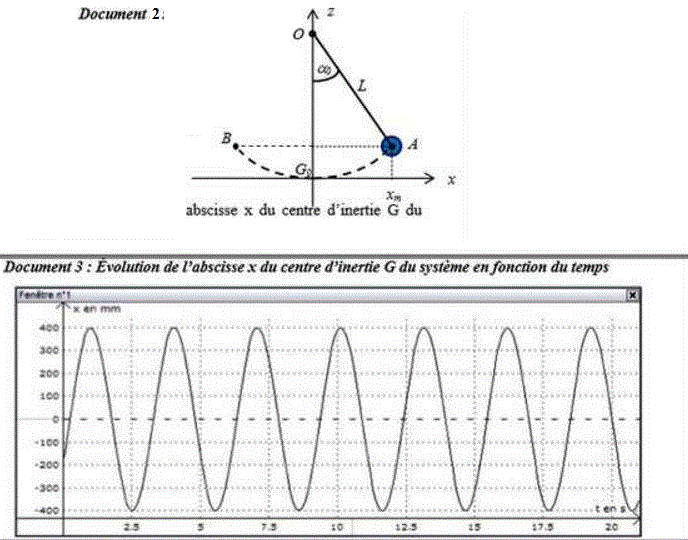
Document 3 : voir le graphique

On a aussi les données suivantes :
Une coudée = 0,573m
L'accélération de pesanteur : g=9,81m.s^-1
Masse du pendule de plomb de Galilée : m=50g

Merci d'avance

L = 4 * 0,573 = 2,292 m (4 coudées)


Soit h, le distance entre A et l'axe des abscisses.

Pythagore : Xm² + (L-h)² = L² (voir sur dessin doc 2)

Or Xm = 0,4 m (amplitude de l'oscillation lue sur diagramme 3)

0,4² + (2,292 - h)² = 2,292²

h = 0,03517 m
-----
On a aussi (voir sur dessin doc 2)

L - h = L cos(alpha0)
h = L(1-cos(alpha0))

0,03517 = 2,292 * (1 - cos(alpha0))
cos(alpha) = 0,98465...

alpha0 = 10° (arrondi)
-----
Recopier sans comprendre est inutile.

Salut à vous deux,

"Boxer" c'est un peu fort, mais rappelé à l'ordre ça c'est clair.

D'accord merci beaucoup pour votre aide. Il faut faire les 2 étapes pour trouver l'angle ?

XM = 0,4
L = 2,292 m

XM = L*sin(alpha0)

sin(alpha0) = 0,4/2,292

alpha0 = 10°

En faite, il y a plusieurs façon d'y arriver,c'est ça ?

La question suivante svp c'est : Pourquoi peut on considérer, à la vu du document 3, que l'énergie mécanique du pendule se conserve ? En déduire la vitesse v de la bille au point G0.
Merci

L'amplitude de l'oscillation varie-t-elle avec le temps ? (voir sur doc 3)

Et donc ...
----
1/2.m.(V(Go))² = mgh (conservation de l'énergie mlécanique)
(V(Go))² = 2gh

(V(Go))² = 2g .L(1-cos(alpha0))
...

-----
Sauf distraction.  

Voila ce que j'avais mis : le pendule oscille librement sans amortissement c-a-d qu'il n'y a  pas de forces de frottements par conséquence la variation de l'énergie mécanique est nulle et donc l'énergie mécanique se conserve.

Est ce que ça va ? svp

C'est juste, mais on te demande de déduire cela à partir du doc3 ...

Et cela se fait en constatant que l'amplitude de l'oscillation ne varie pas avec le temps sur le doc3

Donc si je rajoute :
D'après le doc 3, on peut voir que l'amplitude de l'oscillation de ne varie pas avec le temps donc il n'y a  pas de forces de frottements par conséquence la variation de l'énergie mécanique est nulle et donc l'énergie mécanique se conserve.

c'est mieux ?

Oui

D'accord merci de votre aide, c'est gentil !