1) Ecris les équations d'un mouvement uniformément accéléré :
x = 1/2 at² + vot + xo
v = at + vo .
Au point où commence la décélération, on a  xo = 0  et  vo = 60 km/h .
En éliminant le temps  t  entre ces deux équations, tu pourras calculer l'accélération (négative)  a  durant cette phase du mouvement.

Donc : x=1/2at^2+Vot+xo

x=1/2at^2+60t+0

100=1/2g2^2+2Vo
100=1/2g4^2+Vo
50=2g+Vo
50=2g+60

Suis-je bien partie ?

Salut Yelp !

Pour le 1), la voiture freine, donc son "accélération" tend à la faire ralentir (on parle alors de décélération mais en physique on ne fait pas la différence entre les 2 en général, on utilise toujours le mot accélération !).
Le vecteur accélération est alors opposé à la trajectoire de la voiture !

Pour l'intensité et la durée, je pense que la méthode la plus simple est de faire les 2 en même temps, c'est-à-dire résoudre un système de 2 équations à 2 inconnues obtenu grâce aux équations de base que tu peux écrire.

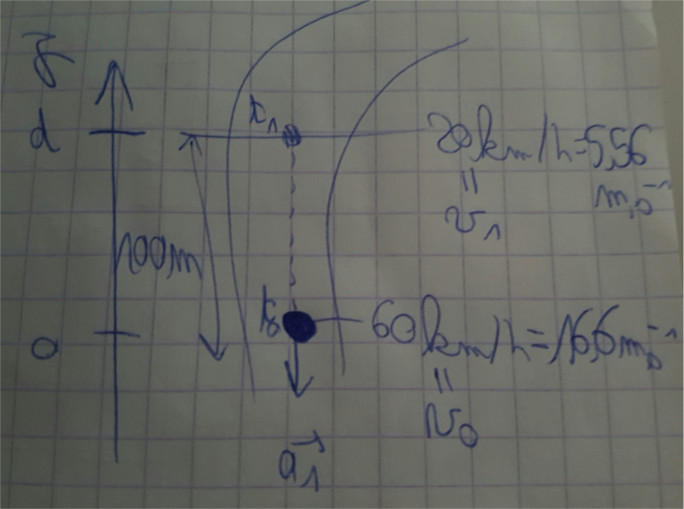
En notant t₁ le temps où il commence le virage (donc le temps où il arrive à 20 km/h) et d la distance entre le début et la fin du freinage (100m) tu peux obtenir 2 équations : 1 portant sur la vitesse de la voiture à t₁ et l'autre portant sur la position de la voiture à t₁ ! Fais un beau schéma pour t'aiguiller.

En résolvant le système tu peux trouver t₁ (qui est la durée de cette phase puisqu'il commence à freiner à t = 0), puis a₁. Attention aux unités ! Passe tout dans les unités SI (m, s, m.s^-1 et m.s^-2).

Ensuite, pour la 3), dis toi que sa vitesse reste constante lors du virage, donc pas d'accélération (mais il existe une accélération centripète (qui pète au centre, donc dirigée vers le centre) dirigée de la voiture vers le centre du cercle de la trajectoire, je ne sais pas si c'est demandé mais elle existe quand même c'est elle qui te donne l'impression d'être projeté vers l'extérieur du virage quand tu tournes en voiture).

Bon j'arrive trop tard mais si ça peut t'aider je laisse... La suite arrive en tout cas.

Petit conseil : ne remplaces les valeurs numériques (Vo, x...) qu'à la toute fin de tes calculs, lors de l'application numérique sur ta calculette ! Comme ça c'est plus clair. Du coup reprends à partir de la 1ère équation qui est bonne.

Un petit schéma vite fait et tout sale mais on comprend l'idée.

Pour la vitesse angulaire je ne sais pas si vous l'avez vue en cours, elle se note et son expression est la suivante, pour un mobile se déplaçant sur un cercle de rayon R, à vitesse V : .

Après pour la durée du parcours circulaire, il se déroule à vitesse constante, du coup on ressort du placard la vieille formule ! On a tout sauf ce que l'on cherche (t) du coup c'est parfait me semble t-il !

Bon courage pour la suite et n'hésite pas si tu  as des questions !

L'image :

Pardon je suis allé trop vite, on a pas d ! Mais il est précisé que le virage fait 180°.
On utilise alors cette formule magique très importante qui donne la longueur d'un arc de cercle de rayon R et d'angle : (où est en radians, ici c'est rad).


Tu remarques que pour on retombe sur la formule du périmètre d'un cercle : !

Bonjour, merci pour votre aide c'est vraiment très gentil
Ce qui me pose problème c'est justement le système pourriez-vous m'éclairer?  

Merci d'avance

Le système est vraiment important en mécanique quand tu veux appliquer le PFD mais ici on est juste en cinématique. Bien sûr cela peut t'aider à comprendre le problème. Ici on a simplement une voiture arrivant à une vitesse initiale à t=0 et soumise à une accélération négative (car elle freine) entre t=0 et t=t₁.

Au vu de ces données on peut grandement simplifier le problème et considérer la voiture comme un point matériel soumis à une accélération a₁ négative... Puis lui appliquer les équations cinématiques :







Puis enfin choisir un point judicieux afin d'utiliser intelligemment ces équations pour résoudre le problème !

A vrai dire j'ai vraiment du mal à visualiser la situation, il faut que j'isole les a1 puisque l'intensité est une accélération ?

Regarde mon schéma, la voiture se déplace selon les pointillés mais elle a une accélération opposée à ce sens ! Cela semble paradoxal mais comme la voiture a déjà une vitesse initiale, cette accélération ne fait que la ralentir !

Ici rien à isoler il n'y a qu'un mobile que l'on peut assimiler à un point c'est beaucoup plus facile.