Inscription / Connexion Nouveau Sujet
cinematique
Bonsoir, pouvez-vous m'aider pour cet exercice j'arrive pas à le démarrer
Une rame de métro pénètre dans un tunnel avec un vecteur vitesse (V0 ). Son mouvement est rectiligne uniformément varié avec le vecteur accélération a. Elle parcourt 30m en 2s, puis 60m en 3s.
1°/ Calculer a et V0.
2°/ Quelle est la distance parcourue ?
3°/ En fin le métro freine. Son mouvement devient rectiligne uniformément retardé jusqu'à l'arrêt avec un vecteur accélération opposé à celui du premier mouvement. Calculer la distance parcourue depuis l'entrée dans le tunnel.
Bonjour,
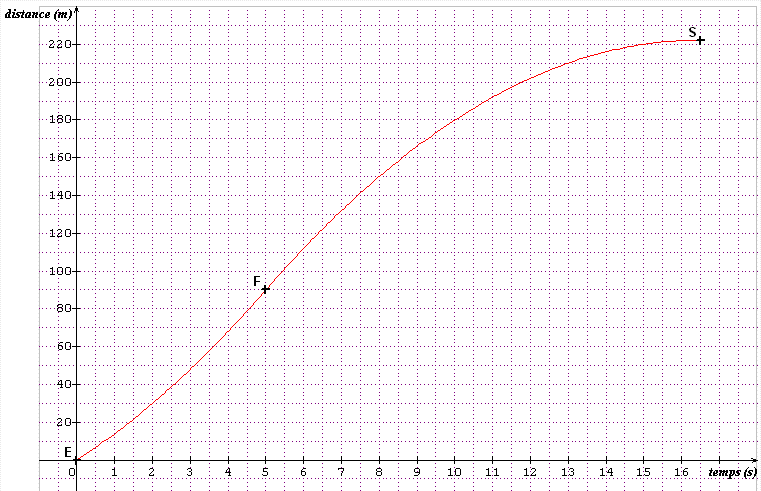
Une image qui traduit l'énoncé ?
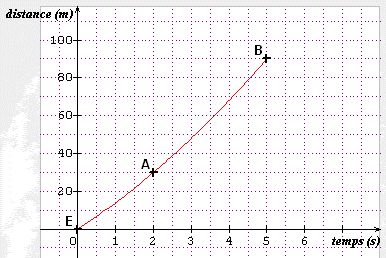
Tu as pour la première question deux inconnues.
Il faudra selon toute probabilité deux équations... et l'énoncé donne les éléments pour les écrire.
Équation horaire...
E est l'entrée du tunnel
A correspond à la première information donnée par l'énoncé
B à la seconde information
À toi !

Merci, voici donc ce que j'ai fait:
x= (1/2) at^2 + V0×t
Pour x=30, t=2 et pour x=90 t=5
On obtient un système d'équation à 2 inconnues : 30=2a + V0
90=(25/2)a + 5V0
j'ai trouvé a=2m/s2 et V0=13m/s
2°/ Pour la distance parcourue c'est 90m:
3°/ Vf^2-V0^2=2ad d'où d= -V0^2/2a donc d=42,25m
D'accord pour les réponses aux questions 1 et 2
Pas du tout d'accord pour la réponse à la question 3
Au moment où il commence à freiner il a déjà parcouru 90 m (réponse à la question 2) depuis l'entrée du tunnel, alors...

Si je comprend après 90m on peu calculer la deuxième distance d parcourue et la vitesse V1 à t=90m
V1=at+V0 V1=2x2+13=23m/s
Vf^2-V1^2=2ad d'où d= -V1^2/2a donc d=123,25
Donc la distance totale est 90+123,25=222,25m