Niveau terminale

Cinématique

Posté par
grievous 15-07-12 à 23:05

Bonjour voici mon ennonce:
Un mobile se déplace dans un repère O,i,j,k à la vitesse V0=i-4j+8k
Il est alors soumis à l'action d'une force F qui lui impose une accélération
a=0,2i+j-0,2k
Calculer la vitesse V acquise au bout de t=10s.
Comparer les vecteurs V0 et V.

Alors moi voilà ce que j'ai fais:
Je sais que v=at+V0
Donc: v = (0,2t+1)+(t-4)+(-0,2t+8)
Comme a V0;t=0
Alors v0=1-4+8=5m.s-1
La correction m'a dite le contraire, voilà ce qu'elle a mise:

Je sais que v=at+V0
Donc: v = (0,2t+1)+(t-4)+(-0,2t+8)
Comme a V0;t=0
Alors v0=1²+4²+8²
V0=9m.s-1

Je ne comprend pas du tout déjà pourquoi chaque nombre est mis au carré puis le tout en racine , et d'autre part pourquoi la correction nous indique +4 alors quelle nous a indiquée -4 un peu plus tôt ... (je l'ai mis en gras pour mieu repérer)

Pouvez vous me répondre de façon assez détaillée et pédagogue ? Merci

Posté par re : Cinématique 16-07-12 à 07:30

Bonjour,
La racine carrée, c'est le module du vecteur V0.
Tous les calculs de v que tu as faits, sont des calculs vectoriels.
Il manque les vecteurs i, j et k.

Posté par re : Cinématique 16-07-12 à 08:14

Bonjour,

La vitesse d'un mobile est représentée en physique par un vecteur.

Écrire que $\vec{V_0}\,=\,\vec{i}-4\vec{j}+8\vec{k}$

C'est une manière d'écrire que le vecteur $\vec{V_0}$ peut être considéré comme la somme de trois composantes, trois vecteurs
$\vec{OA}\,=\,1\times\vec{i}$
$\vec{OB}\,=\,-4\times\vec{j}$
$\vec{OC}\,=\,8\times\vec{k}$

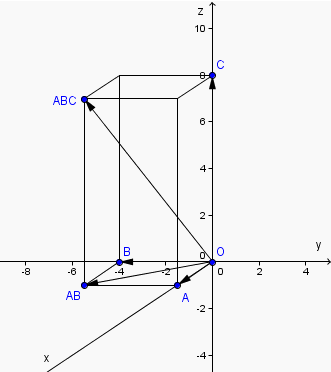
Cinématique

Comment calculer la longueur (la "norme", le "module") du vecteur $\vec{V_0}$ ?
Il faut appliquer à deux reprises le théorème de Pythagore.

La norme du vecteur $\vec{OA}$ vaut 1
La norme du vecteur $\vec{OB}$ vaut 4

(la norme d'un vecteur, sa longueur, est toujours positive)

Appliquons le théorème de Pythagore dans le triangle O A AB, triangle rectangle en A : le carré de l'hypoténuse vaut la somme des carrés des petits côtés, donc
$1^2\,+\,4^2$

Appliquons une deuxième fois le théorème de Pythagore, dans le triangle O AB ABC qui est un triangle rectangle en AB : le carré de l'hypoténuse vaut la somme des carrés des petits côtés, donc
$(1^2\,+\,4^2) \,+\,8^2\,=\,1^2\,+\,4^2\,+\,8^2$

Et le module (la norme, la longueur) du vecteur $\vec{V_0}$ vaut donc :

$||\vec{V_0}||\,=\,\sqrt{1^2\,+\,4^2\,+\,8^2}$

Posté par re : Cinématique 16-07-12 à 08:16

Bonjour sanantonio312

Excuse-moi !
Je constate que certains dessins et certaines explications (reprises plusieurs fois...) sont parfois fort longs à élaborer.

Posté par re : Cinématique 16-07-12 à 12:56

Salut Coll.
Tu es tout pardonné.
Au moins, ta réponse est complète.
Mais sur une tablette, pas facile dessiner.
Espérons que grievous sera content(e)...

Posté par re : Cinématique 16-07-12 à 14:40

Oui je suis content vos explications me permettent de comprendre les secrets de la physique !!
Merci de vous donner tous ce mal!

Posté par re : Cinématique 16-07-12 à 17:03

On connaît la vitesse initiale : $\vec{V_0}\,=\,\vec{i}-4\vec{j}+8\vec{k}$

On connaît l'accélération (qui se représente, en physique, également par un vecteur) : $\vec{a}\,=\,0,2\vec{i}+\vec{j}-0,2\vec{k}$

Quelle est donc la nouvelle vitesse $\vec{V}$ après une application de cette accélération $\vec{a}$ pendant une durée de 10 secondes ?

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cinématique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique