Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Cinématique 2

Posté par
beugg 03-12-16 à 23:37

Bonsoir
J'aurais besoin d'aide pour cet exercice
Un mobile se déplace dans le plan muni d'un repère R (o,i,j) avec un vecteur accélération \vec{a}= -8\vec{j}.À l'instant t=0 ,le vecteur position du mobile ainsi que son vecteur vitesse sont données respectivement par:
\vec{OM}_0=-3\vec{i}+3\vec{j} et
\vec{V}_0=2\vec{i}+4\vec{j}.

1/Montrer que l'équation cartésienne de la trajectoire est de la forme
y= Ax2+Bx+C  
Où A,B et C sont des constantes à déterminer
2/ 0 s t 2,5 s
3/ À quelle date le mobile atteint-il le sommet de la trajectoire ?
4/ Calculer la vitesse moyenne du mobile entre les instants t0=0 s et t1= 1 s. En déduire l'accélération moyenne entre ces mêmes instants.
5/ Calculer les accélérations normale et tangentielle pour t= 0,5 s. Les représenter dans la courbe précédente (prendre 1 cm correspond à 4 m/s )
6 ) Sur quel intervalle de temps le mouvement est décéléré ?

Posté par
beuggre : Cinématique 2 03-12-16 à 23:38

Merci de me guider pour la première question

Posté par
diracre : Cinématique 2 04-12-16 à 08:18

Hello

Je crois me souvenir que les notations "avec des points" ne te posent pas de problème:

Citation :
vecteur accélération \vec{a}= -8\vec{j}


Donc
\forall t \geq 0,
\ddot{x} = 0
\ddot{y} = -8

Ne reste plus qu'à intégrer pour trouver  \dot{x}  et   \dot{y}   (tu connais les conditions initiales)

Puis à nouveau pour trouver  x  et  y

Ensuite l'exercice ressemble à un exercice que tu as traité il y à qlq jours il me semble.    

Posté par
beuggre : Cinématique 2 04-12-16 à 10:38

Hello dirac
Merci d'avoir répondu

Mais avec vec(aV) ,comment peut-on montrer que

y= Ax2+Bx+C ?

Posté par
diracre : Cinématique 2 04-12-16 à 11:00

On va y aller "step by step" alors:

Je considère que tu es d'accord avec ce qui est écrit ci dessous,  car  \vec{a}= 0.\vec{i} +( -8).\vec{j}:

\\ \ddot{x} = 0 \\ \ddot{y} = -8

Peux tu alors calculer  \dot{x}     et   \dot{y}    en fonction de t?

Posté par
beuggre : Cinématique 2 04-12-16 à 11:17

\dot{x}=2t \\ \\ \dot{y}=4t
?

Posté par
beuggre : Cinématique 2 04-12-16 à 11:22

Plutôt

beugg @ 04-12-2016 à 11:17

\dot{x}=2 \\ \\ \dot{y}=4
?

Posté par
diracre : Cinématique 2 04-12-16 à 11:24

Non ...

As tu vu en cours les primitives? les primitives usuelles?

f = 0     primitive    F = Cste

f= a     primitive     F = a.t + Cste

f = a.t   primitive    F = \frac{1}{2}a.t^2 + Cste

La Cste étant donnée par les "conditions initiales" (quand t = 0)

Tu essaies à nouveau?

Posté par
beuggre : Cinématique 2 04-12-16 à 11:50

Non je n'ai pas encore fait les primitives !

x= (1/2).at2+v0t+x0

J'ai une correction qui trouve:
Pour \vec{M}:

x= 2t -3
y= -4t2+4t+3

Mais je ne comprends pas bien

Posté par
diracre : Cinématique 2 04-12-16 à 12:02

Aïe ... je ne vois pas trop comment résoudre ce pbm sans "intégrer" l'accélération pour trouver la vitesse, puis la vitesse pour trouver la position. Sauf à "présupposer" x(t) fonction linéaire de t et y(t) fonction parabolique de t.

Donc

\\ \ddot{x} = 0 \\ \ddot{y} = -8  

Soit, en intégrant sur la variable t:

\\ \dot{x} = Cste1 \\ \dot{y} = -8 t + Cste2

Cste1 et Cste2 sont données par les conditions initiales


\\ \dot{x}(t=0) = Cste1= 2 \\ \dot{y}(t=0) = -8 \times0 + Cste2 =4

Donc  

\\ \dot{x} = 2 \\ \ddot{y} = -8 t + 4      soit      \vec{V} = 2.\vec{i}  + (4-8t).\vec{j}

Arrivés là  on est bon?

Posté par
beuggre : Cinématique 2 04-12-16 à 12:24

Je n'ai pas encore fait intégration en maths

Posté par
beuggre : Cinématique 2 04-12-16 à 12:25

Je ne comprends bien !

Posté par
diracre : Cinématique 2 04-12-16 à 12:41

Aïe ... je suis un peu sec

Cet exercice t'a t il été donné par ton prof?
Dans quel chapitre?
Quel est votre manuel de cours?
La dérivation t'est elle familière?

j'ai besoin de comprendre comment t'aider efficacement. Peut être des sachants de ce beau corps des enseignants peuvent ils venir à la rescousse.

Posté par
beuggre : Cinématique 2 04-12-16 à 13:16

Oui il a été donné par mon prof
C'est Cinématique du point matériel

Posté par
beuggre : Cinématique 2 04-12-16 à 13:48

Bon
Pour la question 1 , y= -x2-4x

Alors Q2:

On peut dire x [0, 2,5] , y= -x2-4x

y'=-x2-4x

C'est bon !

Posté par
beuggre : Cinématique 2 04-12-16 à 13:49

Oups !!

y'= -2x -4

Posté par
beuggre : Cinématique 2 04-12-16 à 13:51

beugg @ 04-12-2016 à 13:48

Bon
Pour la question 1 , y= -x2-4x

Alors Q2:

On peut dire t [0, 2,5] , y= -2x-4

y'=-x2-4x

C'est bon !

Posté par
beuggre : Cinématique 2 04-12-16 à 13:54

Pardon je ne fais pas attention

beugg @ 04-12-2016 à 13:48

Bon
Pour la question 1 , y= -x2-4x

Alors Q2:

On peut dire t[ smb]appartient[/smb] [0, 2,5] , y= -x2-4x

y'=-2x-4

Posté par
diracre : Cinématique 2 04-12-16 à 14:55

Je reprends

L'énoncé te dit que    \vec{a}(t) = -8.\vec{j}  ,  donc:

\\ \ddot{x}(t) = 0 \\ \ddot{y}(t) = -8   \\

La fonction de t  dont la dérivée est nulle est une fonction constante,
Donc si   \ddot{x}(t) = 0   alors     \dot{x}(t) = Cste1
(pour t'en convaincre, dérive   \dot{x}(t) )

La fonction de t dont la dérivée est une constante est une fonction affine de cette variable t:
Donc si   \ddot{y}(t) = -8   alors   \dot{y}(t) = -8 t + Cste2
(pour t'en convaincre, dérive   \dot{y}(t) )

Cste1 et Cste2 sont données par les conditions initiales de l'énoncé :    \vec{V}(t=0) = 2.\vec{i}  + 4.\vec{j}  

On a donc:

\\ \dot{x}(t=0) = Cste1= 2 \\ \\ \dot{y}(t=0) = -8 \times0 + Cste2 =4  

Donc  

\\ \dot{x}(t) = 2 \\ \\ \dot{y}(t) = -8 t + 4      soit     \vec{v}(t) = 2.\vec{i}  + (4-8t).\vec{j}   \\

Comme plus haut:
La fonction de t dont la dérivée est une constante est une fonction affine de cette variable t:
Donc si   \dot{x}(t) = 2    alors   x(t) = 2t + Cste3
(pour t'en convaincre, dérive   x(t) )

La fonction de t dont la dérivée est une fonction afine (polynôme du 1er degré)  est un polynôme du 2nd degré de cette variable t:
Donc si  \dot{y}(t) = -8 t + 4     alors   y(t) = -4t^2 + 4t + Cste4
(pour t'en convaincre, dérive   y(t) )

Cste3 et Cste4 sont données par les conditions initiales de l'énoncé :    \vec{OM}(t=0) = -3.\vec{i}  + 3.\vec{j}  

On a donc:

\\ x(t=0) = Cste3 = -3 \\ \\ y(t=0) = Cste4 =3  

En final:

x(t) = 2t  - 3
y(t) = -4t^2 + 4t + 3  

\vec{OM} = (2t-3)\vec{i}.  + (-4t^2+4t+3).\vec{j}

Pour trouver l'équation cartésienne il faut éliminer la variable t:

x = 2t  - 3   donc  t = \frac{1}{2}(x+3)

Et alors:

y(t) = -(x+3)^2 + 2(x+3) + 3 = -x^2 - 4x   

As tu compris?

Ensuite, tu ne donnes pas la question 2/ donc, difficile de t'aider.

Posté par
beuggre : Cinématique 2 04-12-16 à 18:49

Oui j'ai bien compris !
Vous avez très bien expliqué les choses !!Merci

Ensuite , pour la question 2, merci de guider ...

Posté par
diracre : Cinématique 2 04-12-16 à 19:06

Je veux bien, mais quelle est la question 2/?

Citation :
2/ 0 s  t  2,5 s


C'est un peu laconique ...  

Posté par
beuggre : Cinématique 2 04-12-16 à 19:13

Attension !!

Je viens de constater que on a fait une erreur de frappe pour la question 2
-----------------

2/ Representer la courbe pour :

0 s t 2,5 s

Je suis désolé !!

Posté par
beuggre : Cinématique 2 04-12-16 à 19:16

Bien sûr
y'= -2x -4

Posté par
diracre : Cinématique 2 04-12-16 à 19:30

On avait trouvé

y = -x^2 - 4x  

Tu as peut être une calculatrice graphique (moi j'ai une HP-15C   )

Tu dois trouver une portion de parabole entre les points

pour t = 0    M_0 (-3,3)
pour t = 2,5s  M_{2,5}(2,-12)

avec un sommet pour x = -2  (et donc y = 4   et  t = 0,5 s)

Posté par
beuggre : Cinématique 2 04-12-16 à 20:38

Oui
y est dérivable sur R ,en particulier  [-3, 2]

Posté par
beuggre : Cinématique 2 04-12-16 à 20:49

Pour t dans [0, 2,5],

x est dans [-3, 2]

Posté par
beuggre : Cinématique 2 04-12-16 à 20:51

Si vous me permettez je reviendrais à la suite demain

Bonne soirée donc dirac

Posté par
beuggre : Cinématique 2 05-12-16 à 20:06

Bonsoir

Je suis à la question 4:
Calculer la vitesse moyenne.
J'ai trouvé

V_m=\frac{|3,16-4,24|}{1-0}= 1,1 m/s

C'est bon ?

Posté par
beuggre : Cinématique 2 05-12-16 à 20:59

J'espère avoir votre réponse ce soir

Posté par
diracre : Cinématique 2 05-12-16 à 21:20

Hello

Peux tu justifier ton calcul numérique? Je n'arrive pas à l'associer à une méthode.
(Bon, là je prends le train, on va qd même essayer de faire avancer le sujet).

Posté par
beuggre : Cinématique 2 05-12-16 à 21:37

Ok

À t= 0 , x= -3 ; y= 3 ==>

d1= V18= 4,24 m

t=1,

x=-1 ; y=3

d2= 3,16 m

Posté par
diracre : Cinématique 2 05-12-16 à 22:06

Hum hum... tu ne peux pas calculer la distance parcourue comme la différence des 2 distances à l'origine. Il faut calculer/estimer la distance parcourue sur l'arc de la parabole! Le calcul par intégration de ds/dt me semble hors programme de la terminale. Peux être peux tu l'estimer?

Posté par
beuggre : Cinématique 2 05-12-16 à 22:46

Non et je n'ai pas encore fait l'intégration en maths

Posté par
diracre : Cinématique 2 05-12-16 à 23:14

Bon, ça m'arrange (je ne connais pas par coeur la  longueur d'une portion de parabole).

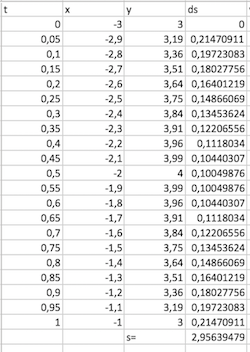
Donc je te propose d'estimer la distance parcourue le long de la parabole entre M_{t=0}(-3;3)  et  M_{t=1}(-1;3) décomposant la trajectoire en segment, toutes les 0,05 s.

ds étant calculé comme:   ds = \sqrt{\Delta x^2+\Delta y^2}

On trouve  s \approx 2,96  m distance parcourue entre t=0 s et t=1 s

Tu a donc v_{moy} = 2,96  m.s^{-1} (je viens de trouver une ligne de ton énoncé qui parle d'unité de longueur, ouf! ça allait m'agacer)

A noter:
1) qu'il n'est pas "rentable" diminuer le pas de temps dans les échantillons (un pas de 0,01 s donne 2,9578 vs 2,9564 dans le tableau ci dessous)
2) peut être que ta calculatrice ou bien des logiciels type "geogebra" sont capables de fournir le résultat sans passer par un tableur
3) bonne nouvelle: l'accélération moyenne devrait aller plus vite ...

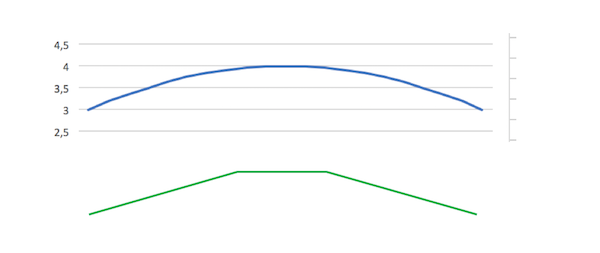
Cinématique 2

Posté par
diracre : Cinématique 2 05-12-16 à 23:23

Je me demande même si, en utilisant ta représentation graphique, et en "l'approximant" avec 2 ou 3 segments, tu ne trouves pas en trois mesures, une estimée de s tout à fait honnête.

Cinématique 2

Posté par
beuggre : Cinématique 2 06-12-16 à 08:19

Merci

Donc am= 2/1 = 2 m/s2

Posté par
beuggre : Cinématique 2 06-12-16 à 08:21

am= \vec{V}/t

Posté par
diracre : Cinématique 2 06-12-16 à 09:19

Hello

Je reviens juste une seconde sur la question précédente du calcul de la vitesse moyenne (je m'attendais à bien plus de questions de ta part).
Juste "pour la beauté du geste", la distance exacte parcourue durant la 1ere seconde est:

s : \int_0^1\sqrt{4 + (4-8t)^2}.dt = \sqrt{5} + \frac{Argsh(2)}{2} \approx 2,9579 m

Je referme ici la parenthèse. Et revenons à:

Citation :
En déduire l'accélération moyenne entre ces mêmes instants.


Première remarque:

Citation :
a_m= \Delta\vec{V}/\Delta t

A gauche du signe = tu as un réel, à droite un vecteur ...  pas beau

Deuxième remarque:

a_m= \Delta{v}/\Delta t est effectivement une définition de l'accélération moyenne. Mais attention, le mouvement n'est pas linéraire, il te faut donc moyenner les composantes de l'accélération:
tv_xv_y
024
12-4


Donc
a_{m,x} = \frac{v_x(t=1) - v_x(t=0)}{1 - 0} = 0 m.s^{-2}
a_{m,y} = \frac{v_y(t=1) - v_y(t=0)}{1 - 0} = -8 m.s^{-2}

Donc
a_m = - 8 m.s^{-2}

Et c'est heureux car il est écrit dans l'énoncé que l'accélération était à tout instant:
Citation :
un vecteur accélération \vect{a}= -8\vec{j}


Ce qui amène ma 3ème remarque:

Le "en déduire (de la vitesse moyenne) l'expression de l'accélération moyenne" me semble  saugrenu, à moins que je n'ai pas perçu le propos de l'exercice bien sûr

Posté par
beuggre : Cinématique 2 06-12-16 à 09:25

Sinon ,le reste je pense que j'ai compris

Sauf j'avais une question particulière que je voudrais poser à la fin :

La question est la suivante :
Dans les conditions initiales x ou y ... ne dépendent pas de t
Par exemple pour la position de M0,on x= -3 ; y= 3

Non x= -3t ; y= 3t


Merci de m'expliquer

Posté par
beuggre : Cinématique 2 06-12-16 à 09:26

Oups !! Désolé
Je n'avais pas vu la suite

Posté par
diracre : Cinématique 2 06-12-16 à 09:40

J'ai RIEN compris à ta question ...

Citation :
Dans les conditions initiales x ou y ... ne dépendent pas de t


Les conditions initiales donnent les valeurs de x et y à un instant précis: t = 0,

Soit f(t) = 2t + 1 par exemple

La condition initiale c'est f(0), souvent noté  f(t=0) donc c'est 1

Posté par
beuggre : Cinématique 2 06-12-16 à 09:53

"Je m'attendais à bien plus de questions de ta part "

Oui parce que je voulais pas entrer pour le moment sur les détails de formule utilisée pour calculer s exactement

Ok de toute façon j'ai compris

Et vous avez fait une bonne fin de réussir votre aide précieuse en donnant la belle valeur de am

Posté par
beuggre : Cinématique 2 06-12-16 à 09:54

Les messages se croisent ...

Posté par
diracre : Cinématique 2 06-12-16 à 10:09

Tout va bien alors.

Pour calculer les accélérations normale et tangentielle à t = 0,5 s,  il serait judicieux de t'inspirer de ce que tu as déjà fait dans ton exercice "Cinématique 1"

Posté par
beuggre : Cinématique 2 06-12-16 à 10:17

Oui tout à fait

Merci beaucoup dirac de votre aide

À bientôt

Posté par
diracre : Cinématique 2 06-12-16 à 10:20

Excuse moi, je suis stupide ...

t = 0,5 s est un moment particulier de la trajectoire:  c'est le sommet de la parabole.  aT et aN se trouvent donc immédiatement (ie sans caulcul aucun)


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 237 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !